1、平衡二叉树
它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。　
如图：

2、动态平衡技术
动态平衡技术
Adelson-Velskii 和 Landis 提出了一个动态地保持二叉排序树平衡的方法，其基本思想是：
　　在构造二叉排序树的过程中，每当插入一个结点时，首先检查是否因插入而破坏了树的平衡性，如果是因插入结点而破坏了树的平衡性，则找出其中最小不平衡子树，在保持排序树特性的前提下，调整最小不平衡子树中各结点之间的连接关系，以达到新的平衡。通常将这样得到的平衡二叉排序树简称为 AVL 树。
那么什么是 最小不平衡子树
　　以离插入结点最近、且平衡因子绝对值大于 1 的结点作根结点的子树。为了简化讨论，不妨假设二叉排序树的最小不平衡子树的根结点为 A ，则调整该子树的规律可归纳为下列四种情况：
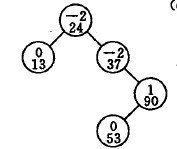
如图：当插入结点为53时，结点37则为最小不平衡子树 A
单向
（1） LL 型：（单向右旋）
原因是：在A的左子树插入左子树，导致A平衡恩子为2，失去平衡。需要向右旋转一次、
　　新结点 X 插在 A 的左孩子的左子树里。调整方法见图 8.5(a) 。图中以 B 为轴心，将 A 结点从 B 的右上方转到 B 的右下侧，使 A 成为 B 的右孩子。


（2）RR 型：（单向向左旋）
同上。则是方向变了右
　　新结点 X 插在 A 的右孩子的右子树里。调整方法见图 8.5(b) 。图中以 B 为轴心，将 A 结点从 B 的左上方转到 B 的左下侧，使 A 成为 B 的左孩子。



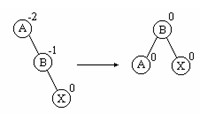
双向：
（3）LR 型：（先左后右）
　　新结点 X 插在 A 的左孩子的右子树里。调整方法见图 8.5(c) 。分为两步进行：第一步以 X 为轴心，将 B 从 X 的左上方转到 X 的左下侧，使 B 成为 X 的左孩子， X 成为 A 的左孩子。第二步跟 LL 型一样处理 ( 应以 X 为轴心 ) 。 
//此时大小是 B<X<A 那么应该将中间的那个X做根结点
（4）RL 型：（先右后左）
　　新结点 X 插在 A 的右孩子的左子树里。调整方法见图 8.5(d) 。分为两步进行：第一步以 X 为轴心，将 B 从 X 的右上方转到 X 的右下侧，使 B 成为 X 的右孩子， X 成为 A 的右孩子。第二步跟 RR 型一样处理 ( 应以 X 为轴心

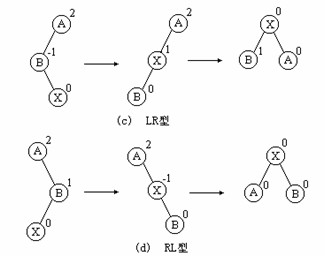
【例】
实际的插入情况，可能比图 8.5 要复杂。因为 A 、 B 结点可能还会有子树。现举一例说明，设一组记录的关键字按以下次序进行插入： 4 、 5 、 7 ， 2 、 1 、 3 、 6 ，其生成及调整成二叉平衡树的过程示于图 8.6 。
　　在图 8.6 中，当插入关键字为 3 的结点后，由于离结点 3 最近的平衡因子为 2 的祖先是根结点 5 。所以，第一次旋转应以结点 4 为轴心，把结点 2 从结点 4 的左上方转到左下侧，从而结点 5 的左孩子是结点 4 ，结点 4 的左孩子是结点 2 ，原结点 4 的左孩子变成了结点 2 的右孩子。第二步再以结点 4 为轴心，按 LL 类型进行转换。这种插入与调整平衡的方法可以编成算法和程序，这里就不再讨论了。

         图 8.6 二叉平衡树插入结点 ( 结点旁的数字为其平衡因子 )

代码实

/*

    数据结构C语言版平衡二叉树

    P236

    编译环境：Dev-C++ 4.9.9.2

    日期：2011年2月15日

*/

 

#include <stdio.h>

#include <malloc.h>

 

#define LH +1   // 左高

#define EH 0    // 等高

#define RH -1   // 右高

#define N 5     // 数据元素个数

 

typedef char KeyType; // 设关键字域为字符型

 

typedef struct

{

    KeyType key;

    int order;

}ElemType; // 数据元素类型

 

// 平衡二叉树的类型

typedef struct BSTNode

{

    ElemType data;

    // bf结点的平衡因子,只能够取0，-1，1，它是左子树的深度减去

    // 右子树的深度得到的

    int bf;

    struct BSTNode *lchild,*rchild; // 左、右孩子指针

}BSTNode,*BSTree;

 

// 构造一个空的动态查找表DT

int InitDSTable(BSTree *DT)

{

    *DT=NULL;

    return 1;

}

 

// 销毁动态查找表DT

void DestroyDSTable(BSTree *DT)

{

    if(*DT) // 非空树

    {

        if((*DT)->lchild) // 有左孩子

            DestroyDSTable(&(*DT)->lchild); // 销毁左孩子子树

        if((*DT)->rchild) // 有右孩子

            DestroyDSTable(&(*DT)->rchild); // 销毁右孩子子树

        free(*DT); // 释放根结点

        *DT=NULL; // 空指针赋0

    }

}

 

// 算法9.5(a) 

// 在根指针T所指二叉排序树中递归地查找某关键字等于key的数据元素，

// 若查找成功，则返回指向该数据元素结点的指针,否则返回空指针。
//同二叉排序树的查找算法

BSTree SearchBST(BSTree T,KeyType key)

{

    if((!T)|| (key == T->data.key))

        return T; // 查找结束

    else if(key < T->data.key) // 在左子树中继续查找

        return SearchBST(T->lchild,key);

    else

        return SearchBST(T->rchild,key); // 在右子树中继续查找

}

 

// 算法9.9 P236

// 对以*p为根的二叉排序树作右旋处理 ，处理之后p指向新的树根结点，即旋转

// 处理之前的左子树的根结点。

void R_Rotate(BSTree *p)

{

    BSTree lc;

    lc=(*p)->lchild; // lc指向p的左子树根结点

    (*p)->lchild=lc->rchild; // lc的右子树挂接为p的左子树

    lc->rchild=*p;

    *p=lc; // p指向新的根结点

}

 

// 算法9.10  P236

// 对以*p为根的二叉排序树作左旋处理 ，处理之后p指向新的树根结点，即旋转

// 处理之前的右子树的根结点。

void L_Rotate(BSTree *p)

{

    BSTree rc;

    rc=(*p)->rchild; // rc指向p的右子树根结点

    (*p)->rchild=rc->lchild; // rc的左子树挂接为p的右子树

    rc->lchild=*p;

    *p=rc; // p指向新的根结点

}

 

// 算法9.12 P238

// 对以指针T所指结点为根的二叉树作左平衡旋转处理，本算法结束时，

// 指针T指向新的根结点。

void LeftBalance(BSTree *T)

{  

    BSTree lc,rd;

    lc=(*T)->lchild; // lc指向*T的左子树根结点

    switch(lc->bf)

    { // 检查*T的左子树的平衡度，并作相应平衡处理

    case LH: // 新结点插入在*T的左孩子的左子树上，要作单右旋处理

        (*T)->bf=lc->bf=EH;

        R_Rotate(T);

        break;

    case RH: // 新结点插入在*T的左孩子的右子树上，要作双旋处理

        rd=lc->rchild; // rd指向*T的左孩子的右子树根

        switch(rd->bf)

        { // 修改*T及其左孩子的平衡因子

        case LH:

            (*T)->bf=RH;

            lc->bf=EH;

            break;

        case EH:

            (*T)->bf=lc->bf=EH;

            break;

        case RH:

            (*T)->bf=EH;

            lc->bf=LH;

        }

        rd->bf=EH;

        L_Rotate(&(*T)->lchild); // 对*T的左子树作左旋平衡处理

        R_Rotate(T); // 对*T作右旋平衡处理

    }

}

 

// 对以指针T所指结点为根的二叉树作右平衡旋转处理，本算法结束时，

// 指针T指向新的根结点

void RightBalance(BSTree *T)

{

    BSTree rc,rd;

    rc=(*T)->rchild; // rc指向*T的右子树根结点

    switch(rc->bf)

    { // 检查*T的右子树的平衡度，并作相应平衡处理

    case RH: // 新结点插入在*T的右孩子的右子树上，要作单左旋处理

        (*T)->bf=rc->bf=EH;

        L_Rotate(T);

        break;

    case LH: // 新结点插入在*T的右孩子的左子树上，要作双旋处理

        rd=rc->lchild; // rd指向*T的右孩子的左子树根

        switch(rd->bf)

        { // 修改*T及其右孩子的平衡因子

        case RH: (*T)->bf=LH;

            rc->bf=EH;

            break;

        case EH: (*T)->bf=rc->bf=EH;

            break;

        case LH: (*T)->bf=EH;

            rc->bf=RH;

        }

        rd->bf=EH;

        R_Rotate(&(*T)->rchild); // 对*T的右子树作右旋平衡处理

        L_Rotate(T); // 对*T作左旋平衡处理

    }

}

 

// 算法9.11

// 若在平衡的二叉排序树T中不存在和e有相同关键字的结点，则插入一个

// 数据元素为e的新结点，并返回1，否则返回0。若因插入而使二叉排序树

// 失去平衡，则作平衡旋转处理，布尔变量taller反映T长高与否。

int InsertAVL(BSTree *T,ElemType e,int *taller)

{

    if(!*T)

    { // 插入新结点，树“长高”，置taller为1

        *T=(BSTree)malloc(sizeof(BSTNode));

        (*T)->data=e;

        (*T)->lchild=(*T)->rchild=NULL;

        (*T)->bf=EH;

        *taller=1;

    }

    else

    {

        if(e.key == (*T)->data.key)

        { // 树中已存在和e有相同关键字的结点则不再插入

            *taller=0;

            return 0;

        }

        if(e.key < (*T)->data.key)

        { // 应继续在*T的左子树中进行搜索

            if(!InsertAVL(&(*T)->lchild,e,taller)) // 未插入

                return 0;

            if(*taller)

                //  已插入到*T的左子树中且左子树“长高”

                switch((*T)->bf) // 检查*T的平衡度

                {

                case LH:

                    // 原本左子树比右子树高，需要作左平衡处理

                    LeftBalance(T);

                    *taller=0;  //标志没长高

                    break;

                case EH:

                    // 原本左、右子树等高，现因左子树增高而使树增高

                    (*T)->bf=LH;

                    *taller=1;  //标志长高

                    break;

                case RH:

                    // 原本右子树比左子树高，现左、右子树等高

                    (*T)->bf=EH;

                    *taller=0;  //标志没长高

            }

        }

        else

        {

            // 应继续在*T的右子树中进行搜索

            if(!InsertAVL(&(*T)->rchild,e,taller)) // 未插入

                return 0;

            if(*taller) // 已插入到T的右子树且右子树“长高”

                switch((*T)->bf) // 检查T的平衡度

            {

           case LH:

               (*T)->bf=EH; // 原本左子树比右子树高，现左、右子树等高

               *taller=0;

               break;

           case EH: // 原本左、右子树等高，现因右子树增高而使树增高

               (*T)->bf=RH;

               *taller=1;

               break;

           case RH: // 原本右子树比左子树高，需要作右平衡处理

               RightBalance(T);

               *taller=0;

            }

        }

    }

    return 1;

}

 

// 按关键字的顺序对DT的每个结点调用函数Visit()一次

void TraverseDSTable(BSTree DT,void(*Visit)(ElemType))

{

    if(DT)

    {

        TraverseDSTable(DT->lchild,Visit); // 先中序遍历左子树

        Visit(DT->data); // 再访问根结点

        TraverseDSTable(DT->rchild,Visit); // 最后中序遍历右子树

    }

}

 

 

void print(ElemType c)

{

    printf("(%d,%d)",c.key,c.order);

}

 
测试

int main()

{

    BSTree dt,p;

    int k;

    int i;

    KeyType j;

    ElemType r[N]={

        {13,1},{24,2},{37,3},{90,4},{53,5}

    }; // (以教科书P234图9.12为例)

   

    InitDSTable(&dt);   // 初始化空树

    for(i=0;i<N;i++)

        InsertAVL(&dt,r[i],&k); // 建平衡二叉树

    TraverseDSTable(dt,print); // 按关键字顺序遍历二叉树

    printf("\n请输入待查找的关键字: ");

    scanf("%d",&j);

    p=SearchBST(dt,j); // 查找给定关键字的记录

    if(p)

        print(p->data);

    else

        printf("表中不存在此值");

    printf("\n");

    DestroyDSTable(&dt);

   

    system("pause");

    return 0;

}

/*

输出效果：

 

(13,1)(24,2)(37,3)(53,5)(90,4)

请输入待查找的关键字: 53

(53,5)

请按任意键继续. . .。（参考）

/////////////////////////待续。