题目描述：

你是山西的一个煤老板，你在矿区开采了有3000吨煤需要运送到市场上去卖，从你的矿区
到市场有1000公里，你手里有一列烧煤的火车，这个火车最多只能装1000吨煤，且其能耗比较大——每一公里需要耗一吨煤。请问，作为一个懂编程的煤老板的你，你会怎么运送
才能运最多的煤到集市？

下面我想阐述下我的思考过程：

确实是个好题，我开始没想到好办法，就开始试了几组数据，大概的思路应该和大家的差不多： 就是设两个中转站，如下图所示：

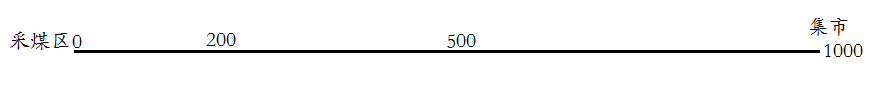
第一次尝试：

具体的过程是这样的：

第一趟： 从采煤区运1000吨煤到200公里处，这时消耗掉200吨，留下600吨，后携带200吨返回。

第二趟： 从采煤区运1000吨煤到200公里处，这时消耗200吨，但是我们增加200吨，这时200公里处剩下400吨，然后继续前行到达500公里处，卸下400吨后返回，在200公里处在添加200吨煤，后返回到采煤区。

第三趟： 从采煤区1000吨煤到200公里处，增加200吨煤，然后继续前行到500这个地方，这时我们的列车上还有700吨煤，我们添加300吨继续前行到集市，我们这时还剩500吨。

所以运送到集市为500吨。

但是我们发现有100吨煤在500公里还没用，说明还有改进空间。

第二次尝试：

但是我发现200公里处是最优的，所以我假设我们需要两个中转站： x1公里处， x2公里处；同时我们令：x1 = 200;

我们按照上面的过程继续 f1 表示x1的剩余量， f2表示 x2的剩余量；

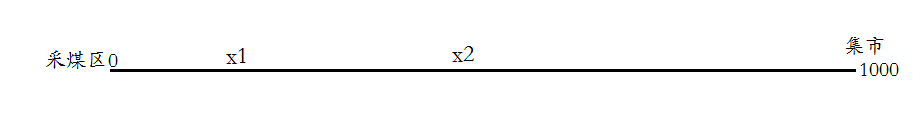
第一趟： f1  =  1000 - 2 * x1; f2  =  0;

第二趟： f1  = 1000 - 4 * x1; f2 =  1000 - 2* (x2-x1);

第三趟： f1 =  1000 - 5 * x1; f2 = 1000 - 2*(x2 – x1) + 1000 – (x2 – x1);

我们发现： 当我们把x1 = 200带入得到： f1 = 0; f2 = 2600 – 3*x2;

我们假设我们取其中的f3 但是f3 <= 1000

最后的载运量令为f = f3 – (1000 – x2);  

所以我们令f3 = 1000 得到f = 1600/3; 最优值大概是533.333…..

故事还没结束：。。。。。

但是我们还没发现完里面的玄机：我们发现 1600/3 – 200 = 1000/3;

这是偶然吗，哦NO, 继续 200 = 1000/5，

我们发现0-----x1 火车经过5次， x1 ----x2火车经过3次， 这是偶然吗，当然不是

现在思考整个过程：1000吨在0 ---x1消耗的，需要5次， 同理1000吨是在x1----x2消耗，需要3次。

现在明白了吧其实结果就是1000/5 + 1000/3;

假设现在是4000吨煤呢： 道理很显然了吧 1000/7 + 1000/5 + 1000/3

如果是一般情况呢： n*1000    (n>=2), 显然n = 1 时答案为0

这个结果就是 1000 * (1/3 + 1/5 + 1/7 + ….. + 1 / (2*n-1)), 查了下这是个发散的级数，所以还是比较符合现实规律的， 煤假设是无穷的，那么运的也应该是无穷的。

不知道存在问题不， 希望大家给出