两点间的最短路径,SPFA算法求单源最短路径可得。 当然用Dijkstra或Bellman_Ford也是可以的。
SPFA算法简介
SPFA算法采用图的存储结构是邻接表,方法是动态优化逼近法。算法中设立了一个先进先出的队列Queue用来保存待优化的顶点,优化时从此队列里顺序取出一个点w,并且用w点的当前路径D[W]去优化调整其它各点的路径值D[j],若有调整,即D[j]的值改小了,就将J点放入Queue队列以待继续进一步优化。反复从Queue队列里取出点来对当前最短路径进行优化,直至队空不需要再优化为止,此时D数组里就保存了从源点到各点的最短路径值 。
下面举一个实例来说明SFFA算法是怎样进行的:
设有一个有向图G={V,E},其中,V={V0,V1,V2,V3,V4},E={<V0,V1>,<V0,V4>,<V1,V2>,<V1,V4>,<V2,V3>,<V3,V4>,<V4,V2>}={2,10,3,7,4,5,6},见下图:
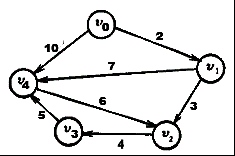
算法执行时各步的Queue队的值和D数组的值由下表所示。
表一 实例图SPFA算法执行的步骤及结果
|
初始
|
第一步
|
第二步
|
第三步
|
第四步
|
第五步
|
|
queue
|
D
|
queue
|
D
|
queue
|
D
|
queue
|
D
|
queue
|
D
|
queue
|
D
|
|
V0
|
0
|
V1
|
0
|
V4
|
0
|
V2
|
0
|
V3
|
0
|
|
0
|
|
∞
|
V4
|
2
|
V2
|
2
|
|
2
|
|
2
|
|
2
|
|
∞
|
|
∞
|
|
5
|
|
5
|
|
5
|
|
5
|
|
∞
|
|
∞
|
|
∞
|
|
∞
|
|
9
|
|
9
|
| |
∞
|
|
10
|
|
9
|
|
9
|
|
9
|
|
9
|
算法执行到第五步后,队Queue空,算法结束。源点V0到V1的最短路径为2,到V2的最短路径为5,到V3的最短路径为9,到V4的最短路径为9,结果显然是正确的。

 本题源代码
本题源代码
1 #include<iostream>
#include<iostream>
2 #include<queue>
#include<queue>
3
4 using namespace std;
using namespace std;
5
6 const int MAXN = 1001;
const int MAXN = 1001;
7 const int INF = 1000*100; //每条边长的范围为1-100,故路径总长上界为999*100 + 1,直接用1000*100省事
const int INF = 1000*100; //每条边长的范围为1-100,故路径总长上界为999*100 + 1,直接用1000*100省事
8
9 int G[MAXN][MAXN];
int G[MAXN][MAXN];
10
11 int SPFA(int n) //SPFA算法求单源最短路径
int SPFA(int n) //SPFA算法求单源最短路径
12

 {
{
13 int d[MAXN];
int d[MAXN];
14 bool visited[MAXN];
bool visited[MAXN];
15 queue<int> q;
queue<int> q;
16 int v;
int v;
17
18 for(int i=1; i<=n; i++)
for(int i=1; i<=n; i++)
19

 {
{
20 d[i] = INF;
d[i] = INF;
21 visited[i] = false;
visited[i] = false;
22 }
}
23 d[1] = 0;
d[1] = 0;
24 visited[1] = true;
visited[1] = true;
25 q.push(1);
q.push(1);
26
27 while(!q.empty())
while(!q.empty())
28

 {
{
29 v = q.front();
v = q.front();
30 visited[v] = false;
visited[v] = false;
31 q.pop();
q.pop();
32
33 for(int i=1; i<=n; i++)
for(int i=1; i<=n; i++)
34

 {
{
35 if(d[i] > d[v] + G[v][i])
if(d[i] > d[v] + G[v][i])
36

 {
{
37 d[i] = d[v] + G[v][i];
d[i] = d[v] + G[v][i];
38 if(!visited[i])
if(!visited[i])
39

 {
{
40 q.push(i);
q.push(i);
41 visited[i] = true;
visited[i] = true;
42 }
}
43 }
}
44 }
}
45 }
}
46 return d[n];
return d[n];
47 }
}
48
49 int main()
int main()
50

 {
{
51 int T,N;
int T,N;
52 int a,b,c;
int a,b,c;
53
54 int i,j;
int i,j;
55
56 while(cin>>T>>N)
while(cin>>T>>N)
57

 {
{
58 for(i=1; i<=N; i++)
for(i=1; i<=N; i++)
59

 {
{
60 for(j=1; j<=N; j++)
for(j=1; j<=N; j++)
61

 {
{
62 G[i][j] = INF;
G[i][j] = INF;
63 }
}
64 }
}
65
66 for(i=1; i<=T; i++)
for(i=1; i<=T; i++)
67

 {
{
68 cin>>a>>b>>c;
cin>>a>>b>>c;
69 if(G[a][b] > c) //注意,有重边
if(G[a][b] > c) //注意,有重边
70

 {
{
71 G[a][b] = c;
G[a][b] = c;
72 G[b][a] = c;
G[b][a] = c;
73 }
}
74 }
}
75
76 cout<<SPFA(N)<<endl;
cout<<SPFA(N)<<endl;
77 }
}
78 return 0;
return 0;
79 }
}