1. 睿睿的随机数(Rating:easy)
输入文件名“radom.in” 输出文件名“estdout.pc2”
睿睿想在学校中请一些同学一起做一项问卷调查,为了实验的客观性,他先用计算机生成了N个1到1000之间的随机整数(N≤100),对于其中重复的数字,只保留一个,把其余相同的数去掉,不同的数对应着不同的学生的学号。然后再把这些数从小到大排序,按照排好的顺序去找同学做调查。请你协助睿睿完成“去重”与“排序”的工作。
输入格式
输入文件有2行,第1行为1个正整数,表示所生成的随机数的个数:N
第2行有N个用空格隔开的正整数,为所产生的随机数。
输出格式
输出文件也是2行,第1行为1个正整数M,表示不相同的随机数的个数。第2行为M个用空格隔的正整数,为从小到大排好序的不相同的随机数。
输入样本
10
20 40 32 67 40 20 89 300 400 15
输出样本
8
15 20 32 40 67 89 300 400
2. 国家利益(Rating:
medium-easy)
没有永远的朋友,也没有永远的敌人,国家的行为取决于国家利益,国家的地位取决于国家实力。伊拉克战争结束后N个国家正在联合国开会商讨如何分配伊拉克的M块油田。
N个国家按国家实力编号1,2,3...N,1号国家实力最强,第一个发言,N号最后一个发言;依次类推发言国家会提出一个分配方案,所有有表决权的国家进行表决(包括发言国家自己);如果50%或以上同意此方案,则会议结束,按照此国的方案分配油田,否则该国丧失表决权,下个国家重复上述过程。那么第一个国家提出怎样的方案才能使本国利益最大化?
提示:
每个国家分得的油田都是整数,不会出现几个国家共同拥有一块油田
每个国家都不希望别人的方案通过,但是每个国家都按照本国利益投票,比如1号国家提出一个方案, X号国家分Y油田,X号国家会进行比较, 如果该方案被否决,那么下次2号提出的方案X号国家分Z油田,而Z < Y,那么X号国家会赞成1号的方案, 否则反对
输入格式
输入文件有由若干行构成,每行包括一组数据由2个整数N,M构成,(N,M <= 10^8),输入文件的最后一行是‘#’表示文件结束。
输出格式
按照输入文件的顺序对于每组输入数据输出一行,每行包括1个整数,1号国家能获得的最多油田数。
Sample Input
7 100
6 100
#
Sample Output
97
98
3.Base64 编码 (Rating: medium)
Base64编码用来将任意的八位字节序列表示成为区分大小写的让人难以理解的形式。Base64编码用到了US-ASCII中的一个有65个元素的子集,能表示出可打印字符的其中6位。(额外的第65个字符‘=’,用来做特殊处理)。
编码过程中,将一个24位的输入作为一个整体,处理成4个字符输出。编码从左向右进行,一个24位的输入是由三个连续的8位字节组成,这些24位被看成是4个连续的6位的正整数,每一个正整数都被转换成Base64字符表中的一个数字。每个6位的正整数都是64个字符数组的地址。由此地址确定的字符将会放到输出字符串。
Table
1: Base 64 字符表
值 编码 值 编码 值 编码 值 编码
0
A 17 R 34 i 51 z
1 B 18 S 35 j 52 0
2
C 19 T 36 k 53 1
3 D 20 U 37 l
54 2
4 E 21 V 38 m
55 3
5
F 22 W 39 n 56 4
6
G 23 X 40 o 57 5
7 H 24 Y 41 p 58 6
8 I 25 Z 42 q 59 7
9 J 26 a
43 r 60 8
10 K 27 b 44 s 61 9
11 L 28 c 45 t 62 +
12 M
29 d 46 u 63 /
13 N 30 e 47 v
14 O 31 f 48 w (pad) =
15 P 32 g
49 x
16 Q 33 h 50 y
当输入数据的最后少于24bit的时候就需要特殊处理,最后总是能完全编码。当输入串最后少于24位的时候,不足的部分补0。填充的数据用 ‘=’ 来编码,由于所有的输入都是八位的字符,所以只有下列情况发生:
1、
最后剩余的bit数是24的倍数,输出的字符数目将是4的倍数,不会有 ’=’追加。
2、
最后剩余的 bit 数正好为 8 bits,此时在编码串后追加两个 ‘=’ 字符。
3、
最后剩余的 bit 数正好是 16bits,此时在编码串后追加一个 ‘=’ 字符
输入格式
第一行是一个正整数 T(1 <= T <= 100),表示数据的组数。接着是 T行,每一行为一个待编码的字符串。
输出格式
对于每一个测试用例,输出相应的编码字符串。
输入样本
4
What is
your name
i
you
yes
输出样本
V2hhdCBpcyB5b3VyIG5hbWU=
aQ==
eW91
eWVz
4.同色游戏 (Rating: medium)
N个学生排成一排,每个学生都穿着某一种颜色的服装。一共有m种颜色,因此每一种颜色都可以用0到m-1之间的一个数字表示。吴老师想让他的学生都只同一种颜色的衣服,
因此他需要一些操作。我们都知道吴老师是一个非常奇怪的人,如果某个学生穿着第i种颜色的衣服而且吴老师想让这个学生换别的颜色,他在一次操作中只让这个学生换成第(i+1)%m种颜色的服装。更加奇怪的是,吴老师总是让连续的t个学生一起改变他们服装的颜色。现在问题来了,我们给你参数n,m和t(n<2000,m<150,t<n),而且告诉你开始的时候各个学生服装的颜色,让你计算出最少需要多少次操作可以使得每个学生都穿同一种颜色的服装。
输入格式
在输入的第一行是k<=30,表示有多少组测试数据。
对于每一种测试数据,有三个输入数据,n,m,t.接着是一行n个数字ai (i=1,2…n), (0<=ai<=m-1).ai 表示第i个学生衣服的颜色。
输出格式
对于每一种测试数据,你需要在一行中输出两个数据,分别是所需要的最少的操作次数和最后学生衣服的颜色。如果有两种颜色可以通过相同的操作次数得到,你只需要输出较小数字所代表的颜色。题目保证对于所有的测试数据均可以通过某种操作使得所有的学生都穿同一种颜色的服装。
输入样本
1
7 2 3
0 0 1 0 1 0 0
输出样本
3 1
5 Is It A Tree? (Rating:
medium)
A tree is a well-known data structure that
is either empty (null, void, nothing) or is a set of one or more nodes
connected by directed edges between nodes satisfying the following properties.
1.
There is exactly one node, called the root, to which no directed edges point.
2.
Every node except the root has exactly one edge pointing to it.
3.
There is a unique sequence of directed edges from the root to each node.
For example, consider the illustrations
below, in which nodes are represented by circles and edges are represented by
lines with arrowheads. The first two of these are trees, but the last is not.
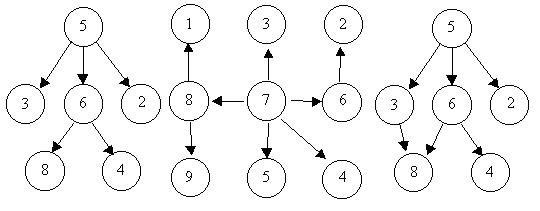
In this problem you will be given several
descriptions of collections of nodes connected by directed edges. For each of
these you are to determine if the collection satisfies the definition of a tree
or not.
Input
The input will consist of a sequence of
descriptions (test cases) followed by a pair of negative integers. Each test
case will consist of a sequence of edge descriptions followed by a pair of
zeroes Each edge description will consist of a pair of integers; the first
integer identifies the node from which the edge begins, and the second integer
identifies the node to which the edge is directed. Node numbers will always be
greater than zero.
Output
For each test case display the line
"Case k is a tree." or the line "Case k is not a tree.",
where k corresponds to the test case number (they are sequentially numbered
starting with 1).
Sample Input
6 8
5 3 5 2 6 4
5 6
0 0
8 1
7 3 6 2 8 9 7
5
7 4
7 8 7 6 0 0
3 8
6 8 6 4
5 3
5 6 5 2 0 0
-1 -1
Sample Output
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.
6. Coconuts, Revisited (Rating:
medium)
The short story titled Coconuts, by Ben
Ames Williams, appeared in the Saturday Evening Post on October 9, 1926. The
story tells about five men and a monkey who were shipwrecked on an island. They
spent the first night gathering coconuts. During the night, one man woke up and
decided to take his share of the coconuts. He divided them into five piles. One
coconut was left over so he gave it to the monkey, then hid his share and went
back to sheep.
Soon a second man woke up and did the same
thing. After dividing the coconuts into five piles, one coconut was left over
which he gave to the monkey. He then hid his share and went back to bed. The
third, fourth, and fifth man followed exactly the same procedure. The next
morning, after they all woke up, they divided the remaining coconuts into five
equal shares. This time no coconuts were left over.
An obvious question is "how many
coconuts did they originally gather?" There are an infinite number of
answers, but the lowest of these is 3,121. But that's not our problem here.
Suppose we turn the problem around. If we
know the number of coconuts that were gathered, what is the maximum number of
persons (and one monkey) that could have been shipwrecked if the same procedure
could occur?
Input
The input will consist of a sequence of
integers, each representing the number of coconuts gathered by a group of
persons (and a monkey) that were shipwrecked. The sequence will be followed by
a negative number.
Output
For each number of coconuts, determine the
largest number of persons who could have participated in the procedure
described above. Display the results similar to the manner shown below, in the
Expected Output. There may be no solution for some of the input cases; if so,
state that observation.
Sample Input
25
30
3121
-1
Sample Output
25 coconuts, 3 persons and 1 monkey
30 coconuts, no solution
3121 coconuts, 5 persons and 1 monkey
7. Transferable Voting (Rating:
medium-hard)
The Transferable Vote system for
determining the winner of an election requires that a successful candidate
obtain an absolute majority of the votes cast, even when there are more than
two candidates. To achieve this goal, each voter completes his or her ballot by
listing all the candidates in order of preference. Thus if there are five
candidates for a single position, each voter's ballot must contain five
choices, from first choice to fifth choice.
In this problem you are to determine the
winner, if any, of elections using the Transferable Vote system. If there are c
candidates for the single position, then each voter's ballot will include c
distinct choices, corresponding to identifying the voter's first place, second
place, ..., and nth place selections. Invalid ballots will be discarded, but
their presence will be noted. A ballot is invalid if a voter's choices are not
distinct (choosing the same candidate as first and second choice isn't
permitted) or if any of the choices aren't legal (that is, in the range 1 to
c).
For each election candidates will be
assigned sequential numbers starting with 1. The maximum number of voters in
this problem will be 100, and the maximum number of candidates will be 5.
Table A Table B
----------------------------- -------
Voter
First Second Third
Choice Choice Choice
1 1 2
4
2 1 3
2 1
3 2
3 3 2
1 3 2 1
4 3 2
1 3 2 1
5 1 2
3 1 2 3
6 2 3
1 3 1
7 3 2
1 3 2 1
8 3 1
1
9 3
2 1 3
2 1
10
1 2 3
1 2 3
11
1 3 2
1 3 2
12
2 3 1
3 1
Consider a very small election. In Table A
are the votes from the 12 voters for the three candidates. Voters 1 and 8 cast
invalid ballots; they will not be counted. This leaves 10 valid ballots, so a
winning candidate will require at least 6 votes (the least integer value
greater than half the number of valid ballots) to win. Candidates 1 and 3 each
have 4 first choice votes, and candidate 2 has two. There is no majority, so
the candidate with the fewest first choice votes, candidate 2, is eliminated.
If there had been several candidates with the fewest first choice votes, any of
them, selected at random, could be selected for elimination.
With candidate 2 eliminated, we advance the
second and third choice candidates from those voters who voted for candidate 2
as their first choice. The result of this action is shown in Table B. Now
candidate 3 has picked up 2 additional votes, giving a total of 6. This is
sufficient for election. Note that if voter 12 had cast the ballot "2 1
3" then there would have been a tie between candidates 1 and 3.
Input
There will be one or more elections to
consider. Each will begin with a line containing the number of candidates and
the number of voters, c and n. Data for the last election will be followed by a
line containing two zeroes.
Following the first line for each election
will be n additional lines each containing the choices from a single ballot.
Each line will contain only c non-negative integers separated by whitespace.
Output
For each election, print a line identifying
the election number (they are numbered sequentially starting with 1). If there
were any invalid ballots, print an additional line specifying the number of
such. Finally, print a line indicating the winner of the election, if any, or
indication of a tie; be certain to identify the candidates who are tied.
Separate the output for each election by a single blank line.
Sample Input
3 12
1 2 4
1 3 2
3 2 1
3 2 1
1 2 3
2 3 1
3 2 1
3 1 1
3 2 1
1 2 3
1 3 2
2 3 1
3 12
1 2 4
1 3 2
3 2 1
3 2 1
1 2 3
2 3 1
3 2 1
3 1 1
3 2 1
1 2 3
1 3 2
2 1 3
4 15
4 3 1 2
4 1 2 3
3 1 4 2
1 3 2 4
4 1 2 3
3 4 2 1
2 4 3 1
3 2 1 4
3 1 4 2
1 4 2 3
3 4 1 2
3 2 1 4
4 1 3 2
3 2 1 4
4 2 1 4
0 0
Sample Output
Election #1
2
bad ballot(s)
Candidate 3 is elected.
Election #2
2
bad ballot(s)
The following candidates are tied: 1 3
Election #3
1
bad ballot(s)
Candidate 3 is elected.
8. Easier Done than Said? (Rating:
medium-easy)
Input file: say.in Output file: say.out
Password security is a tricky thing. Users
prefer simple passwords that are easy to remember (like buddy), but such
passwords are often insecure. Some sites use random computer-generated
passwords (like xvtpzyo), but users have a hard time remembering them and
sometimes leave them written on notes stuck to their computer. One potential
solution is to generate "pronounceable" passwords that are relatively
secure but still easy to remember.
FnordCom is developing such a password
generator. You work in the quality control department, and it's your job to
test the generator and make sure that the passwords are acceptable. To be
acceptable, a password must satisfy these three rules:
1. It must contain at least one vowel.
2. It cannot contain three consecutive
vowels or three consecutive consonants.
3. It cannot contain two consecutive
occurrences of the same letter, except for 'ee' or 'oo'.
(For
the purposes of this problem, the vowels are 'a', 'e', 'i', 'o', and 'u'; all
other letters are consonants.) Note that these rules are not perfect; there are
many common/pronounceable words that are not acceptable.
Input
The input consists of one or more potential
passwords, one per line, followed by a line containing only the word 'end' that
signals the end of the file. Each password is at least one and at most twenty
letters long and consists only of lowercase letters.
Output
Foreach password, output whether or not it
is acceptable, using the precise format shown
in the example.
Example input:
a
tv
ptoui
bontres
zoggax
wiinq
eep
houctuh
end
Sample Output
<a> is acceptable.
<tv> is not acceptable.
<ptoui> is not acceptable.
<bontres> is not acceptable.
<zoggax> is not acceptable.
<wiinq> is not acceptable.
<eep> is acceptable.
<houctuh> is acceptable.
posted on 2010-09-06 00:56
CrazyNerd 阅读(2482)
评论(1) 编辑 收藏 引用 所属分类:
数据结构与算法