问题描述: 给定n种物品和一背包,物品i的重量是wi,其价值为vi,背包的容量为C。问应如何选择装入背包的物品(物品不能分割),使得装入背包中物品的总价值最大? 抽象描述如下: x[n]:表示物品的选择,x[i]=1表示选择放进物品i到背包中。 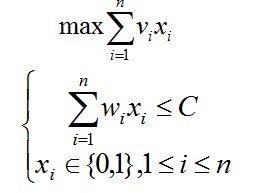 问题分析: 1.抽象之后背包问题转换为找到一个最优的数组,x1,x2,.....,xn的0-1序列。
问题分析: 1.抽象之后背包问题转换为找到一个最优的数组,x1,x2,.....,xn的0-1序列。
2.假设最优解的序列为x1,x2,.....,xn,能使背包容量C的总价值最大. 如果,x1=1,则x2,...,xn是C-w1容量的背包的总价值依然是最大的序列; 如果,x1=0,则x2,....,xn是C容量的背包的总价值依然是最大的序列。 这就是我们所说的最优子结构性质。
3.进一步分析:我们用m(i,j)表示为已经判断好了i:n的序列的背包最大价值,并且此时的背包剩余的容量为j,对物品i进行判断 如果j>wi, 就只要做出选择wi和不选择wi情况下,哪种更能使背包的总价值更大:m(i,j)=max{ m(i+1,j),m(i+1,j-wi)+vi}(注意这是个递归式) 如果j<wi: m(i,j)=m(i+1,j) 初始化: m(n,j)=vn (j>= wn); m(n,j)=0 (0<=j< wn) m(0,C)=0 最终的结果:m(1,C) 4.依次我们就得到了一个递归的表达式: 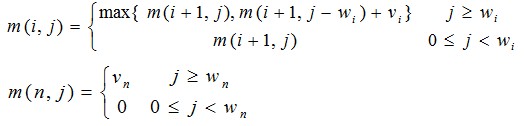
5.如果单纯的从利用递归,重复计算了很多的值,耗费的时间是很大的,动态规划还需避免这种重复计算,怎样自顶向下或自底向上的计算呢? 采用列表的方法就可以很好的分析设计自顶向下或自底向上的计算的算法了 举例分析: n=3,c=6,w={4,3,2} v={5,2,1} m[i][j]=max{ m[i+1][j], m[i+1][j-w[i]]+v[i] } 列表如下: 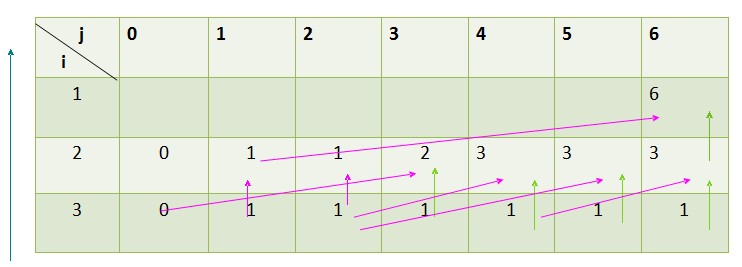 最左边箭头:我们计算的方向,从第3行开始向上计算法值。 表中红色箭头是我们通过选择做出的结果:列如 m[2][3]=max{m[3][3],m[3][3-w[2]]+v[2]},我们最终选择了m[3][3-w[2]]+v[2]。 整个问题的最优解保存在m[1][6]中。 代码实现:
最左边箭头:我们计算的方向,从第3行开始向上计算法值。 表中红色箭头是我们通过选择做出的结果:列如 m[2][3]=max{m[3][3],m[3][3-w[2]]+v[2]},我们最终选择了m[3][3-w[2]]+v[2]。 整个问题的最优解保存在m[1][6]中。 代码实现:
//w[]:保存物品重量
//v[]:保存物品价值
//n:物品数目 c:背包容量
//#define max(a,b) (((a) > (b)) ? (a) : (b))
int KnapsackDP(int n,int c)
{
int i,j;
//初始化
for (j=0;j<=c;j++)
{
if (j>=w[n])
m[n][j]=v[n];
else
m[n][j]=0;
}
for (i=n-1;i>=0;i--)
{
for (j=0;j<=c;j++)
{
if (j>=w[i])
m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
else
m[i][j]=m[i+1][j];
}
}
return m[1][c];
}
//构造选择序列x[],x[i]=1表示选择i号物品放到背包中,则x[i]=0表示不选择
void Creatx(int x[])
{
for (i=1;i<n;i++)
{
if (m[i][c]==m[i+1][c])
{
x[i]=0;
}
else
{
x[i]=1;
c-=w[i];
}
}
x[n]=m[n][c]?1:0;//m[n][C]==0则表示为没有选择第n号物品
}
实战: HDOJ 2602 http://acm.hdu.edu.cn/showproblem.php?pid=2602 
