Posted on 2008-12-25 11:21
Herbert 阅读(1501)
评论(1) 编辑 收藏 引用

假设 p2( x, y, z) 是该点,线的某坐标位置是 p1( x0, y0, z0), 线的向量是 v(xv, yv, zv)。求垂直交点 p3(xd, yd, zd)。如下图所示:
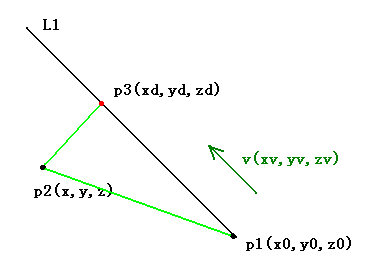
解:设有一个n,使得:
x0 + n * xv = xd; 式1
y0 + n * yv = yd; 式2
z0 + n * zv = zd; 式3
如下图所示:
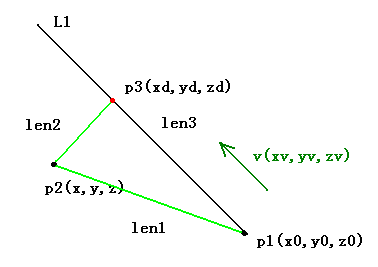
设 p2、p3的距离为 len2, p1、p2的距离为len1, p3、p1的距离为 len3。则有
len2 2 + len3 2 = len1 2 式4
又:
len1 2 = ( x – x0 ) 2 + ( y – y0) 2 + ( z – z0) 2 式5
len2 2 = ( xd – x ) 2 + ( yd – y) 2 + ( zd – z) 2 式6
len3 2 = ( xd – x 0) 2 + ( yd – y0) 2 + ( zd – z0) 2 式7
由 式1 ~式7 求得 n 。
把n 分别带入 式1 、式2 、 式3即可求得 p3 ( xd, yd, zd)。
代码实现如下: