引言
想搞正则表达式解析器好久了。前面由于一些基础设施没准备好,没法开始动手。现在 xlLib 里头准备的差不多了,可以着手实施了。
在做这件事之前,读了好几遍 @vczh 的文章《构造可配置词法分析器》《构造正则表达式引擎》(http://www.cppblog.com/vczh/archive/2008/05/22/50763.html),给了很大的帮助和启发,在这里表示感谢。(虽然到现在为止还没有完全读懂。)
编译原理理论上的东西我了解的还不是很多。正则表达式在文本解析中有着特殊的作用,特殊之一是,它的每个词法单元都是单个字符(转义的除外),因此词法分析阶段需要做的工作仅仅是转义、识别单个字符。
本文我们实现以下功能:
l 词法分析
l 语法分析
n 操作符“|”的支持
n 小括号“()”的支持(仅用于改变优先级)
词法分析
我们定义一个 Token 结构来描述一个词法单元:
| enum TokenType { TT_Eof, TT_VerticalBar, // | TT_OpenParen, // ( TT_CloseParen, // ) TT_OrdinaryChar }; struct Token { TokenType type; Char ch; size_t length; Token(TokenType type = TT_OrdinaryChar, Char ch = 0, size_t length = 1) : ch(ch), type(type), length(length) { } }; |
其中 TokenType 表示哪种类型,除了普通字符外,我们支持的单词类型有竖线、左小括号、右小括号,EOF 严格的说并不属于单词,但这里我们需要一种表示单词读尽的方法。ch 表示这个 Token 的字符,length 表示这个 Token 的字符个数,一般来说是 1,如果碰到转义的,那就不是 1。之所以要记录长度,是因为有时候试探性地多读了一个 Token 后,需要回退回去。
整个词法分析就由下面这一个函数去做:
| Token LookAhead() { if (m_nCurrentPosition >= m_strRegExp.Length()) { return Token(TT_Eof, 0, 0); } Char ch = m_strRegExp[m_nCurrentPosition++]; TokenType type = TT_OrdinaryChar; if (ch == L'\\') { if (m_nCurrentPosition < m_strRegExp.Length()) { return Token(TT_OrdinaryChar, m_strRegExp[m_nCurrentPosition++], 2); } }
switch (ch) { case L'|': type = TT_VerticalBar; break; case L'(': type = TT_OpenParen; break; case L')': type = TT_CloseParen; break; default: break; } return Token(type, ch); } |
其中 m_strRegExp 是要解析的表达式,m_nCurrentPosition 是当前位置。
我们的转义定义是,从前往后读,反斜杠 \ 后面的一个字符,转义为该字符本身。反斜杠后面跟任何字符,都是合法的。如果反斜杠出现在最后一个位置,那么容错处理,视为反斜杠这个字符。其余未经转义的,除了我们已定义功能的“|”“(”“)”外,都作为普通字符处理。目前这样的转义处理,不支持 \d、\uXXXX 之类的写法,这些以后再考虑。
顺便再写一个回退用的函数:
| void Backward(const Token &token) { m_nCurrentPosition -= token.length; } |
语法分析
文法介绍
按照本文开头定义的,我们的“正则表达式”的语法可以用以下的 EBNF 文法描述:
Expr -> ExprNoOr { "|" ExprNoOr }
ExprNoOr -> ExprNoGroup { "(" Expr ")" ExprNoGroup }
ExprNoGroup -> { OrdinaryChar }
(大概这个意思,不知道写得规不规范)
“|”的优先级最低,整个表达式(Expr)首先被第一级竖线分割成各个版本不带竖线的子式(ExprNoOr)。
每个 ExprNoOr,被括号分分隔,括号外面的是不带括号(当然也不带竖线)的子式(ExprNoGroup),括号的里面,视为一个完整的表达式(Expr)。整个 ExprNoOr,由若干个 ExprNoGroup 或者带括号的表达式连接构成。注意这里有个递归定义。到目前为止,所有的子式将终结于 ExprNoGroup。
ExprNoGroup 定义为由若干个普通字符(不含“|”“(”“)”)组成的字符串。
状态机
这个,完整的叫做“非确定有限状态机”(NFA),理论上的东西我目前不是很精确地了解,以后总结。现在把代码实现中所需要的预备知识和算法讲一下。
举个例子,对于符合我们前面定义的正则表达式“abc”,我们可以用一下的 NFA 表示:

匹配字符串的时候,我们从起始状态 S 开始,依次用每个字符区尝试匹配每一条边,如果最后走到结束状态 E,说明匹配成功。
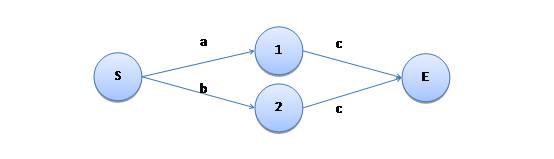
再例如“(a|b)c”,它的 NFA 表示如下:
又例如“a|ab”,它的 NFA 表示如下:
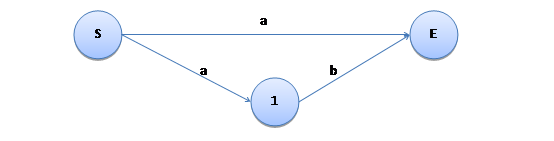
这时,一个状态后面可能有不止一条边满足某个字符的通过条件,匹配的时候可能需要进行回溯操作。
另外,由于一下代码实现实现上的原因,“a|bc”可能被弄成下面这个样子:
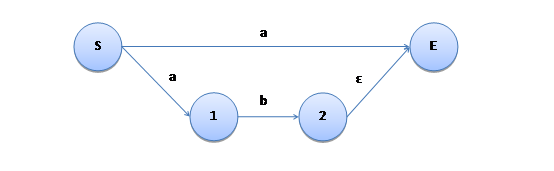
跟刚才的相比,多了一条“ε边”。ε边是一条可以不消耗字符直接通过的边。具有ε边的 NFA 叫做 ε-NFA。
好了,上面介绍了我们在本文定义的正则表达式语法中可能涉及到的状态机的样子。操作符“|”会导致状态机产生支路;括号改变优先级,体现在支路的位置不同。
我们使用一个图结构(xl::Graph)表示状态机,图的简单实现见:
http://xllib.codeplex.com/SourceControl/changeset/view/16803#160588
节点的数据结构定义如下:
| struct Node { public: Node() : m_nIdentify(++ms_nCounter) { } int m_nIdentify; static int ms_nCounter; }; __declspec(selectany) int Node::ms_nCounter = 0; |
没有特别的数据,只带一个类实例计数,以区分不同的实例。
边的数据结构定义如下:
| struct Edge { Edge() : m_bEpsilon(true), m_chBegin(0), m_chEnd(0) { } Edge(Char ch) : m_bEpsilon(false), m_chBegin(ch), m_chEnd(ch) { } Edge(Char chBegin, Char chEnd) : m_bEpsilon(false), m_chBegin(chBegin), m_chEnd(chEnd) { } bool Match(Char ch) { if (m_bEpsilon) { return false; } return (ch >= m_chBegin && ch <= m_chEnd); } bool bEpsilon; Char chBegin; Char chEnd; }; |
代码实现
我们将用一个类 xl::RegExp 来实现这个简单的“正则表达式”。一些成员变量定义如下:
| typedef Graph<Node, Edge> StateMachine; typedef SharedPtr<StateMachine> StateMachinePtr; StateMachinePtr m_spStateMachine; StateMachine::NodePtr m_pBegin; StateMachine::NodePtr m_pEnd; String m_strRegExp; int m_nCurrentPosition; |
m_spStateMachine 就是状态机,m_pBegin 和 m_pEnd 是头指针和尾指针。m_strRegExp 保存待解析的表达式,m_nCurrentPosition 是 LookAhead 里面保存当前位置的。
入口函数:
| bool Parse(const String &s) { m_strRegExp = s; m_nCurrentPosition = 0; m_spStateMachine = new StateMachine; m_pBegin = m_spStateMachine->AddNode(NewNode()); m_pEnd = Parse(m_pBegin); if (m_pEnd == nullptr) { return false; } return true; } |
简单做下初始化和准备工作,将控制权交给另一个 Parse 函数,最后检查结果。
有几个为了书写方便而引入的状态机操作函数这里先提一下:
| // 创建一个节点(不加入状态机) StateMachine::NodePtr NewNode() { return new StateMachine::NodeType(); } // 创建一条ε边(不加入状态机) StateMachine::EdgePtr NewEdge() { return new StateMachine::EdgeType(); } // 创建一条可通过一个字符的边(不加入状态机) StateMachine::EdgePtr NewEdge(Char ch) { return new StateMachine::EdgeType(Edge(ch)); } // 创建一条可通过一个区间的字符的边(不加入状态机) StateMachine::EdgePtr NewEdge(Char chBegin, Char chEnd) { return new StateMachine::EdgeType(Edge(chBegin, chEnd)); } // 从一个指定节点连一条可通过一个字符的边到新节点,返回新节点 StateMachine::NodePtr AddNormalNode(StateMachine::NodePtr pNodeFrom, Char chEdgeChar) { StateMachine::EdgePtr pEdge = NewEdge(chEdgeChar); StateMachine::NodePtr pNode = NewNode(); m_spStateMachine->AddNode(pNode); m_spStateMachine->AddEdge(pEdge, pNodeFrom, pNode); return pNode; } |
下面是依据 EBNF 而构造的一组语法分析函数,每个函数大体长成这样:
| StateMachine::NodePtr ParseXXX(StateMachine::NodePtr pNode); |
传入的是当前节点,返回的是解析完毕后的当前节点。如果出现错误,那么返回 nullptr。
重新回顾一下 EBNF:
Expr -> ExprNoOr { "|" ExprNoOr }
ExprNoOr -> ExprNoGroup { "(" Expr ")" ExprNoGroup }
ExprNoGroup -> { OrdinaryChar }
函数如下:
| StateMachine::NodePtr Parse(StateMachine::NodePtr pNode) { StateMachine::NodePtr pCurrent = ParseExpr(pNode); Token token = LookAhead(); if (token.type != TT_Eof) { return nullptr; } return pCurrent; } |
这个 Parse 并不属于 EBNF 的一部分,它也是入口性质的,为了调用 ParseExpr。因为 ParseExpr 需要处理的可能是整个表达式,也可能是括号里的子式,所以 ParseExpr 不能以 TT_Eof 作为结束,而是以不认识的字符作为结束。上面的 Parse 是针对整个表达式的,它来检验表达式是否全部解析完毕。
下面是 ParseExpr:
| StateMachine::NodePtr ParseExpr(StateMachine::NodePtr pNode) { StateMachine::NodePtr pCurrent = ParseExprNoOr(pNode); if (pCurrent == nullptr) { return nullptr; } while (true) { Token token = LookAhead(); if (token.type != TT_VerticalBar) { Backward(token); return pCurrent; } StateMachine::NodePtr pNewNode = ParseExprNoOr(pNode); StateMachine::EdgePtr pEdge = NewEdge(); m_spStateMachine->AddEdge(pEdge, pNewNode, pCurrent); } return nullptr; } |
按照文法中描述的,它首先做一遍 ParseExprNoOr,然后检查下一个字符是不是“|”,如果是,继续 ParseExprNoOr,如此循环往复。直到某一次 ParseExprNoOr 之后读到的不是“|”。
注意到此处有个并联处理。在“|”之前已经有了一个由第一次 ParseExprNoOr 产生的新节点 pCurrent,第二次(以及第三次、第四次……) ParseExprNoOr 产生的新节点 pNewNode,都用一条ε边连接到 pCurrent。
接下来是 ParseExprNoOr:
| StateMachine::NodePtr ParseExprNoOr(StateMachine::NodePtr pNode) { StateMachine::NodePtr pCurrent = pNode; while (true) { pCurrent = ParseExprNoGroup(pCurrent); if (pCurrent == nullptr) { return nullptr; } Token token = LookAhead(); if (token.type != TT_OpenParen) { Backward(token); return pCurrent; } pCurrent = ParseExpr(pCurrent); if (pCurrent == nullptr) { return nullptr; } token = LookAhead(); if (token.type != TT_CloseParen) { return nullptr; } } return nullptr; } |
它跟文法中写的形式上稍稍有点不一样。文法中是“ExprNoGroup { "(" Expr ")" ExprNoGroup }”,而现在好像是“{ ExprNoGroup "(" Expr ")" }”。其实是一样的,循环的退出点是某一次 ParseExprNoGroup 之后读到的不是“(”,要不要重复取决于“(”有没有出现。
以下是 ParseExprNoGroup,也是本文的解析终点:
| StateMachine::NodePtr ParseExprNoGroup(StateMachine::NodePtr pNode) { StateMachine::NodePtr pCurrent = pNode; while (true) { Token token = LookAhead(); if (token.type != TT_OrdinaryChar) { Backward(token); return pCurrent; } pCurrent = AddNormalNode(pCurrent, token.ch); if (pCurrent == nullptr) { return nullptr; } } return nullptr; } |
它只认普通字符,有的话把它加入状态机。
至此,我们的语法分析已经做完了,最终得到一个ε-NFA。之后我们使用这个ε-NFA来匹配字符串。
匹配检验
相对于语法分析,匹配就比较简单了。我们现在要做的工作是:已知一个正则表达式对应的ε-NFA,给出一个字符串,判定该字符串是否符合正则表达式的描述。
由于我们现在直接使用ε-NFA,所以可能需要回溯,因此,简单起见写成如下递归形式:
| bool Match(const String &s) { return Match(s, 0, m_pBegin); } bool Match(const String &s, int i, StateMachine::NodePtr pNode) { if (pNode == m_pEnd) { if (i < s.Length()) { return false; } return true; } for (auto it = pNode->arrNext.Begin(); it != pNode->arrNext.End(); ++it) { if (Match(s, i, *it)) { return true; } } return false; } bool Match(const String &s, int i, StateMachine::EdgePtr pEdge) { if (!pEdge->tValue.bEpsilon) { if (i >= s.Length()) { return false; } if (!pEdge->tValue.Match(s[i])) { return false; } return Match(s, i + 1, pEdge->pNext); } else { return Match(s, i, pEdge->pNext); } } |
第一个 Match 是入口。第二个 Match 是针对某个节点,它遍历该节点的所有后续的边,如果从某一条边解析后续字符串成功,就结束,否则继续尝试下一条边。第三个 Match 是针对某条边的,如果能通过这条边,就继续到下个节点。这里有个对ε边的特殊处理,如果是ε边,i 没有加一,直接到下个节点。
上述过程是一个深度优先的搜索过程,如果能走到最后的节点,且字符串也刚刚走到最后,算匹配成功。
单元测试
先做一些常规的测试:
| XL_TEST_CASE() { RegExp r; XL_TEST_ASSERT(r.Parse(L"")); XL_TEST_ASSERT(r.Parse(L"||")); XL_TEST_ASSERT(r.Parse(L"()")); XL_TEST_ASSERT(r.Parse(L"|")); XL_TEST_ASSERT(r.Parse(L"(|)")); XL_TEST_ASSERT(r.Parse(L"(||)")); XL_TEST_ASSERT(r.Parse(L"()|()")); XL_TEST_ASSERT(!r.Parse(L"(")); XL_TEST_ASSERT(!r.Parse(L")")); } XL_TEST_CASE() { RegExp r; XL_TEST_ASSERT(r.Parse(L"")); XL_TEST_ASSERT(r.Match(L"")); XL_TEST_ASSERT(!r.Match(L"a")); XL_TEST_ASSERT(r.Parse(L"a")); XL_TEST_ASSERT(r.Match(L"a")); XL_TEST_ASSERT(!r.Match(L"ab")); XL_TEST_ASSERT(!r.Match(L"b")); XL_TEST_ASSERT(r.Parse(L"(a)")); XL_TEST_ASSERT(r.Match(L"a")); XL_TEST_ASSERT(!r.Match(L"ab")); XL_TEST_ASSERT(!r.Match(L"b")); XL_TEST_ASSERT(r.Parse(L"ab|c")); XL_TEST_ASSERT(!r.Match(L"a")); XL_TEST_ASSERT(!r.Match(L"b")); XL_TEST_ASSERT(r.Match(L"c")); XL_TEST_ASSERT(r.Match(L"ab")); XL_TEST_ASSERT(!r.Match(L"bc")); XL_TEST_ASSERT(!r.Match(L"ac")); XL_TEST_ASSERT(r.Parse(L"a(b|c)")); XL_TEST_ASSERT(!r.Match(L"a")); XL_TEST_ASSERT(!r.Match(L"b")); XL_TEST_ASSERT(!r.Match(L"c")); XL_TEST_ASSERT(r.Match(L"ab")); XL_TEST_ASSERT(r.Match(L"ac")); XL_TEST_ASSERT(!r.Match(L"bc")); } XL_TEST_CASE() { RegExp r; XL_TEST_ASSERT(r.Parse(L"\\|")); XL_TEST_ASSERT(r.Match(L"|")); XL_TEST_ASSERT(r.Parse(L"\\(")); XL_TEST_ASSERT(r.Match(L"(")); XL_TEST_ASSERT(r.Parse(L"\\)")); XL_TEST_ASSERT(r.Match(L")")); XL_TEST_ASSERT(r.Parse(L"\\\\")); XL_TEST_ASSERT(r.Match(L"\\")); XL_TEST_ASSERT(r.Parse(L"\\")); XL_TEST_ASSERT(r.Match(L"\\")); XL_TEST_ASSERT(r.Parse(L"\\|(\\(|\\))")); XL_TEST_ASSERT(r.Match(L"|(")); XL_TEST_ASSERT(r.Match(L"|)")); } |
嗯……没有成就感。再来点有意思的。我们目前虽然只支持“|”和“(”“)”,但能做的事情已经很多了,比如匹配 0 到 255 的数字。
我们将 0 到 255 的数分为五类:
1. 一位数:(0|1|2|3|4|5|6|7|8|9)
2. 两位数:(0|1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)
3. 三位数:
a) 0到199:(0|1)(0|1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)
b) 200到249:2(0|1|2|3|4)(0|1|2|3|4|5|6|7|8|9)
c) 250到255:25(0|1|2|3|4|5)
将这五个使用“|”连起来,就是一个0到255的正则表达式。
| XL_TEST_CASE() { RegExp r; XL_TEST_ASSERT(r.Parse(L"(0|1|2|3|4|5|6|7|8|9)|" L"(0|1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)|" L"(0|1)(0|1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9)|" L"2(0|1|2|3|4)(0|1|2|3|4|5|6|7|8|9)|" L"25(0|1|2|3|4|5)")); XL_TEST_ASSERT(r.Match(L"0")); XL_TEST_ASSERT(r.Match(L"1")); XL_TEST_ASSERT(r.Match(L"2")); XL_TEST_ASSERT(r.Match(L"3")); XL_TEST_ASSERT(r.Match(L"4")); XL_TEST_ASSERT(r.Match(L"5")); XL_TEST_ASSERT(r.Match(L"6")); XL_TEST_ASSERT(r.Match(L"7")); XL_TEST_ASSERT(r.Match(L"8")); XL_TEST_ASSERT(r.Match(L"9")); XL_TEST_ASSERT(r.Match(L"10")); XL_TEST_ASSERT(r.Match(L"20")); XL_TEST_ASSERT(r.Match(L"30")); XL_TEST_ASSERT(r.Match(L"40")); XL_TEST_ASSERT(r.Match(L"50")); XL_TEST_ASSERT(r.Match(L"60")); XL_TEST_ASSERT(r.Match(L"70")); XL_TEST_ASSERT(r.Match(L"80")); XL_TEST_ASSERT(r.Match(L"90")); XL_TEST_ASSERT(r.Match(L"100")); XL_TEST_ASSERT(r.Match(L"199")); XL_TEST_ASSERT(r.Match(L"200")); XL_TEST_ASSERT(r.Match(L"249")); XL_TEST_ASSERT(r.Match(L"250")); XL_TEST_ASSERT(r.Match(L"251")); XL_TEST_ASSERT(r.Match(L"252")); XL_TEST_ASSERT(r.Match(L"253")); XL_TEST_ASSERT(r.Match(L"254")); XL_TEST_ASSERT(r.Match(L"255")); XL_TEST_ASSERT(!r.Match(L"256")); XL_TEST_ASSERT(!r.Match(L"260")); XL_TEST_ASSERT(!r.Match(L"300")); } |
我们可以 YY 下现在的状态机的样子: