今天08、09的个人排位赛，出了下面这道，一开始看觉得很难，后来推出来了后就不是很难了。
   哈哈，只有我一个人做出来，下面说下怎么做。
 题目定义一种叫做n-circle five-angle 的图，问生成树的个数，每个点都算一个不同的点

 

Illustration 1: 4-circle five-angle graph

   首先，中间的环肯定要去掉一些，但是去掉多少条、哪几条呢？
   可以枚举情况。就拿样例说，我们去掉任意的两条，得到下图：

   红色的边表示去掉的。
   1）对于非红色边组成的环，4条边任意一条都能删除，即4n-i 这里i是中间环要删除的边数
   2）对于红色边组成的环，这4*i条边只能删除一条，删多了就会不连通了，也即4*i种
   再乘上一个组合数C(n,i)即可
   所以F(n) = ∑ 4n-i*4*i*C(n,i)    1≤i≤n
   样例给了2，注意是2条平行边形成的环！
   
#include<cstdio>
#include<cstring>

int C[101][101],F[101];

int pow4(int n)//4^n
{
    int ans=1,p=4;
    while(n)
    {
        if(n&1)ans=ans*p%2007;
        p=p*p%2007;
        n>>=1;
    }
    return ans;
}
int main()
{
    //freopen("in","r",stdin);
    //freopen("out","w",stdout);
    for(int i=1;i<=100;i++)
    {
        C[i][i]=C[i][0]=1;
        for(int j=1;j<i;j++)
            C[i][j]=(C[i-1][j]+C[i-1][j-1])%2007;
    }
    for(int n=2;n<=100;n++)
    {
        F[n]=0;
        for(int i=1;i<=n;i++)
            F[n]=(F[n]+pow4(n-i)*4*i*C[n][i])%2007;
    }
    int n,T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        printf("%d\n",F[n]);
    }        
    return 0;
}



附题目：

 

Problem A. Spanning Tree

A peculiar graph, called n-circle five-angle graph, consists of a polygon with n vertices in the center, and each side of the central polygon is linked with a pentagon(pentagon: a polygon with 5 sides). There is an example of 4-circle five-angle graph below. Obviously, there are 4 vertices in the central polygon.

Now, it is you time to calculate how many spanning trees could this special graph generate. Pay attention that all the vertices in the graph should be regarded as different ones. Do you still remember the definition of spanning tree? Perhaps you may be familiar with the terminology of MST(minimal spanning tree). Yes, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some (or perhaps all) of the edges of G.



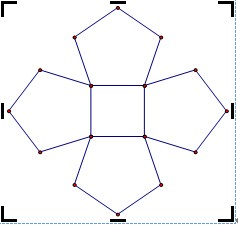
Illustration 1: 4-circle five-angle graph

Input:

First line: T, the number of test case.

Then follow T lines, each line contains a number n(n <= 2 <= 100), indicating it is an n-circle five-angle graph.

 

Output：

For each test case, output the answer mod 2007 pre line.

 

Sample Input

1

2

 

Sample Output

40

 
测试数据：in.txt   out.txt