   /**//* /**//*
 题意:给出N,x,M 要计算 题意:给出N,x,M 要计算
 N N
 ∑(k^x)*(x^k) MOD M ∑(k^x)*(x^k) MOD M
 k=1 k=1
 x x
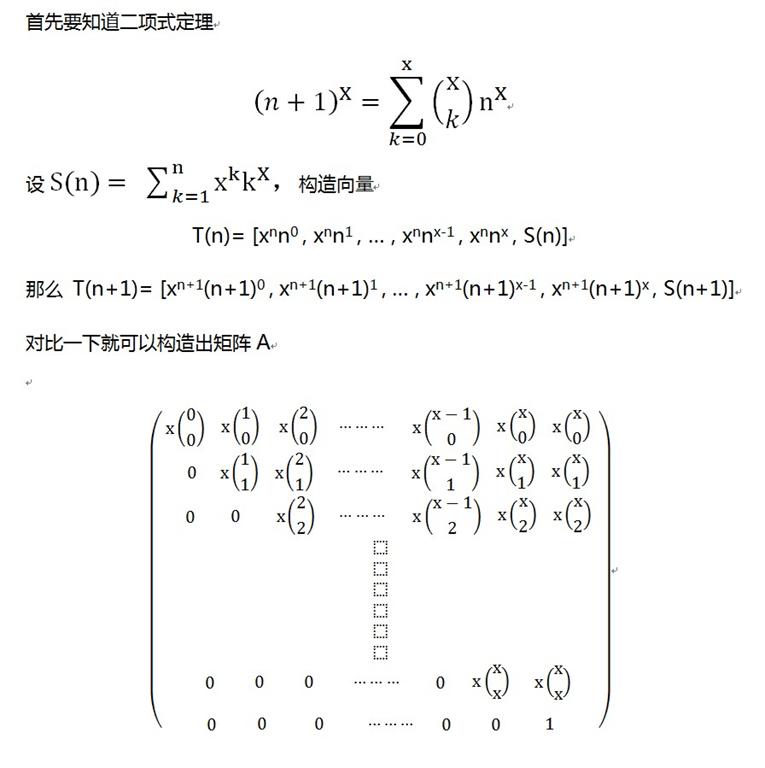
 用到二项式定理,(n+1)^x = ∑C(x,k)n^k 用到二项式定理,(n+1)^x = ∑C(x,k)n^k
 k=0 k=0
 然后构造矩阵,求和 S(n)表示前n项和 然后构造矩阵,求和 S(n)表示前n项和
 */ */
 #include<cstdio> #include<cstdio>
 #include<cstring> #include<cstring>

 long long C[55][55],A[55][55],start[55]; long long C[55][55],A[55][55],start[55];
 int M,N,x; int M,N,x;

 void init() void init()
   { {
 for(int i=0;i<=x;i++)C[i][0]=C[i][i]=1; for(int i=0;i<=x;i++)C[i][0]=C[i][i]=1;
 for(int i=2;i<=x;i++) for(int i=2;i<=x;i++)
 for(int j=1;j<i;j++) for(int j=1;j<i;j++)
   { {
 C[i][j]=C[i-1][j]+C[i-1][j-1]; C[i][j]=C[i-1][j]+C[i-1][j-1];
 if(C[i][j]>=M)C[i][j]%=M; if(C[i][j]>=M)C[i][j]%=M;
 } }
 //init A [0 //init A [0 x+1][0 x+1][0 x+1] x+1]
 memset(A,0,sizeof(A)); memset(A,0,sizeof(A));
 for(int j=0;j<=x;j++) for(int j=0;j<=x;j++)
 for(int i=0;i<=j;i++) for(int i=0;i<=j;i++)
   { {
 A[i][j]=x*C[j][i]; A[i][j]=x*C[j][i];
 if(A[i][j]>=M)A[i][j]%=M; if(A[i][j]>=M)A[i][j]%=M;
 } }
 for(int i=0;i<=x;i++) for(int i=0;i<=x;i++)
   { {
 A[i][x+1]=x*C[x][i]%M; A[i][x+1]=x*C[x][i]%M;
 if(A[i][x+1]>=M)A[i][x+1]%=M; if(A[i][x+1]>=M)A[i][x+1]%=M;
 } }
 A[x+1][x+1]=1; A[x+1][x+1]=1;
 for(int j=0;j<=x+1;j++)start[j]=x;//N=1时 for(int j=0;j<=x+1;j++)start[j]=x;//N=1时
 } }
 void mul(long long A[][55],long long B[][55])//A=A*B void mul(long long A[][55],long long B[][55])//A=A*B
   { {
  long long R[55][55]= long long R[55][55]= {0}; {0};
 for(int k=0;k<=x+1;k++) for(int k=0;k<=x+1;k++)
 for(int i=0;i<=x+1;i++) for(int i=0;i<=x+1;i++)
 if(A[i][k]) if(A[i][k])
 for(int j=0;j<=x+1;j++) for(int j=0;j<=x+1;j++)
   { {
 R[i][j]+=A[i][k]*B[k][j]; R[i][j]+=A[i][k]*B[k][j];
 if(R[i][j]>=M)R[i][j]%=M; if(R[i][j]>=M)R[i][j]%=M;
 } }
 for(int i=0;i<=x+1;i++) for(int i=0;i<=x+1;i++)
 for(int j=0;j<=x+1;j++) for(int j=0;j<=x+1;j++)
 A[i][j]=R[i][j]; A[i][j]=R[i][j];
 } }
 void pow(long long m[][55],int n)//m=A^n void pow(long long m[][55],int n)//m=A^n
   { {
 if(n==1) if(n==1)
   { {
 for(int i=0;i<=x+1;i++) for(int i=0;i<=x+1;i++)
 for(int j=0;j<=x+1;j++) for(int j=0;j<=x+1;j++)
 m[i][j]=A[i][j]; m[i][j]=A[i][j];
 return ; return ;
 } }
 pow(m,n/2); pow(m,n/2);
 mul(m,m); mul(m,m);
 if(n&1)mul(m,A); if(n&1)mul(m,A);
 } }
 int main() int main()
   { {
 //freopen("in","r",stdin); //freopen("in","r",stdin);
 while(scanf("%d%d%d",&N,&x,&M),N>0) while(scanf("%d%d%d",&N,&x,&M),N>0)
   { {
  if(N==1) if(N==1) {printf("%d\n",x%M);continue;} {printf("%d\n",x%M);continue;}
 init(); init();
 long long ans[55][55]; long long ans[55][55];
 pow(ans,N-1); pow(ans,N-1);
 long long res=0; long long res=0;
 for(int i=0;i<=x+1;i++) for(int i=0;i<=x+1;i++)
 res+=start[i]*ans[i][x+1]; res+=start[i]*ans[i][x+1];
 printf("%I64d\n",res%M); printf("%I64d\n",res%M);
 } }
 return 0; return 0;
 } }

|
|
常用链接
随笔分类
Links
搜索
最新评论

|
|