题意:自己看吧。
分析:终于通过这道题弄懂了树状数组。
首先这里我不具体解释 int Lowbit() { i + (- i ) } 来源,我只想
强调的是数组C【i】保存的是C[i - 2^k +1] 到C[i] 区间的状态,k 值是 i 二进制表示中末尾0的个数。
我的理解就是树状数组有两种操作down ,up,都是对区间状态的操作,或者点状态的操作,注意一点的就是只是状态(包括简单的和,个数的
统计,本题翻转次数的统计)的查询与修改。树状数组的结构就是多叉树形结构,up(即 i + Lowbit(i))是逐级向上处理父区间(注意我说的是父区间),
down (即:i - Lowbit(i))要注意的是 down 不是逐级向下找子区间并进行操作,而是找左边相邻的兄弟区间(我不知道这样描述准不准确,
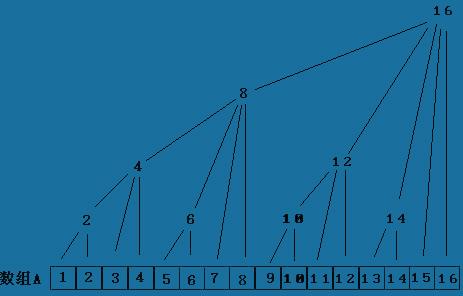
你可以看那张经典的树状数组的结构图再自己算算就很明了了)。正因为这样,树状数组能方便的查询父区间(UP操作),而不能方便的访问子区间,
只能方便访问左边相邻的兄弟区间(down操作),我觉得这就是它相对于线段树的不足之处,不过还是很强大的了。
所以,当遇到具体的问题时,只要记住只是区间状态(和,个数,翻转次数。。。。)的访问,具体的操作是用down还是up就很好理解了。
对于本题,change时是对区间段的翻转次数进行修改所以是down(依次向左对兄弟区间进行修改),当Query时,其实就是统计点覆盖点(x,y)各区间的总翻转次数所以是向上(up)查询父区间的过程,你可以自己模拟一下就很明了。
实现的CPP代码如下:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 1005
int mat[N][N];
int n;
int lowbit(int key){
return key&(-key);
}
int getsum(int x, int y){
int ans = 0;
for(int i=x; i<=n; i+=lowbit(i))
for(int j=y; j<=n; j+=lowbit(j))
ans = (ans+mat[i][j])%2;
return ans;
}
void change(int x, int y){
for(int i=x; i>0; i-=lowbit(i))
for(int j=y; j>0; j-=lowbit(j))
mat[i][j] = (mat[i][j]+1)%2;
}
int main(){
int t;
char si[10];
scanf("%d",&t);
while(t--){
int m;
scanf("%d%d",&n,&m);
memset(mat,0,sizeof(mat));
for(int i=0; i<m; i++){
scanf("%s",si);
if(si[0]=='C'){
int x1,y1,x2,y2;
scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
change(x2,y2);
change(x1-1,y2);
change(x2,y1-1);
change(x1-1,y1-1);
}else{
int x1,y1;
scanf("%d%d",&x1,&y1);
printf("%d\n",getsum(x1,y1));
}
}
printf("\n");
}
return 0;
}