今天浙大月赛dp+数学专场。。俩小盆友不在,哥这个从来不写dp和数学的人表示很蛋疼。
很少写dp,很少写概率。哪怕写了一道水题也很高兴哇~
写一下吧~
题目大意:
说你手里有n个生物,n-1个人,1个吸血鬼。每一天,你从这堆里面随机挑出两头来,如果是不同种,那么人就有p的概率会被同化为吸血鬼。
求一个期望,问给定n和p的情况下,所有人变吸血鬼的期望天数D。
做法:
首先是要看出最基本的式子,就是在n个生物,n-x个人,x个吸血鬼的情况下抽出两头不同生物的概率:
假设分先后抽,那么先抽吸血鬼x / n , 后抽人 (n - x) / (n - 1) , 概率为 x * ( n - x) / (n * (n - 1));先抽人 (n - x) / n , 后抽吸血鬼 x / (n - 1) , 概率为 x * (n - x) / (n * ( n - 1))。
所以th[x](表示在n个生物,n-x个人,x个吸血鬼的情况下抽出两头不同生物的概率) = 2 * x * (n - x) / (n * (n - 1))。
然后就可以得出在某轮已有x个吸血鬼的前提下,吸血鬼数量增加1的概率为f[x] = th[x] * p 。而不变的概率则为g[x] = 1.0 - f[x]。
则可以建立如下概率转移图。Sx表示当前有x个吸血鬼。第k层的Sx的表示,到了第k-1天,有x个吸血鬼(的概率转移)。
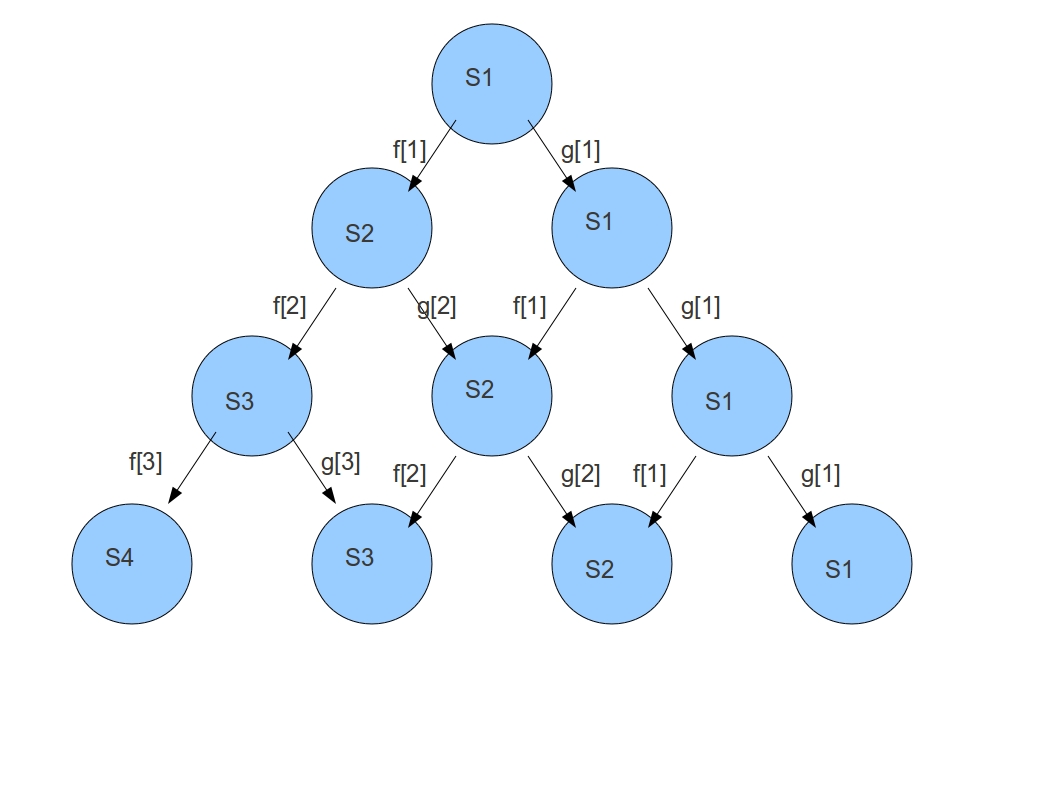
所以可以看出Sx只和Sx-1和Sx本身有关。假设DP[x]表示由初始状态变成有x个吸血鬼所需天数的期望。
DP[x] = sigma(i = 1 to infinity)[f[x-1] * i * g[x-1] ^ (i - 1)]
而最终的期望即为所有期望之和ans = sigma(i=2 to n) DP[i]。
题目的关键就是DP[x]的求解,仔细观察这是一个等差乘等比的无穷级数求和,根据高中所学的错位相减法得到公式:
设Sn=DP[x],a=f[x-1],p=g[x-1]。则Sn-p*Sn=a+a*p+a*p^2....+a*p^n-1-n*a*p^n
Sn=[a*(1-p^n) - n*(1-p)*p^n]/(1-p)^2
lim(n->inf)Sn=a/(1-p)^2=1/a
所以最后的ans=sigma(1/a[i])=sigma(1.0/(2.0*p*i*(n-i)/(n*(n-1))))。
因为n在10^5级别,所以要用double乘,不然int会爆精度。
我也是可以做数学题的哈。
å
forward sentence