随笔档案

   对于开放列表的维护方案来说，前面我说的，都是一些小花样了，在一些很小的地图上用他们并没有什么太大的问题，但是如果地图很大，需要搜寻的格子很多，那么开放列表里的元素必然会很多，那么我们是否可以用另外一种思维来考虑一下开放列表的维护工作？
 
   其实我们每次从开放列表里面取值，每次只需要取里面所有元素的最小值就行了，而前面所说的两种方案都有自己的优点，第一种不需要对开放列表做排序，但每次找起最小值来实在消耗很大，第2种在找最小值的时候只需取第一个元素就行，而麻烦在于需要一直维持开放列表里面所有元素的有序排列，那么我们是不是可以把这两种方法的优点都结合起来呢

   当然，这种方法是有的，那就是很多高级A*程序更苛求速度的一种做法，利用Binary Heap数据结构，也就是二叉堆，来维护开放列表。

   其实有关二叉堆，相信了解他的高手很多，我就不再班门弄斧，，其实我也只是刚刚学习他而已，这里只简单的介绍一下他的一些特点以及在A*中他所起到的作用。

   百度百科中对二叉堆的定义： 二叉堆是一种特殊的堆，二叉堆是完全二元树或者是近似完全二元树。二叉堆满足堆特性：父结点的键值总是大于或等于任何一个子节点的键值。

   那么应用于A*的开放列表里，我们只要反过来，父结点的键值总是小于或等于任何一个子节点的键值，这样就没问题了。

   利用这种特性进行过排列的开放列表，那么我们可以保证，具有F值特性最小的那个元素，肯定是在这个二插树的根节点，于是取值的时候，只要把根节点上的值取出来用就行了。（当然，取完以后还得维护开放列表的二叉堆特性，这点我下面会谈），一般来说，二叉堆是利用数组来表示，那么正好，我所使用的vector结构便可以派上用场，二插堆的结构填往vector中的时候，利用的是一种类似前序遍历的方式顺序进入的，也就是按照 当前节点 -- 当前节点的左子节点 -- 当前节点的右子节点这样的顺序来放入vector中，如下图


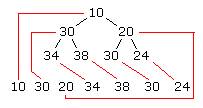
（此图是借用了Panic所翻译的《在A*寻路中使用二叉堆》一文中的图片）

不过根节点进入的时候不要放在0号元素上，vector可以随便先放进一个没有用的元素，我处理的时候是放了一个NULL型指针进去的，也就是说根节点所在的vector下标为1。而这样的话对于这个vector中非0下标的任意一个元素，我们要找他的父节或者是子节点就很简单了，遵循下面一个原则：
具备二叉堆特性的vector中下标为n(n!=0)的一个元素：
他的父节点下标 = n / 2;(小数去掉)    比如下标为9的元素，他的父节点下标就是4
他的左子节点下标 = n * 2;  右子节点下标 = n * 2 +1   比如下标为3的元素他的左子节点下标为6,右子节点下标为7

   对于我们的A*来说，在把元素放进开放列表里面的时候就需要按照二叉堆的添加步骤进行操作，而我们在把下标1的F值最小的元素取出来并且删除掉以后，则需要把二叉堆重新维护下其二叉堆的特性，而在寻路过程中某个开放列表中元素的G值改变以后，我们则需要对这个开放列表再进行次维护，维持他的二叉堆特性。那么综合以上，我们只需要3个功能函数，BinaryHeapAdd函数，BinaryHeapDelete函数，RetaxisBinaryHeap函数

BinaryHeapAdd函数，
1 把新的要进入开放列表的元素放进vector的末尾，也就是直接push_back进去 （这个新加进的元素为当前处理元素）
2 利用上面所说的父子节点下标关系，找到当前处理元素的父节点下标，然后比较两个数，如果新的元素比他的父节点小，则把这个元素和他的父节点的位置互换一下，如果产生了互换行为，则针对新位置上的这个当前处理元素再次重复本次动作；
3 直到新的元素大于等于他的父节点，或者找到的父节点下标为0 ，则新元素的位置确定为找到，这个函数可以结束

void AStarBase::BinaryHeapAdd(POINTINFO* indexPoint)
{
    int tmpF = indexPoint->F;

    _openPoint.push_back(indexPoint);        //先把新的元素放在vector最后

    int theNewIndex = _openPoint.size()-1;   //新元素的下标
    while (true)
    {
        int theParentIndex = theNewIndex / 2;     //新元素当前所在位置的父节下标
        if (theParentIndex != 0)                  
        {
            if (_openPoint[theNewIndex]->F < _openPoint[theParentIndex]->F)   //新元素的F值比他的父节点值大
            {
                //与父节点的位置进行交换
                POINTINFO* tmpinfo = _openPoint[theParentIndex];
                _openPoint[theParentIndex] = _openPoint[theNewIndex];
                _openPoint[theNewIndex] = tmpinfo;

                _openPoint[theParentIndex]->openIndex = theParentIndex;
                _openPoint[theNewIndex]->openIndex = theNewIndex;

                theNewIndex = theParentIndex;   //置新节点的处理下标为换过位置以后的值
            }
            else
            {
                break;
            }
        }
        else                                    //如果父节下标计算出来为0，则停止查找位置
        {
            break;
        }
    }
}

BinaryHeapDelete函数
1 把开放列表中1号元素取出并放在最后返回出来使用

2 需要对开放列表进行一次2叉堆特性重新维护，首先把vector中最后一个元素移动到1号下标位置，（1号元素为当前处理元素）

3 对1号下标位置的当前处理元素利用父子节点下标计算关系找出他的左子节点和右子节点，然后把这个元素与他的左子节点元素的F值和右子节点的F值大小分别做比较，如果子节点的比他更小，则把他与子节点的位置进行互换，如果两个子节点的值都比他小，则与较小的那个子节点进行位置互换，如果产生了互换行为，则针对新位置上的当前处理元素再次进行本次动作

4 如果子节点的值都大于或者等于当前处理元素的值，或者计算出来的子节点下标已经朝出了vector最大元素个数，则停止排序，函数可以返回原来存起来的最小值

AStarBase::POINTINFO* AStarBase::BinaryHeapDelete()
{
     if (_openPoint.size() <= 1)   //开放列表里面只剩下开始放进去的一个空的POINTINFO指针
     {
          return NULL;
     }

     //先把最后一个元素放到1号位置
     POINTINFO* tmpinfo = _openPoint[1];    //下标1位置的元素先存储起来，函数结束的时候要return出去
     _openPoint[1] = _openPoint.back();    //把vector中的最后一个元素放到下标1位置
     _openPoint.pop_back();
     _openPoint[1]->openIndex = 1;

     int theSelectIndex = 1;       //要处理元素的下标值
     while (true)
     {
         int theLeftChildIndex = theSelectIndex * 2;               //左子节点下标值
         int theRightChildIndex    = theSelectIndex * 2 + 1;          //右子节点下标值
         if (theLeftChildIndex >= _openPoint.size())   //这个数没有子节点，则停止排序
         {
             break;                                   
         }
         else if ( theLeftChildIndex == (_openPoint.size() -1)) //左子节点正好是vector中最后一个元素，即只有左子节点，没有右子节点
         {
             if (_openPoint[theSelectIndex]->F > _openPoint[theLeftChildIndex]->F)   //如果父节点的F值比左子节点更大
             {
                 //交换
                 POINTINFO* tmptmpinfo = _openPoint[theLeftChildIndex];
                 _openPoint[theLeftChildIndex] = _openPoint[theSelectIndex];
                 _openPoint[theSelectIndex] = tmptmpinfo;

                 _openPoint[theLeftChildIndex]->openIndex = theLeftChildIndex;
                 _openPoint[theSelectIndex]->openIndex = theSelectIndex;

                 theSelectIndex = theLeftChildIndex;
             }
             else  //如果小，则停止排序
             {
                 break;
             }
         }
         else if (theRightChildIndex < _openPoint.size())  //既有左子节点又有右子节点
         {
             if (_openPoint[theLeftChildIndex]->F <= _openPoint[theRightChildIndex]->F )   //左右子节点先互相比较 左边的小
             {
                 if (_openPoint[theSelectIndex]->F > _openPoint[theLeftChildIndex]->F)      //处理的父节点F值比左子节点大
                 {
                     //交换(与左子节点)
                     POINTINFO* tmptmpinfo = _openPoint[theLeftChildIndex];
                     _openPoint[theLeftChildIndex] = _openPoint[theSelectIndex];
                     _openPoint[theSelectIndex] = tmptmpinfo;     

                     _openPoint[theLeftChildIndex]->openIndex = theLeftChildIndex;
                     _openPoint[theSelectIndex]->openIndex = theSelectIndex;
              
                     theSelectIndex = theLeftChildIndex;
                 }
                 else
                 {
                     break;
                 }
             }
             else     //右边的比较小
             {
                 if (_openPoint[theSelectIndex]->F > _openPoint[theRightChildIndex]->F)      //处理的F值比右子节点大
                 {
                     //交换(与右子节点)
                     POINTINFO* tmptmpinfo = _openPoint[theRightChildIndex];
                     _openPoint[theRightChildIndex] = _openPoint[theSelectIndex];
                     _openPoint[theSelectIndex] = tmptmpinfo;

                     _openPoint[theRightChildIndex]->openIndex = theRightChildIndex;
                     _openPoint[theSelectIndex]->openIndex = theSelectIndex;
   
                     theSelectIndex = theRightChildIndex;
                 }
                 else
                 {
                     break;
                 }    
             }
         }

     }
     return tmpinfo;
}

大家可以看到，上面的两个函数所做的添加和删除操作，可以保证开放列表里，1号位置的元素的F值肯定是最小的，而其他地方的大小位置关系，我们可以不需要理会，我们只要保持一个原则，2叉堆里的父节点元素F值不能比子节点大，就可以了

而寻路过程中由于F值重计算而导致的重排序，其实和添加操作的原理是一样的，我们只需要把那个改过F值的元素，把他和他的父节点的F值进行比较，如果改过的值小，则互换，如果并不小或者没有了父节点，则停止
void AStarBase::RetaxisBinaryHeap(int index)
{
    int theNewIndex = index;   //当前处理的下标
    while (true)
    {
        int theParentIndex = theNewIndex / 2;     //当前处理节点的父节点下标值
        if (theParentIndex != 0)
        {
            if (_openPoint[theNewIndex]->F < _openPoint[theParentIndex]->F)   //新进来的F值比他的父节点值大
            {
                //进行交换
                POINTINFO* tmpinfo = _openPoint[theParentIndex];
                _openPoint[theParentIndex] = _openPoint[theNewIndex];
                _openPoint[theNewIndex] = tmpinfo;

                _openPoint[theParentIndex]->openIndex = theParentIndex;
                _openPoint[theNewIndex]->openIndex = theNewIndex;

                theNewIndex = theParentIndex;
            }
            else
            {
                break;
            }
        }
        else
        {
            break;
        }
    }
}

利用上面3个操作函数所算出来的寻路结果，与一开始使用在无序开放列表里每次利用比较法找出最小F值所得到的结果是一样的，
POINT(2,2)寻路到 POINT(398,398)



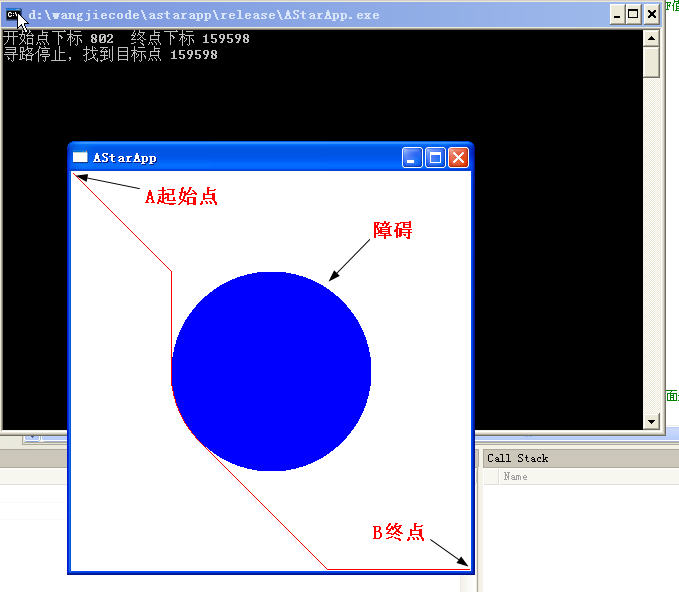
好吧，其实我们用他的目的是什么？就是要看看他消耗的速度而已，让我们来看一下性能分析表


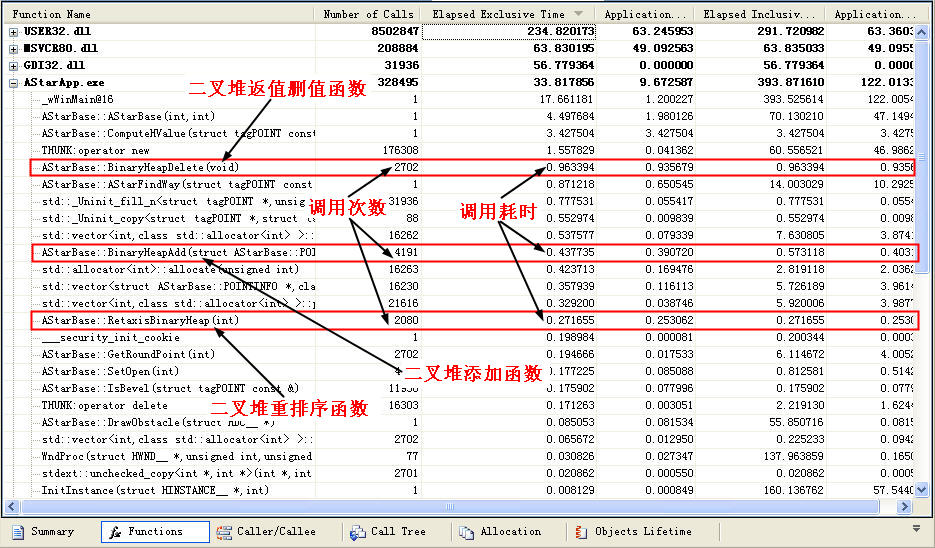
大家可以看到，在整个程序中这3个函数所消耗的时间为 0.963394 + 0.437735 + 0.271655 = 1.672784毫秒，是无序找最小值方法所使用时间的十分之一左右，是使用正常一些全排序方法消耗速度的六分之一左右，这还是在路径非常简单的情况下，而一旦障碍更多，路径更复杂，开放列表里的元素更多的时候，Binary Heap方法能体现他更大的速度优势

以上代码没有经过任何优化工作，仅仅是实现了下二叉堆的功能，各位将就着看了 ^O^

如果对A*寻路基础算法原理不清楚并且有兴趣的朋友，可以去gameres上看一下这篇文章
http://data.gameres.com/message.asp?TopicID=25439