|
|
OpenGL发展的历史:
OpenGL的前身是SGI公司所开发的IRIS GL图形函数库,OpenGL不是一种编程语言,而是一个更像C运行时函数库。OpenGL是一个开放的工业标准,虽然它是由SGI首创,但它的标准不是控制在SGI手中,而是由OpenGL体系结构审核委员会(ARB)掌管。ARB是由SGC、DEC、IBM、Intel和Microsoft等著名公司于1992年创立,后来陆续加了nVidia、ATI等图形芯片领域的巨擎。ARB每4年开一次会,对OpenGL规范进行维护和改善,并出台计划对OpenGL标准进行升级,使OpenGL一直与时代保持同步。
2006年,SGI公司把OpenGL标准的控制从ARB移交给Khronos小组(www.khronos.org)。Khronos是一个由成员提供资金的行业协会,专注于开放媒体标准的创建和维护。目前Khronos负责OpenGL的发展和升级。
如图:
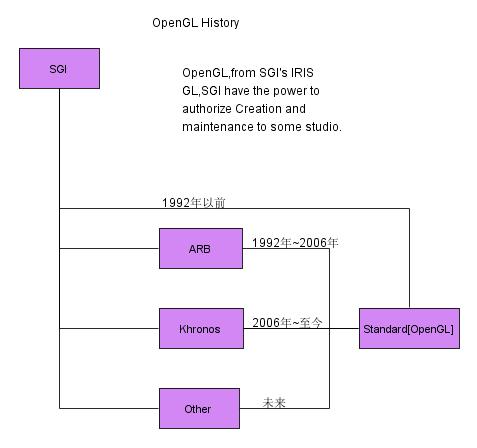
与OpenGL相关的函数库:
OpenGL工具函数库(GLU)包含了一些函数,它们利用低层的OpenGL函数来执行一些特定的任务。设定特定的矩阵(gluLookAt等),OpenGL中的GLU必须以glu开头。
对于窗口系统的功能也进行了扩展,如果在linux下使用x窗口的话,使用GLX函数库,而必须以glX开头。对于微软来说,以wgl开头。IBM的os/2而言,PGL是显示管理器与OpenGL之间的接口,以pgl开头。对于Apple,AGL是支持OpenGL的系统接口,所有的AGL函数都以agl开头。
OpenGL实用工具库( GLUT,OpenGL Utility Toolkit )是Mark Kilgrad所编写的一个独立于窗口系统的工具包,它的目的是隐藏不同窗口系统所带来的复杂性。GLUT是下一节的主题,GLUT函数以glut开头。
在OpenGL中,我们常用到轨迹球,下面就对轨迹球来做点东西:
当我们观察三维空间的物体有很多种方法让一个用户来选择一个视点,但是我认为轨迹球是最好的。
轨迹球的基本原理是:
创建一个围绕着物体的球,然后用户单击球上面的一个点,再拖动这个点到一个位置(在屏幕上),让对象跟着这个向量旋转。
寻找鼠标位置:
第一步就是寻找到鼠标的位置,我们可以通过获得视见变换矩阵。
可以通过下面的形式来获得状态矩阵:
  GLdouble projection_matrix[16] = GLdouble projection_matrix[16] =  { 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 }; { 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 };
  GLdouble modelview_matrix[16] = GLdouble modelview_matrix[16] =  { 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 }; { 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1 };
  int viewport_matrix[4] = int viewport_matrix[4] =  { 0, 0, 640, 480 }; { 0, 0, 640, 480 };

 glGetDoublev( GL_PROJECTION_MATRIX, projection_matrix ); glGetDoublev( GL_PROJECTION_MATRIX, projection_matrix );
 glGetDoublev( GL_MODELVIEW, modelview_matrix ); glGetDoublev( GL_MODELVIEW, modelview_matrix );
 glGetIntegerv( GL_VIEWPORT, viewport_matrix ); glGetIntegerv( GL_VIEWPORT, viewport_matrix );我们获取这些矩阵后面使用,我们可以使用他们来处理鼠标输入,鼠标坐标mouse_x和mouse_y,可以通过gluUnProject来获得鼠标下面场景中的一个点。
 GLdouble x, y, z; GLdouble x, y, z;
 gluUnProject( mouse_x, mouse_y, gluUnProject( mouse_x, mouse_y,
 modelview_matrix, modelview_matrix,
 projection_matrix, projection_matrix,
 viewport_matrix, viewport_matrix,
 &x, &y, &z ); &x, &y, &z );一旦场景中的这个点被找到,问题的关键就是建立一个从摄象机位置到这个点的光线,然后寻找这个光线和这个轨迹球的交点。这个光线是E + t * ( P - E )的点集,这里E是眼睛点位置,P是场景中的那个点,t是一个变量,而轨迹球是S的点集,这里S^2 = r,r是轨迹球的半径。如果S = E + t * ( P - E ),那么存在一个点既在轨迹球上,又在光线上,这样,我们可以通过带入法推出:( E + t * ( P - E ) ) ^ 2 = r。我们知道向量E、P以及标量r,所以可以推出来t,这是一个二次方程,如果无解,说明光线和轨迹球无交点。如果有2个解,应当选择最靠近眼睛的那个解。
轨迹球的旋转问题:
如果你单击拖拽轨迹球上的一个点到另一个位置,该如何做呢?
一个简单的方法,做起点到结束点的x乘为旋转轴,然后寻找将要旋转的角度,这个可以通过做点乘得到。
计算旋转矩阵:
我们通过四元数来解决它。四元数是二维复数的扩展,特别适合做旋转。
如果我们有一个单位向量( x, y, z ),我们可以通过乘以旋转角度的正弦的一半获得四元数的x, y, z部分的修正值,w是由旋转角的的余弦的一半决定。大家知道所有的这么值可以被组装进一个旋转矩阵:
 w * w + x *x - y * y - z * z, 2 * x * y + 2 * w * z, 2 * x * z - 2 * w * y, 0 w * w + x *x - y * y - z * z, 2 * x * y + 2 * w * z, 2 * x * z - 2 * w * y, 0
 2 * x * y - 2 * w * z, w * w - x * x + y * y - z * z, 2 * y * z + 2 * w * x, 0 2 * x * y - 2 * w * z, w * w - x * x + y * y - z * z, 2 * y * z + 2 * w * x, 0
 2 * x * z + 2 * w * y, 2 * y * z - 2 * w * x, w * w - x * x - y * y + z * z, 0 2 * x * z + 2 * w * y, 2 * y * z - 2 * w * x, w * w - x * x - y * y + z * z, 0
 0, 0, 0, w * w + x * x + y * y + z * z 0, 0, 0, w * w + x * x + y * y + z * z

|