Triangle Conjecture
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Special Judge
Problem Description
One could construct a triangle with the digit 1 to 9 as the figure below:
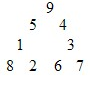
The
triangle is the one that the sums of every four numbers on its three
edges are all equals to 23. Moreover, 23 is the biggest summation one
can get from this kind of arraignment of digits. Your task is even
tougher, given a positive integer n, you should use integer from 1 to
3*(n-1) to construct triangle with equal summation of digits on the
three edges and the summation is the biggest among all the possible
arraignments. For example, if n = 4, then you should choose number from 1
to 3*(4-1).
For convenience, the output format for a certain triangle is like the example for the figured triangle above:
95 41 38 2 6 7
The numbers are separated by a single space in each row, and there are no spaces at the end of each row.
Note that there may be several solutions exist, arbitrary one of them will be accepted.
Input
The first line of the input contains a number t indicates the number of test cases.
Following
t lines, each line will contains only one integer n denoting the side
length of the desired triangle. ( t≤20, 3≤n≤1000)
Output
For each test case, output the triangles one by one.
Sample Input
Sample Output
Author
ahui
Source
ACM-DIY Group Contest 2011 Spring
找规律,n 分奇偶处理,比赛时仓促,代码不很简洁
1 #include <stdio.h>
2
3 #define N 1009
4
5 int a[ N ], b[ N ], c[ N ], m, n;
6
7 void solveOdd() {
8 int i = 1;
9 m = 0;
10 while ( i <= 3*n-6 ) {
11 if ( i&1 ) {
12 a[ m ] = i++;
13 b[ m ] = i++;
14 c[ m ] = i++;
15 }
16 else {
17 c[ m ] = i++;
18 b[ m ] = i++;
19 a[ m ] = i++;
20 }
21 ++m;
22 }
23 }
24
25 void solveEven() {
26 int i;
27 for ( i = 1; i <= n-2; ++i ) {
28 b[ i-1 ] = n-2+i;
29 }
30 a[ 0 ] = 2;
31 a[ 1 ] = 3*n-6;
32 c[ 0 ] = 1;
33 c[ 1 ] = 3*n-7;
34 m = 2;
35 i = 2;
36 while ( m < n-2 ) {
37 ++i;
38 a[ m ] = i;
39 a[ m+1 ] = 3*n-5-i;
40 ++i;
41 c[ m ] = i;
42 c[ m+1 ] = 3*n-5-i;
43 m += 2;
44 }
45 }
46
47 void swap( int a[], int b[], int *sa, int *sb ) {
48 int i, tmp;
49 tmp = *sa;
50 *sa = *sb;
51 *sb = tmp;
52 for ( i = 0; i < m; ++i ) {
53 tmp = a[ i ];
54 a[ i ] = b[ i ];
55 b[ i ] = tmp;
56 }
57 }
58
59 void solve() {
60 int sa, sb, sc, i;
61 if ( n & 1 ) {
62 solveOdd();
63 }
64 else {
65 solveEven();
66 }
67 sa = sb = sc = 0;
68 for ( i = 0; i < m; ++i ) {
69 sa += a[ i ];
70 sb += b[ i ];
71 sc += c[ i ];
72 }
73 if ( sa < sb ) {
74 swap( a, b, &sa, &sb );
75 }
76 if ( sa < sc ) {
77 swap( a, c, &sa, &sc );
78 }
79 if ( sb < sc ) {
80 swap( b, c, &sb, &sc );
81 }
82 }
83
84 void output() {
85 int i;
86 printf( "%d\n", 3*n-3 );
87 for ( i = 0; i < m; ++i ) {
88 printf( "%d %d\n", c[ i ], b[ i ] );
89 }
90 printf( "%d", 3*n-4 );
91 for ( i = 0; i < m; ++i ) {
92 printf( " %d", a[ i ] );
93 }
94 printf( " %d\n", 3*n-5 );
95 }
96
97 int main() {
98 int td;
99 scanf( "%d", &td );
100 while ( td-- > 0 ) {
101 scanf( "%d", &n );
102 solve();
103 output();
104 }
105 return 0;
106 }
107