一、用向量空间解方程组
1、向量和向量空间
(1) 二维空间R2中的向量用两个沿列向的元素表示。

向量u,v在二维空间的表示:
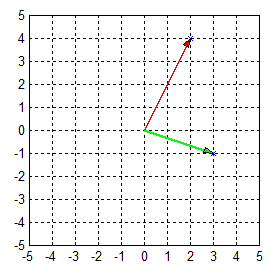
(2) 二维向量张成的空间
平面上的任何一点[w1;w2]是不是一定能用u和v的线性组合来实现?即是不是一定能找到一组常数[c1,c2],使得

• c1,c2取所有可能的值,得到的w的集合就是u和v张成的子空间,在所给的u和v下,它是一个平面。
• 若u和v两个向量的各元素成简单的比例关系,合成的向量只能在一根直线上,不可能张成整个二维平面。这种情况下,称这两个向量u和v是线性相关的。
(3) 三维空间中的向量
若v1,v2和v3都是三维空间的列向量。可以用空间坐标中的三个点,或从坐标原点引向这三点的箭头来表示。用矩阵代数表示如下:
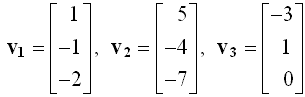
如果三个基本向量之间线性无关,那么它们的线性组合可以覆盖(张成)整个三维空间。如果三个向量共面,即相关,就不能张成三维空间。判断三个向量的线性相关性,可用行列式。
(4) 三维空间向量的相关性
det(A)=0 相关
det(A)≠0 不相关
行列式的几何意义:在二维是两个向量组成的平行四边形面积,在三维是三个向量组成的平行六面体的体积。
(5) n维向量的相关性
在进入三维以上的空间时,已经没有可与面积、体积直接相当的概念可用了,所以采用了秩的概念。如果A的行列式为零,也就是它的秩r小于n时,说明这n个向量是线性相关的。
秩的概念也概括了面积存在(r=2)和体积存在(r=3)的意义,因此,它是更高度的抽象。
(6) 向量空间和基向量
• 若r个向量是线性无关的,则它们的线性组合的全体V就构成了r维空间Rr。如果它不是空集,则V称为向量空间。生成V的r个线性无关的向量v称为基向量或基(Basis)。
• 当r=n时,给定的n个向量就是一组基。如果r<n,那就要在n个向量中选出r个线性无关的向量。用秩的概念还无法判定哪些向量是线性无关的,这时又要藉助于把矩阵简化为阶梯形式的方法。
例1:求四个五维向量的子空间
这四个向量组成的矩阵如下,对它进行行阶梯简化:
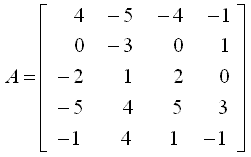
程序为:
>> A=[4,-5,-4,-1;0,-3,0,1;-2,1,2,0;-5,4,5,3;-1,4,1,-1]
[U0,ip]=rref(A)
A =
4 -5 -4 -1
0 -3 0 1
-2 1 2 0
-5 4 5 3
-1 4 1 -1
U0 =
1 0 -1 0
0 1 0 0
0 0 0 1
0 0 0 0
0 0 0 0
ip =
1 2 4
>>
得到 ip=1,2,4,其三个枢轴列对应的就是三个线性无关的列向量。
例2:w是否在v1,v2,v3的空间内
设
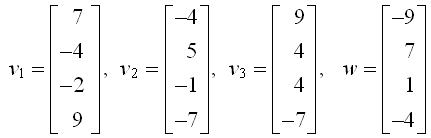
w是否能由v1,v2,v3的线性组合构成的问题,取决于线性方程组 v.c=w 解的存在性。
程序为:
v1=[7;-4;-2;9];
v2=[-4;5;-1;-7];
v3=[9;4;4;-7];
w=[-9;7;1;-4];
v=[v1,v2,v3];
c=v\w
% 把基向量组成矩阵v求解
也可以按det(v)是否为零进行判别。
(7) 向量的内积和正交性
两个m维向量的内积可以写成:
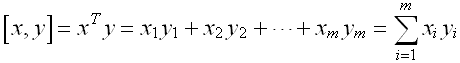
这是一个标量。向量x与自己求内积
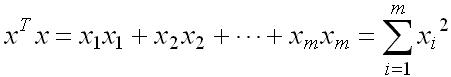
得到的是其各分量的平方和,其平方根就等于向量的长度(或模、或范数norm)。
(8) 内积的几何意义
在平面情况,两向量的内积除以它们的长度是它们夹角的余弦:
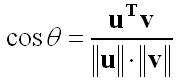
例3:基向量长度规一化和夹角
求以上例2中的单位基向量v01,v02,v03,并分别求它们之间的夹角。
程序为:
v10=v1/norm(v1)
v20=v2/norm(v2)
v30=v3/norm(v1)
theta12=acos((v1'*v2)/(norm(v1)*norm(v2)))
theta13=acos((v1'*v3)/(norm(v1)*norm(v3)))
theta23=acos((v3'*v2)/(norm(v3)*norm(v2)))
(9) 正交基向量的生成
两向量x,y正交的条件是它们的内积为零。
给出向量求正交基常用施密特算法,ATLAST手册中给出了相应的程序gschmidt。调用时键入[Q,R]=gschmidt(v),Q就是单位正交基向量e。
MATLAB中不用施密特算法,而用更好的算法编成了正交分解子程序qr.m,它将v分解为Q和R两个矩阵的乘积。调用方法为:[Q,R]=qr(v) ,Q就是m×m单位正交矩阵。
基向量正交化的schmidt公式:

得到qi(i1,2,…,k)后,再把它们除以norm(qi),就可归一化为单位向量ek。
基向量正交化的gschmidt子程序:
function [Q,R]=gschmidt(V)
[m,n]=size(V); R=zeros(n);
R(1,1)=norm(V(:,1));
Q(:,1)=V(:,1)/R(1,1);
for k=2:n
R(1:k-1,k)=Q(:,1:k-1)'*V(:,k);
Q(:,k)=V(:,k)-Q(:,1:k-1)*R(1:k-1,k);
R(k,k)=norm(Q(:,k));
Q(:,k)=Q(:,k)/R(k,k);
end
例4:对于例2的数据,求其规范化正交基向量e1,e2,…,en。
>> V=[7,-4,9;-4,5,4;-2,-1,4;9,-7,-7]
[Q,R]=qr(V) % 或 [Q,R]=gschmidt(V)
e=Q(:,[1:3])
V =
7 -4 9
-4 5 4
-2 -1 4
9 -7 -7
Q =
-0.5715 -0.3164 -0.7473 -0.1217
0.3266 -0.6096 -0.1080 0.7142
0.1633 0.7144 -0.5022 0.4591
-0.7348 0.1339 0.4216 0.5141
R =
-12.2474 8.8998 1.9596
0 -3.4341 -3.3662
0 0 -12.1173
0 0 0
e =
-0.5715 -0.3164 -0.7473
0.3266 -0.6096 -0.1080
0.1633 0.7144 -0.5022
-0.7348 0.1339 0.4216
>>
得到e=[e1 e2 e3]
二、线性变换及特征
1、平面上线性变换的几何意义
例1 设x为二维平面上第一象限中的一个单位方块,其四个顶点的数据可写成:
x =
0 1 1 0
0 0 1 1
把不同的A矩阵作用于此组数据,可以得到多种多样的结果yi=Ai*x。

可以看出,矩阵A1使原图对纵轴生成镜像,矩阵A2使原图在横轴方向膨胀,矩阵A3使原图在纵轴方向压缩,矩阵A4使原图向右方剪切变形,矩阵A5使原图沿反时针方向旋转tpi/6。分别计算出这五个矩阵的行列式和特征值: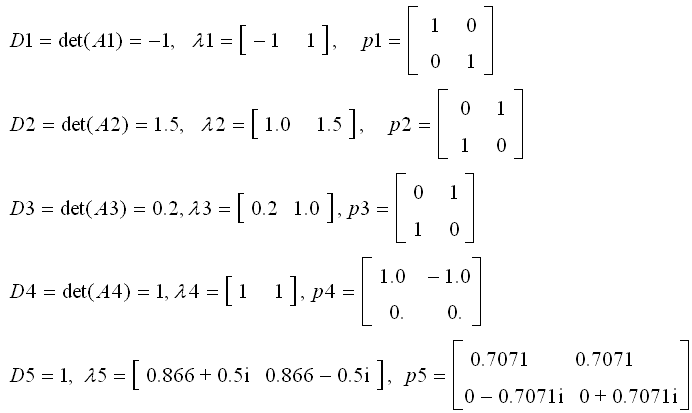
对二维空间(平面),行列式的几何意义实际上是两个向量所构成的平行四边形的面积。一个变换所造成的图形的面积变化,取决于该变换的行列式。A1,A4和A5的行列式绝对值都是1,所以它们不会使变换后图形的面积发生改变。而A2和A3的行列式分别为1.5和0.2。
2、二维矩阵特征值的几何意义
(1) 二维矩阵的特征值表示该变换在原图形的特征向量的方向上的放大量。例如矩阵A1在第一特征向量
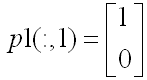
的方向的特征值为λ1(1) = -1,即横轴正方向的增益为-1,其结果是把原图中横轴正方向的部分变换到新图的负方向去了;A1在第二特征向量
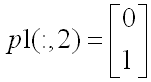
的方向的特征值为λ1(2)=1,即纵轴正方向的增益为1,因而保持了新图和原图在纵轴方向尺度不变。
例2:斜体字的生成
数据矩阵
x =
0 0.5000 0.5000 6.0000 6.0000 5.5000 5.5000 0
0 0 6.4200 0 8.0000 8.0000 1.5800 8.0000
表示英文大写空心字母N的各个节点
(1)用plot语句在子图1中画出其形状;
(2)取
A =
1 0.25
0 1
作为变换矩阵对x进行变换,并在子图2中画出其图形;
画图的要点是要在给定的数据右方,补上第一点的坐标,使画出的图形封闭。
程序为:
x0 = [0,0.5,0.5,6,6,5.5,5.5,0;0,0,6.42,0,8,8,1.58,8]
x = [x0,x0(:,1)] % 把首顶点坐标补到末顶点后
A = [1,0.25;0,1]
y = A*x
subplot(1,2,1), plot(x(1,:),x(2,:))
subplot(1,2,2), plot(y(1,:),y(2,:))
画出的两个图形为:

(2) 平移运动不能用二维变换实现
刚体在平面上的运动要用两个平移和一个转动来描述,转动可以从上面的线性变换A5得到,但平移y=x+c却不是一个线性变换。因为:
(1)设ya = xa+c;yb = xb+c;则它们的和为
y = ya+yb = xa+xb+2c ≠ x+c,
可见,它对加法不封闭;
(2)设ya = xa+c;将它乘以常数k,
y = kya = k(xa+c) = kxa+kc ≠ kxa+c = x+c,
可见,它对乘法也不封闭;就是说,这不符合线性变换的规则,x和y 不属于同一个向量空间,无法用矩阵乘法来实现平移变换y = x+c。
(3) 平面运动模型的齐次坐标系
把平面问题映射到高维的空间来建立方程,有可能把x和y由扩展了的向量空间来覆盖。把原来通过原点的平面沿垂直方向提高一个单位,与原平面保持平行,于是原来的x就用三维向量来表示为:

这样的坐标系称为齐次坐标系。
此时可以把平移矩阵写成:
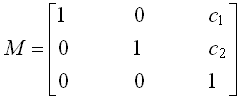
因而平移运动y就可用x经线性变换实现了。
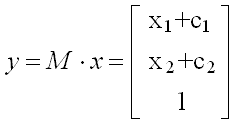
这个方法在研究刚体平面运动时非常有用。
对象若同时有旋转和平移,则可以分别列出旋转矩阵和平移矩阵。不过此时的旋转矩阵也要改为3×3维,这可以把上述A5中增加第三行和第三列,置A(3,3)=1,其余新增元素为零。
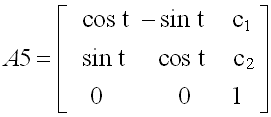
这就是既包括平移,又包括转动的平面齐次坐标系内的变换矩阵。
(4) 空间线性变换的几何意义
三维空间线性变换最直接的几何意义和应用价值可以从飞行器的三维转动坐标中得到解释。飞行器在空中可以围绕三个轴旋转。假如它在向北飞行,机头正对北方,则它围绕铅垂轴的旋转角称为偏航角(Yaw),它描述了飞机左右的偏转,用u表示;围绕翼展轴的旋转角称为倾斜角(Pitch),它描述了飞机俯仰姿态,用v表示;围绕机身轴的旋转角称为滚动角(Roll),用w表示;u,v和w三个变量统称为欧拉角,它们完全地描述了飞机的姿态。
例3:程序的实现方法
把飞行器的三维图像用N个顶点描述,写成一个3×N的数据矩阵G。用plot3命令时按顶点连线能绘制出飞行器的外观。例如以下程序即可画出一个最简单的飞行器立体图。
Gw=[-4,-3,0;4,-3,0;0,7,0;-4,-3,0]'; % 主翼的顶点坐标
Gt=[0,-3,0;0,-3,3;0,2,0;0,-3,0]'; % 尾翼的顶点坐标
G=[Gw,Gt] % 整个飞行器外形的数据集
plot3(Gw(1,:),Gw(2,:),Gw(3,:),'r'), hold on
plot3(Gt(1,:),Gt(2,:),Gt(3,:),'g'), axis equal
围绕各个轴的旋转变换矩阵:
飞行器围绕各个轴的旋转的结果,表现为各个顶点坐标发生变化,也就是G的变化。只要把三种姿态的变换矩阵Y,P和R乘以图形数据矩阵G即可。其中

综合旋转的变换矩阵:
单独变化某个姿态角所生成的图形由G1 = Y*G,G2 = P*G,G3 = R*G算出,如果同时变化三个姿态角,则最后的图像数据成为Gf = Y*P*R*G = Q*G。这里假定转动的次序为:先滚动R,再倾斜P,最后偏航Y,由于矩阵乘法不服从交换律,转动次序不同时结果也不同。
用MATLAB实现的程序如下:
>> syms u,w,v
Y=[cos(u),sin(u),0;-sin(u),cos(u),0;0,0,1]
R=[1,0,0;0,cos(w),-sin(w);0,sin(w),cos(w)]
P=[cos(v),0,-sin(v);0,1,0;sin(v),0,cos(v)]
Q=Y*P*R
w =
w
v =
v
Y =
[ cos(u), sin(u), 0]
[ -sin(u), cos(u), 0]
[ 0, 0, 1]
R =
[ 1, 0, 0]
[ 0, cos(w), -sin(w)]
[ 0, sin(w), cos(w)]
P =
[ cos(v), 0, -sin(v)]
[ 0, 1, 0]
[ sin(v), 0, cos(v)]
Q =
[ cos(u)*cos(v), sin(u)*cos(w)-cos(u)*sin(v)*sin(w), -sin(u)*sin(w)-cos(u)*sin(v)*cos(w)]
[ -sin(u)*cos(v), cos(u)*cos(w)+sin(u)*sin(v)*sin(w), -cos(u)*sin(w)+sin(u)*sin(v)*cos(w)]
[ sin(v), cos(v)*sin(w), cos(v)*cos(w)]
>>