B-Spline Curve Library in Open Cascade
Open Cascade中的B样条曲线库
eryar@163.com
摘要Abstract：简要介绍Open Cascade中的B样条曲线库BSplCLib的使用方法，并且结合源程序来对Open Cascade中的B样条曲线的组成部分如节点矢量、重复度等概念进行介绍，以及通过对计算B样条基函数的算法进行分析，加深对B样条曲线概念的理解。
关键字Key Word：B Spline Curve、Open Cascade、Knot Vector、Multiplicity
一、 概述 Overview
1946年由Schoenberg提出了B样条理论，给出了B样条的差分表达式；1972年de Boor和Cox分别独立给出了关于B样条的标准算法。Gordon和Riesenfeld又把B样条理论用于形状描述，最终提出了B样条方法。用B样条基替代了Bernstein基，构造出B样条曲线，这种方法继承了Bezier方法的一切优点，克服了Bezier方法存在的缺点，较成功地解决了局部控制问题，又轻而易举地在参数连续性基础上解决了连接问题，从而使自由曲线曲面形状的描述问题得到较好解决。
p次B样条曲线的定义为：
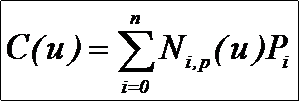
其中：
l Pi是控制顶点（control point）；
l Ni,p(u)是定义在非周期节点矢量上的p次B样条基函数；
有很多方法可以用来定义B样条基函数以及证明它的一些重要性质。例如，可以采用截尾幂函数的差商定义，开花定义，以及由de Boor和Cox等人提出的递推公式等来定义。我们这里采用的是递推定义方法，因为这种方法在计算机实现中是最有效的。
令U={u0,u1,…,um}是一个单调不减的实数序列，即ui<=ui+1，i=0,1,…,m-1。其中，ui称为节点，U称为节点矢量，用Ni,p(u)表示第i个p次B样条基函数，其定义为：
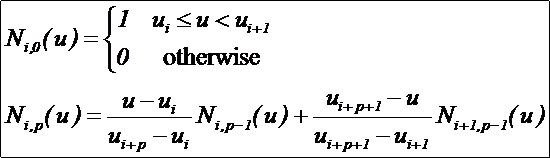
B样条基有如下性质：
a) 递推性；
b) 局部支承性；
c) 规范性；
d) 可微性；
根据B样条曲线定义可知，给定控制顶点Pi（control points），曲线次数p（degree）及节点矢量U（knot vectors），B样曲线也就确定。对于有理B样条曲线，还需要参数权重（weights）。
二、 OCC中的B样条曲线库 BSplCLib in OCC
在Open Cascade中的工具箱（Toolkit）TKMath中的包（package）BSplCLib是B样条曲线库，为B样条曲线曲面的计算提供了支持。它提供了三方面的功能：
l 对节点矢量（knot vectors）及重复度（multiplicities）的管理；
l 对多维样条的支持，即B样条方法中控制顶点的维数可以是任意维数（dimension）；
l 二维和三维样条曲线的方法；
Open Cascade中的B样条曲线由下列数据项定义：
|
定义 |
变量类型 |
变量名称 |
|
控制顶点control points |
TColgp_Array1OfPnt |
Poles |
|
权重weights |
TColStd_Array1OfReal |
Weights |
|
节点knots |
TColStd_Array1OfReal |
Knots |
|
重数multiplicities |
TColStd_Array1OfInteger |
Mults |
|
次数degree |
Standard_Integer |
Degree |
|
周期性periodicity |
Standard_Boolean |
Periodic |
B样条曲线库BSplCLib提供了一些基本几何算法：
l B样条基函数及其导数的计算BSplCLib::EvalBsplineBasis()；
l 节点插入BSplCLib::InsertKnot()；
l 节点去除BSplCLib::RemoveKnot()；
l 升阶BSplCLib::IncreaseDegree()；
l 降阶；
结合《The NURBS Book》和Open Cascade中的BSplCLib的源程序，可以高效的学习NURBS。《The NURBS Book》中有详细的理论推导及算法描述，而Open Cascade中有可以用来实际使用的程序。理论联系实际，有助于快速理解NURBS的有关概念及其应用。
三、 OCC中B样条曲线库的节点和重数Knots and Multiplicity in BSplCLib
由B样条曲线的可微性可知，节点的重数与B样条曲线的连续性相关。在节点区间内部，Ni,p(u)是无限次可微的，因在每个节点区间内部，它是一个多项式。在节点处Ni,p(u)是p-k次连续的，其中k是节点的重复度（multiplicity，有时也称为重数）。因此，增加次数p将提高曲线的连续性，而增加节点的重复度则使连续性降低。
重复度（multiplicity，有时也称为重数）有两种不同的理解方式：
l 节点在节点矢量中的重复度；
l 节点相对于一个特定的基函数的重复度；
在Open Cascade中对重复度的理解是前者，即节点在节点矢量中的重复度。下面结合源程序来进行说明。
函数BSplCLib::Knots()用来将给定的节点矢量（节点序列knot sequence）转换为节点的重复度不大于1的Knots数组和每个节点对应的重复度Mults数组，且数据Knots和Mults的长度必由函数BSplCLib::KnotsLength()得到。Knots()函数的源程序如下所示：
//=======================================================================
//function : Knots
//purpose : Computes the sequence of knots Knots without repetition
// of the knots of multiplicity greater than 1.
// Length of <Knots> and <Mults> must be KnotsLength(KnotSequence,Periodic).
//=======================================================================
void BSplCLib::Knots(const TColStd_Array1OfReal& SeqKnots,
TColStd_Array1OfReal &knots,
TColStd_Array1OfInteger &mult,
// const Standard_Boolean Periodic)
const Standard_Boolean )
{
Standard_Real val = SeqKnots(1);
Standard_Integer kk=1;
knots(kk) = val;
mult(kk) = 1;
for (Standard_Integer jj=2;jj<=SeqKnots.Length();jj++)
{
// test on strict equality on nodes
if (SeqKnots(jj)!=val)
{
val = SeqKnots(jj);
kk++;
knots(kk) = val;
mult(kk) = 1;
}
else
{
mult(kk)++;
}
}
}
从上述代码可知，直接使用了不等于来判断两个节点的值是否相同，而没有采用误差处理，即严格的相等比较。程序将节点重复度不大于1的节点及其相应的重复度分别保存到knots和mult中。
四、 B样条曲线的分类 B Spline Curve Type
B样条曲线一般按定义基函数的节点序列是否等距（均匀）分为均匀B样条曲线（Uniform B-Spline Curve）和非均匀B样条曲线（Non Uniform B-Spline Curve）。
B样条曲线按节点序列中节点分布情况不同，又分为四种类型：均匀B样条曲线、准均匀B样条曲线、分段Bezier曲线、一般非均匀B样条曲线。设给定特征多边形顶点Vi，i=0,1,…,n，曲线次数k，则有：
l 均匀B样条曲线（uniform B-Spline curve）：节点序列中节点沿参数轴均匀或等距分布，即所有节点区间长度为大于零的常数（constant）：
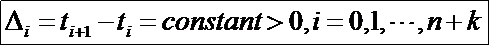
l 准均匀B样曲线（quasi-uniform B-Spline curve）：其节点序列中两端节点具有重复度k+1，而所有内节点均匀分布，具有重复度1。
l 分段Bezier曲线（piecewise Bezier curve）：其节点序列中两端节点重复度与准均匀B样条曲线的相同，所不同的是所有内节点重复度为k。
l 非均匀B样条曲线（general non-uniform B-Spline curve）：这是对任意分布的节点序列，只要在数学上成立，即节点序列非递减，都可取。
在基础类模块（Module FoundationClasses）的工具箱（Toolkit TKMath）中的包（GeomAbs）中有对B样样条曲线类型的定义，源程序如下所示：
//! This enumeration is used to note specific curve form. <br>
enum GeomAbs_BSplKnotDistribution {
GeomAbs_NonUniform,
GeomAbs_Uniform,
GeomAbs_QuasiUniform,
GeomAbs_PiecewiseBezier
};
而类BSplCLib主要是用来管理节点和重复度的，所有将节点和重复度也进行了分类。根据节点矢量是否均匀分布，将节点分配方式（Knot Distribution）分为：均匀（BSplCLib_Uniform）和非均匀（BSplCLib_NonUniform）。源程序如下所示：
enum BSplCLib_KnotDistribution {
BSplCLib_NonUniform,
BSplCLib_Uniform
};
根据重复度数组将重复度的分配方式分为如下三种类型：
n BSplCLib_Constant：重复度都相同；
n BSplCLib_QuasiConstant：首、尾节点的重复度与内部节点的重复度不同；
n BSplClib_NonConstant：其它情况；
源程序如下所示：
enum BSplCLib_MultDistribution {
BSplCLib_NonConstant,
BSplCLib_Constant,
BSplCLib_QuasiConstant
};
判断节点矢量和重复度矢量类型分别由下列函数实现：
l BSplCLib::KnotForm()；
l BSplCLib::MultForm()；
具体的判断方法可以查看源程序。
将节点分布方式与重复度的分布方式进行组合，可以得出B样条曲线的那几种类型。
五、 B样条基函数的计算 Evaluate the B-Spline Basis
B样条基函数的计算主要使用了B样条基了函数的递推公式（Cox-deBoor公式）的局部支撑性质，如下所示：
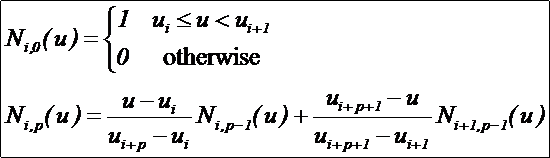
直接由定义可知：
l Ni,0(u)是一个阶梯函数，它在半开区间u∈[ui, ui+1)外都为零；
l 当次数p>0时，Ni,p(u)是两个p-1次基函数的线性组合；
l 计算一组基函数需要事先指定节点矢量U和次数p；
l 半开区间[ui,ui+1)称为第i个节点区间（knot span），它的长度可以为零，因为相邻节点可以是相同的；
l 计算p次基函数的过程可以生成一个如下形式的三角形陈列：
B样条有局部支撑性，即若u不在区间[ui, ui+p+1)，则Ni,p(u)=0。可从下面的三角形中看出N1,3是N1,0、N2,0、N3,0和N4,0的线性组合，而N1,0在区间[u1, u2)上非零，N2,0在区间[u2,u3)上非零，N3,0在区间[u3,u4)上非零，N4,0在区间[u4,u5)上非零，所以N1,3仅在区间[u1,u5)上非零。
在任意给定的节点区间[uj,uj+1)内，最多有p+1个是非零的，它们是Nj-p,p、Nj-p+1、…、Nj,p。例如，在[u3,u4)上，零次基函数中只有N3,0是非零的，一次基函数只有N2,1和N3,1是非零的，非零的三次基函数只有N0,3、N1,3、N2,3、N3,3。这个性质如下图所示：
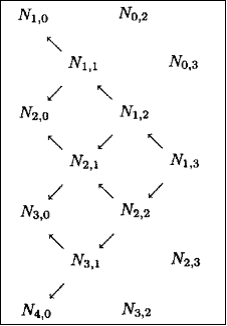
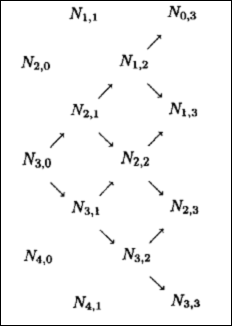
上面两幅图中右边的图中所示的推算过程表明，给定节点序列U及B样条曲线的次数p，给出任意一个u值，找出其所在的节点区间[ui,ui+1)上，最多有Ni-p,p，Ni-p+1,p，…，Ni,p个非零的基函数。
例如我们根据递推公式写出二次基函数的一般形式，如下所示：
当给定的u值在区间[u3,u4)上即（i=3）时，根据上面的三角形，得出下列重要结论：
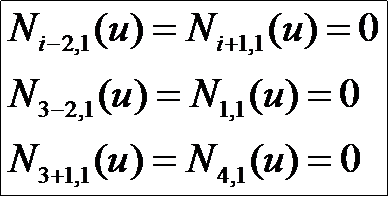
即这两项不需要计算。另外一个重要结论就是图中用相同颜色框中的部分是相同的，也就是下面程序中的变量temp表示的内容。
我们引入下面符号：
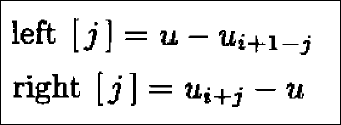
由二次基函数推出的三个公式可写为：
上述推导过程为《The NURBS Book》中的算法，算法代码如下所示：
理解了变量temp的意义之后，整个程序就很好理解了。
将Open Cascade中计算基函数的算法是不同的，将其源程序摘抄如下所示：
//=======================================================================
//function : Build BSpline Matrix
//purpose : Builds the Bspline Matrix
//=======================================================================
Standard_Integer
BSplCLib::EvalBsplineBasis
//(const Standard_Integer Side, // = 1 rigth side, -1 left side
(const Standard_Integer , // = 1 rigth side, -1 left side
const Standard_Integer DerivativeRequest,
const Standard_Integer Order,
const TColStd_Array1OfReal& FlatKnots,
const Standard_Real Parameter,
Standard_Integer& FirstNonZeroBsplineIndex,
math_Matrix& BsplineBasis)
{
// the matrix must have at least DerivativeRequest + 1
// row and Order columns
// the result are stored in the following way in
// the Bspline matrix
// Let i be the FirstNonZeroBsplineIndex and
// t be the parameter value, k the order of the
// knot vector, r the DerivativeRequest :
//
// B (t) B (t) B (t)
// i i+1 i+k-1
//
// (1) (1) (1)
// B (t) B (t) B (t)
// i i+1 i+k-1
//
//
//
//
// (r) (r) (r)
// B (t) B (t) B (t)
// i i+1 i+k-1
//
Standard_Integer
ReturnCode,
ii,
pp,
qq,
ss,
NumPoles,
LocalRequest ;
// ,Index ;
Standard_Real NewParameter,
Inverse,
Factor,
LocalInverse,
Saved ;
// , *FlatKnotsArray ;
ReturnCode = 0 ;
FirstNonZeroBsplineIndex = 0 ;
LocalRequest = DerivativeRequest ;
if (DerivativeRequest >= Order) {
LocalRequest = Order - 1 ;
}
if (BsplineBasis.LowerCol() != 1 ||
BsplineBasis.UpperCol() < Order ||
BsplineBasis.LowerRow() != 1 ||
BsplineBasis.UpperRow() <= LocalRequest) {
ReturnCode = 1;
goto FINISH ;
}
NumPoles = FlatKnots.Upper() - FlatKnots.Lower() + 1 - Order ;
BSplCLib::LocateParameter(Order - 1,
FlatKnots,
Parameter,
Standard_False,
Order,
NumPoles+1,
ii,
NewParameter) ;
FirstNonZeroBsplineIndex = ii - Order + 1 ;
BsplineBasis(1,1) = 1.0e0 ;
LocalRequest = DerivativeRequest ;
if (DerivativeRequest >= Order) {
LocalRequest = Order - 1 ;
}
for (qq = 2 ; qq <= Order - LocalRequest ; qq++) {
BsplineBasis(1,qq) = 0.0e0 ;
for (pp = 1 ; pp <= qq - 1 ; pp++) {
//
// this should be always invertible if ii is correctly computed
//
Factor = (Parameter - FlatKnots(ii - qq + pp + 1))
/ (FlatKnots(ii + pp) - FlatKnots(ii - qq + pp + 1)) ;
Saved = Factor * BsplineBasis(1,pp) ;
BsplineBasis(1,pp) *= (1.0e0 - Factor) ;
BsplineBasis(1,pp) += BsplineBasis(1,qq) ;
BsplineBasis(1,qq) = Saved ;
}
}
for (qq = Order - LocalRequest + 1 ; qq <= Order ; qq++) {
for (pp = 1 ; pp <= qq - 1 ; pp++) {
BsplineBasis(Order - qq + 2,pp) = BsplineBasis(1,pp) ;
}
BsplineBasis(1,qq) = 0.0e0 ;
for (ss = Order - LocalRequest + 1 ; ss <= qq ; ss++) {
BsplineBasis(Order - ss + 2,qq) = 0.0e0 ;
}
for (pp = 1 ; pp <= qq - 1 ; pp++) {
Inverse = 1.0e0 / (FlatKnots(ii + pp) - FlatKnots(ii - qq + pp + 1)) ;
Factor = (Parameter - FlatKnots(ii - qq + pp + 1)) * Inverse ;
Saved = Factor * BsplineBasis(1,pp) ;
BsplineBasis(1,pp) *= (1.0e0 - Factor) ;
BsplineBasis(1,pp) += BsplineBasis(1,qq) ;
BsplineBasis(1,qq) = Saved ;
LocalInverse = (Standard_Real) (qq - 1) * Inverse ;
for (ss = Order - LocalRequest + 1 ; ss <= qq ; ss++) {
Saved = LocalInverse * BsplineBasis(Order - ss + 2, pp) ;
BsplineBasis(Order - ss + 2, pp) *= - LocalInverse ;
BsplineBasis(Order - ss + 2, pp) += BsplineBasis(Order - ss + 2,qq) ;
BsplineBasis(Order - ss + 2,qq) = Saved ;
}
}
}
FINISH :
return (ReturnCode) ;
}
函数的作用是用来计算所有的基函数及其导数，并将结果以矩阵（数组）的形式保存。结合二次基函数的推导方法，将述代码写成公式的形式。函数的参数及其描述如下表所示：
|
变量 |
描述 |
|
DerivativeRequest |
导数的次数 |
|
Order |
B样条基函数的阶数(次数+1) |
|
FlatKnots |
节点矢量 |
|
Parameter |
参数 |
|
FirstNonZeroBspline |
第一个非零基函数的索引值 |
|
BsplineBasis |
基函数值矩阵 |
当导数次数DerivativeRequest大于B样条基的阶数Order时，将计算导数的次数设置为B样条基的次数（Order-1）。程序代码如下所示：
LocalRequest = DerivativeRequest ;
if (DerivativeRequest >= Order) {
LocalRequest = Order - 1 ;
}
对B样条基数计算结果矩阵BsplineBasis存储空间进行检查。若存储空间不足，则会退出，程序代码如下所示：
if (BsplineBasis.LowerCol() != 1 ||
BsplineBasis.UpperCol() < Order ||
BsplineBasis.LowerRow() != 1 ||
BsplineBasis.UpperRow() <= LocalRequest) {
ReturnCode = 1;
goto FINISH ;
}
确定参数Parameter所在的节点区间的下标（索引值），程序代码如下所示：
NumPoles = FlatKnots.Upper() - FlatKnots.Lower() + 1 - Order ;
BSplCLib::LocateParameter(Order - 1,
FlatKnots,
Parameter,
Standard_False,
Order,
NumPoles+1,
ii,
NewParameter) ;
确定参数Parameter所在区间的算法是用二分法搜索得到。程序代码如下所示：
//=======================================================================
//function : Hunt
//purpose :
//=======================================================================
void BSplCLib::Hunt (const Array1OfReal& XX,
const Standard_Real X,
Standard_Integer& Ilc)
{
// replaced by simple dichotomy (RLE)
Ilc = XX.Lower();
const Standard_Real *px = &XX(Ilc);
px -= Ilc;
if (X < px[Ilc]) {
Ilc--;
return;
}
Standard_Integer Ihi = XX.Upper();
if (X > px[Ihi]) {
Ilc = Ihi + 1;
return;
}
Standard_Integer Im;
while (Ihi - Ilc != 1) {
Im = (Ihi + Ilc) >> 1;
if (X > px[Im]) Ilc = Im;
else Ihi = Im;
}
}
确定参数所在区间[ui,ui+1)后，可得到第一个非零基函数的索引值为i-p；
FirstNonZeroBsplineIndex = ii - Order + 1 ;
基函数计算的主要算法代码如下所示：
BsplineBasis(1,1) = 1.0e0 ;
for (qq = 2 ; qq <= Order - LocalRequest ; qq++) {
BsplineBasis(1,qq) = 0.0e0 ;
for (pp = 1 ; pp <= qq - 1 ; pp++) {
//
// this should be always invertible if ii is correctly computed
//
Factor = (Parameter - FlatKnots(ii - qq + pp + 1))
/ (FlatKnots(ii + pp) - FlatKnots(ii - qq + pp + 1)) ;
Saved = Factor * BsplineBasis(1,pp) ;
BsplineBasis(1,pp) *= (1.0e0 - Factor) ;
BsplineBasis(1,pp) += BsplineBasis(1,qq) ;
BsplineBasis(1,qq) = Saved ;
}
}
其中：
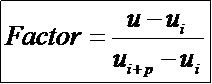为节点区间[ui,ui+1)上的基函数左边部分的系数；
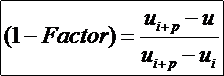为节点区间[ui-1,ui)上的基函数右边部分的系数；
六、 程序示例 Sample Codes
将上述内容以一个简单示例程序来验证，程序代码如下所示：
/*
* Copyright (c) 2013 eryar All Rights Reserved.
*
* File : Main.cpp
* Author : eryar@163.com
* Date : 2013-03-09
* Version :
*
* Description : Learn the B-Spline Curve library in the Open Cascade.
*
*/
#include <BSplCLib.hxx>
#include <math_Matrix.hxx>
#include <TColStd_Array1OfReal.hxx>
#include <TColStd_Array1OfInteger.hxx>
#include <Geom2d_BSplineCurve.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKG2d.lib")
int main(int argc, char* argv[])
{
// Knot vector: [0,0,0,1,2,3,4,4,5,5,5]
TColStd_Array1OfReal knotSeq(1, 11);
knotSeq.Init(0);
knotSeq.SetValue(1, 0);
knotSeq.SetValue(2, 0);
knotSeq.SetValue(3, 0);
knotSeq.SetValue(4, 1);
knotSeq.SetValue(5, 2);
knotSeq.SetValue(6, 3);
knotSeq.SetValue(7, 4);
knotSeq.SetValue(8, 4);
knotSeq.SetValue(9, 5);
knotSeq.SetValue(10, 5);
knotSeq.SetValue(11, 5);
cout<<"Knot Sequence: [ ";
for (Standard_Integer i = 1; i <= knotSeq.Length(); i++)
{
cout<<knotSeq.Value(i)<<" ";
}
cout<<"]"<<endl;
Standard_Integer knotsLen = BSplCLib::KnotsLength(knotSeq);
TColStd_Array1OfReal knots(1, knotsLen);
TColStd_Array1OfInteger mults(1, knotsLen);
// Test Knots, Mults and Knot sequence of BSplCLib.
BSplCLib::Knots(knotSeq, knots, mults);
cout<<"Knots: [ ";
for (Standard_Integer i = 1; i <= knots.Length(); i++)
{
cout<<knots.Value(i)<<" ";
}
cout<<"]"<<endl;
cout<<"Multiplicity: [ ";
for (Standard_Integer i = 1; i <= mults.Length(); i++)
{
cout<<mults.Value(i)<<" ";
}
cout<<"]"<<endl;
if (BSplCLib::KnotForm(knots, 1, knotsLen) == BSplCLib_Uniform)
{
cout<<"Knots is uniform."<<endl;
}
else
{
cout<<"Knots is non-uniform."<<endl;
}
Standard_Real rValue = 2.5;
Standard_Integer iOrder = 2+1;
Standard_Integer iFirstNonZeroIndex = 0;
math_Matrix bSplineBasis(1, 1, 1, iOrder, 0);
BSplCLib::EvalBsplineBasis(1, 0, iOrder, knotSeq, rValue, iFirstNonZeroIndex, bSplineBasis);
cout<<"First Non-Zero Basis index: "<<iFirstNonZeroIndex<<endl;
cout<<bSplineBasis<<endl;
return 0;
}
上述代码对节点矢量、重复度的概念的验证，并以一个实例计算所有非零基函数的值。程序输出为：
Knot Sequence: [ 0 0 0 1 2 3 4 4 5 5 5 ]
Knots: [ 0 1 2 3 4 5 ]
Multiplicity: [ 3 1 1 1 2 3 ]
Knots is uniform.
First Non-Zero Basis index: 3
math_Matrix of RowNumber = 1 and ColNumber = 3
math_Matrix ( 1, 1 ) = 0.125
math_Matrix ( 1, 2 ) = 0.75
math_Matrix ( 1, 3 ) = 0.125
Press any key to continue . . .
七、 结论 Conclusion
通过学习《The NURBS Book》并给合Open Cascade的源程序，理论联系实际，使对NURBS的学习更轻松。
根据B样条基的递推公式，B样条曲线的局部性是通过节点来具体实现的。与Bezier曲线不同的就是增加了节点这个参数。根据Cox-deBoor递推公式亲自推导出一次、二次、三次B样条基函数，可以加深对B样条曲线的理解。
计算给定节点矢量、次数及参数，计算参数所在区间上所有非零基函数算法的步骤为：
l 通过二分法查找出参数所在的节点区间；
l 根据B样条基的局部支撑性，计算出所在节点区间上所有非零基函数；
八、 致谢 Acknowledgments
感谢晓天的支持与鼓励。
九、 参考文献 Bibliography
1． 赵罡，穆国旺，王拉柱译Les Piegl，Wayne Tiller The NURBS Book(Second Edition) 2010 清华大学出版社
2． 莫容，常智勇 计算机辅助几何造型技术 2009 科学出版社
3． 王仁宏，李崇君，朱春钢 计算几何教程 2008 科学出版社