Visualize Surface by Delaunay Triangulator
eryar@163.com
Abstract. Delaunay Triangulation is the core algorithm for mesh generation. By Delaunay Triangulator you can make a general method to visualize geometry surfaces, so does OpenCascade. The paper focus on the geometry surfaces visualization, include the surfaces with holes.
Key words. OpenCascade, Delaunay Triangulator, OpenSceneGraph, Mesh, NURBS
1. Introduction
模型数据最终要在显示器上输出,需要有统一的处理方法。对于曲线而言,只需要在曲线上取一定的点连接成线,就可以用来逼近显示曲线了。对于曲面而言,可以用三角网格来逼近曲面。对于参数表示的曲线,求曲线的点很容易,只要给出参数就可以得到参数对应的曲线上的点。对于参数表示的曲面,情况要复杂些了,如何得到三角网格呢?
经过boolean operation后,会有些孔产生,这些面上的孔如何用统一的方法可视化呢?对于曲面的可视化也一定存在统一、简单的方法。程序开发最终追求的都是简单、统一,这样代码才显得优雅。如果代码看上去很复杂,到处是重复代码,暴露出来的接口也很随意,完全违背单一职责原则和Demeter法则,开发出来的软件用起来必定也很麻烦,这对程序员和软件用户都是噩梦。这样的代码一定有重构和改进的空间,最终达到程序开发人员和软件的用户都舒服的状态。书山有路勤为径,学海无涯苦作舟,拒绝保守、懒惰,不思进取。
言归正传,本文主要使用OpenSceneGraph中的Delaunay Triangulator来对OpenCascade中的任意参数曲面可视化,即曲面可视化的统一算法。在理解曲面可视化的基础上,可对NURBS曲面的可视化,有助于直观来学习NURBS理论。
谈到NURBS理论,又是追求统一、简单的产物。由于在数学和算法上的良好性质,以及在工业领域的成功应用,使得NURBS得到了极大的普及。NURBS在CAD/CAM/CAE领域中所起的作用类似于英语在科学和商业中的作用。因此,想从事CAD,必须理解NURBS。NURBS的重要作用就是统一了曲线曲面的数学模型,使软件对曲线曲面的处理方式相同,且利用NURBS进行设计非常直观,几乎每个工具和算法都有一个易于理解的几何解释。
让CAD软件用户使用简单,得到便利,就要有相应的技术(NURBS)支持。至于NURBS是Non-Uniform Rational B-Spline还是Nobody Understands Rational B-Spline,普通用户是不关心的。网格化的算法也是类似,让三维模型可视化变得简单、统一,至于是使用Delaunay Triangulation还是其他算法,对于图形显示接口如OpenGL也不关心,他只管画三角形就好。然而高效的网格化算法也是一个技术难点。如果不仅要知其然而且还要知其所以然,都要付出努力。
2. Visualize Geometry Surface
网格生成技术是研究如何将给定的空间离散为简单的几何单元的方法。三角网格和四面体网格是迄今为止最为常用的非结构形式,它可以很好地逼近边界,描述结构复杂的空间。Delaunay三角、四面体剖分由于其具有良好的数学基础,对网格的局部控制能力强,网格单元自动向正三角、四面体逼近等优良特性,近年来受到了众多领域的研究人员的关注,在科学计算可视化、图形学三维表示、石油地质勘探、地理信息系统、逆向工程、医学图像处理等领域有着明显的应用前景。
在数字地形建模中,不规则三角网(TIN)通过从不规则离散分布的数据点生成的连续三角面来逼近地形表面。就表达地形信息角度而言,TIN模型的优点是它能以不同层次的分辨率来描述地形表面。TIN模型在一定特定分辨率下能用更少的空间和时间更精确地表示复杂的表面。特别是当地形包含有大量特征,如断裂线、构造线时,TIN模型能更好地顾及这些特征,从而更精确地表达地表形态。关于Delaunay算法,可以参考相关书籍或网络资源自己实现,或是使用开源库,如Triangle, CGAL等。本文主要是使用OpenSceneGraph中现成算法来将参数曲面可视化。
OpenSceneGraph中Delaunay的使用非常简单,只需要将点集传给DelaunayTriangulator即可,下面代码示例将OpenCascade中任意参数曲面的参数空间离散成三角网格,再映射到三维空间,将曲面可视化。
osg::Node* BuildSurface(const Handle_Geom_Surface &theSurface)
{
osg::ref_ptr<osg::Geode> aGeode = new osg::Geode();
osg::ref_ptr<osg::Geometry> aGeometry = new osg::Geometry();
osg::ref_ptr<osg::Vec3Array> aUVPoints = new osg::Vec3Array();
osg::ref_ptr<osg::Vec3Array> aPoints = new osg::Vec3Array();
osg::ref_ptr<osgUtil::DelaunayTriangulator> dt = new osgUtil::DelaunayTriangulator();
// build triangulation for the parametric space.
Standard_Real u1 = 0.0;
Standard_Real u2 = 0.0;
Standard_Real v1 = 0.0;
Standard_Real v2 = 0.0;
theSurface->Bounds(u1, u2, v1, v2);
Precision::IsNegativeInfinite(u1) ? u1 = -1.0: u1;
Precision::IsPositiveInfinite(u2) ? u2 = 1.0: u2;
Precision::IsNegativeInfinite(v1) ? v1 = -1.0: v1;
Precision::IsPositiveInfinite(v2) ? v2 = 1.0: v2;
// tesselate the parametric space.
Standard_Integer aStep = 30;
Standard_Real uDelta = (u2 - u1) / aStep;
Standard_Real vDelta = (v2 - v1) / aStep;
for (Standard_Integer i = 0; i <= aStep; ++i)
{
for (Standard_Integer j = 0; j <= aStep; ++j)
{
Standard_Real u = u1 + i * uDelta;
Standard_Real v = v1 + j * vDelta;
aUVPoints->push_back(osg::Vec3(u, v, 0.0));
}
}
// triangulate the parametric space.
dt->setInputPointArray(aUVPoints);
dt->triangulate();
for (osg::Vec3Array::const_iterator j = aUVPoints->begin(); j != aUVPoints->end(); ++j)
{
// evaluate the point on the surface
gp_Pnt aPoint = theSurface->Value((*j).x(), (*j).y());
aPoints->push_back(osg::Vec3(aPoint.X(), aPoint.Y(), aPoint.Z()));
}
//aGeometry->setVertexArray(aUVPoints);
aGeometry->setVertexArray(aPoints);
aGeometry->addPrimitiveSet(dt->getTriangles());
aGeode->addDrawable(aGeometry);
// use smoothing visitor to set the average normals
osgUtil::SmoothingVisitor sv;
sv.apply(*aGeode);
// set material for the surface
osg::ref_ptr<osg::StateSet> aStateSet = aGeode->getOrCreateStateSet();
osg::ref_ptr<osg::Material> aMaterial = new osg::Material();
aMaterial->setDiffuse(osg::Material::FRONT, osg::Vec4(1.0f, 1.0f, 0.0f, 1.0f));
aMaterial->setSpecular(osg::Material::FRONT, osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f));
aMaterial->setShininess(osg::Material::FRONT, 100.0f);
aStateSet->setAttribute(aMaterial);
return aGeode.release();
}
为了与另一篇blog中的区别,在OpenSceneGraph中绘制OpenCascade的曲面: http://www.cppblog.com/eryar/archive/2013/08/11/202466.html
特意加上了材质和光照效果。离散的曲面效果如下图所示:
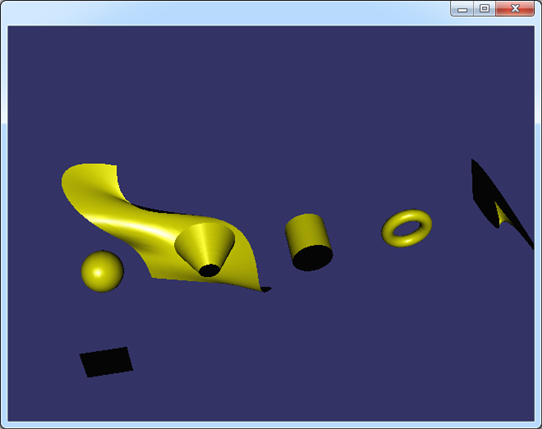
Figure 2.1 Shaded Surfaces in OpenSceneGraph
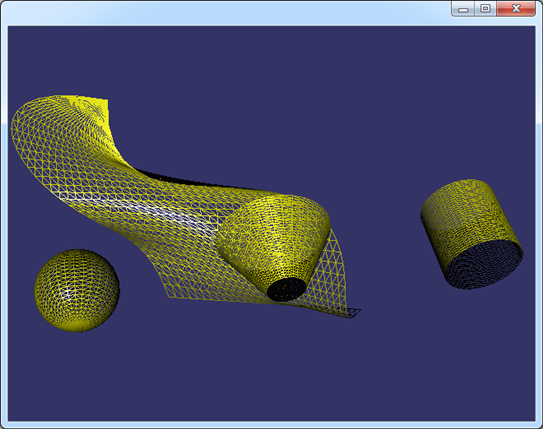
Figure 2.2 Mesh of the Surfaces in OpenSceneGraph
为了显示出光照效果,使用了osgUtil::SmoothingVisitor来自动计算三角网格的平均法向。从上图可知,这种方式是将曲面的参数空间均匀剖分得到的曲面,当剖分得密时,数据量大,但显示得逼真。剖分疏时,数据量小,显示失真。
利用特征敏感网格重剖技术,可以使用较少的三角面片来比较精确地表示几何模型,如下图所示:(图片来源:http://cg.cs.tsinghua.edu.cn/papers/TVCG2007featuresensitive.pdf)
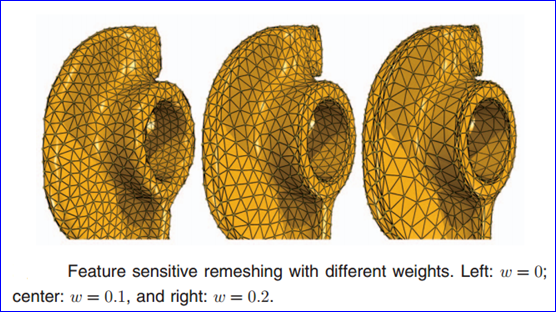
Figure 2.3 Feature sensitive remeshing (http://cg.cs.tsinghua.edu.cn/)
3. Holes in the Surface
当曲面上有开孔时,开孔的信息可以通过WIRE来获得。对于组成开孔的WIRE的每条EDGE,可以通过曲面上的曲线PCurve来将开孔的参数统一到曲面的UV参数空间。
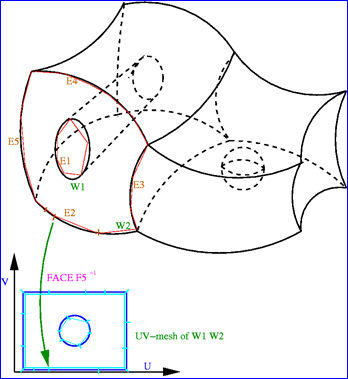
Figure 3.1 Hole in Parametric UV space
在OpenSceneGraph中实现代码如下所示:
osg::Node* BuildSurface(const Handle_Geom_Surface &theSurface, const Handle_Geom2d_Curve &thePCurve)
{
osg::ref_ptr<osg::Geode> aGeode = new osg::Geode();
osg::ref_ptr<osg::Geometry> aGeometry = new osg::Geometry();
osg::ref_ptr<osg::Vec3Array> aUVPoints = new osg::Vec3Array();
osg::ref_ptr<osg::Vec3Array> aPoints = new osg::Vec3Array();
osg::ref_ptr<osg::Vec3Array> aBounds = new osg::Vec3Array();
osg::ref_ptr<osgUtil::DelaunayTriangulator> dt = new osgUtil::DelaunayTriangulator();
osg::ref_ptr<osgUtil::DelaunayConstraint> dc = new osgUtil::DelaunayConstraint();
// build triangulation for the parametric space.
Standard_Real u1 = 0.0;
Standard_Real u2 = 0.0;
Standard_Real v1 = 0.0;
Standard_Real v2 = 0.0;
theSurface->Bounds(u1, u2, v1, v2);
Precision::IsNegativeInfinite(u1) ? u1 = -1.0: u1;
Precision::IsPositiveInfinite(u2) ? u2 = 1.0: u2;
Precision::IsNegativeInfinite(v1) ? v1 = -1.0: v1;
Precision::IsPositiveInfinite(v2) ? v2 = 1.0: v2;
// tesselate the parametric space.
Standard_Integer aStep = 30;
Standard_Real uDelta = (u2 - u1) / aStep;
Standard_Real vDelta = (v2 - v1) / aStep;
for (Standard_Integer i = 0; i <= aStep; ++i)
{
for (Standard_Integer j = 0; j <= aStep; ++j)
{
Standard_Real u = u1 + i * uDelta;
Standard_Real v = v1 + j * vDelta;
aUVPoints->push_back(osg::Vec3(u, v, 0.0));
}
}
Standard_Real pDelta = (thePCurve->LastParameter() - thePCurve->FirstParameter()) / aStep;
for (Standard_Integer c = 0; c <= aStep; ++c)
{
gp_Pnt2d p = thePCurve->Value(thePCurve->FirstParameter () + c * pDelta);
aBounds->push_back(osg::Vec3(p.X(), p.Y(), 0.0));
}
dc->setVertexArray(aBounds);
dc->addPrimitiveSet(new osg::DrawArrays(osg::PrimitiveSet::LINE_LOOP, 0, aBounds->size()));
// triangulate the parametric space.
dt->addInputConstraint(dc);
dt->setInputPointArray(aUVPoints);
dt->triangulate();
dt->removeInternalTriangles(dc);
for (osg::Vec3Array::const_iterator j = aUVPoints->begin(); j != aUVPoints->end(); ++j)
{
// evaluate the point on the surface
gp_Pnt aPoint = theSurface->Value((*j).x(), (*j).y());
aPoints->push_back(osg::Vec3(aPoint.X(), aPoint.Y(), aPoint.Z()));
}
//aGeometry->setVertexArray(aUVPoints);
aGeometry->setVertexArray(aPoints);
aGeometry->addPrimitiveSet(dt->getTriangles());
aGeode->addDrawable(aGeometry);
// use smoothing visitor to set the average normals
osgUtil::SmoothingVisitor sv;
sv.apply(*aGeode);
// set material for the surface
osg::ref_ptr<osg::StateSet> aStateSet = aGeode->getOrCreateStateSet();
osg::ref_ptr<osg::Material> aMaterial = new osg::Material();
aMaterial->setDiffuse(osg::Material::FRONT, osg::Vec4(1.0f, 1.0f, 0.0f, 1.0f));
aMaterial->setSpecular(osg::Material::FRONT, osg::Vec4(1.0f, 1.0f, 1.0f, 1.0f));
aMaterial->setShininess(osg::Material::FRONT, 100.0f);
aStateSet->setAttribute(aMaterial);
return aGeode.release();
}
开孔的实现主要也是用osgUtil::DelaunayConstraint,将孔中的三角形去除。如下图所示为在球面和锥面开孔:
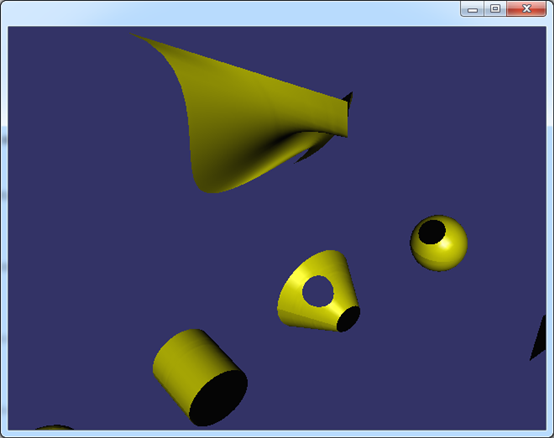
Figure 3.2 Holes on Sphere and Cone Surface
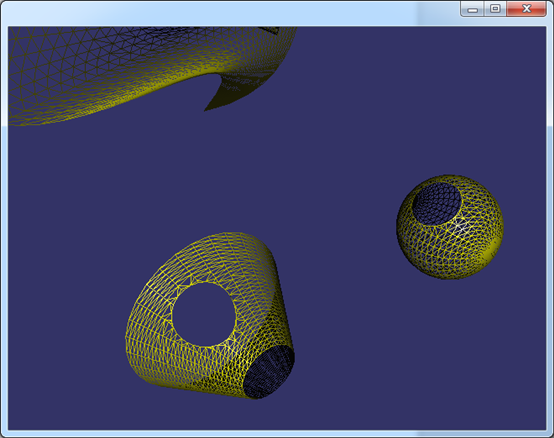
Figure 3.3 Mesh for Sphere and Cone with holes
由上图可知,对于有拓朴结构的三维模型数据,可以由WIRE得到组成孔的每条边Edge,根据Edge中PCurve可以找到对应的曲面。通过PCurve将开孔数据统一到参数空间中。剖分完带孔的参数空间,再映射回三维空间就得到开孔的曲面了。
4. Conclusion
原来一直百思不得其解的问题现在已经豁然开朗,对三维模型的可视化有了一定的理解。借助于这些开源库,对相关知识的学习要轻松许多,可以将许多国产教材上断续的理论知识与实践衔接起来。
5. Acknowledgement
感谢OpenCascade和OpenSceneGraph的开放和分享,让学习变得轻松有趣。
6. Reference
1. 孙家广, 胡事民等. 计算机图形学. 清华大学出版社. 2000
2. 赵罡, 穆国旺, 王拉柱译. 非均匀有理B样条. 清华大学出版社. 2010
3. Jonathan R. Shewchuk. Triangle: http://www.cs.cmu.edu/~quake/triangle.html
4. 汪嘉业 王文平 屠长河 杨承磊. 计算几何及应用. 科学出版社. 2011
5. 王成恩. 面向科学计算的网格划分与可视化技术. 科学出版社. 2011
6. 周培德. 计算几何-算法设计与分析. 清华大学出版社. 2008
7. http://cg.cs.tsinghua.edu.cn/
8. Mesh Algorithm in OpenCascade:
http://www.cppblog.com/eryar/archive/2014/04/06/206484.html