Make Helix Curve in OpenCASCADE
eryar@163.com
Abstract. OpenCASCADE does not provide helix curve directly, but you can build a helix curve by the pcurve of a surface(curve on surface). When you understand the pcurve of a surface, you can make a helix curve easily. The paper first make a helix by Tcl in Draw Test Harness, then translate the Tcl script to OpenCASCADE C++ code.
Key Words. OpenCASCADE, Helix Curve, PCurve, Sweep, Spring
1. Introduction
螺旋线是实践中常用到的曲线,例如平头螺丝钉的外缘曲线就是螺旋线。当我们拧紧平头螺丝钉时,它的外缘曲线上的任一点M一方面绕螺丝钉的轴旋转,另一方面又沿平行于轴线的方向前进,点M就走出一段螺旋线。[1]
如果空间一点M在圆柱面x*x+y*y=a*a上以角速度ω绕z轴旋转,同时又以线速度υ沿平等于z轴正方向上升(其中ω,υ都是常数),那未点M构成的图形叫螺旋线。其参数方程为:
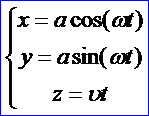
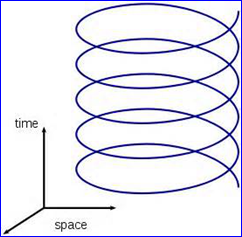
Figure 1.1 A Helix Curve
OpenCASCADE中并没有直接提供构造螺旋线的类和函数,因此只有自己来构造了,其中构造的核心是要理解PCurve(曲面的参数曲线)。本文先以Tcl脚本在Draw Test Harness中快速生成一个螺旋线,再将相应的Tcl脚本转换成C++代码。在理解Pcurve概念的基础上来构造螺旋线还是很简单的,甚至还可以扩展应用。
2.Make Helix Curve
在OpenCASCADE提供的一个经典例子:生成一个酒瓶中,就有螺旋线的应用,即生成瓶口处的螺纹。当时看这例子的时候也是没有完全理解,究竟怎么生成的那个螺旋线?感谢lifenli的提醒,使我又重温了一遍例子,顿时茅塞顿开,明白了pcurve的一个应用。
由《OpenCASCADE BRep Format》[4]中可知,圆柱面的参数方程为:
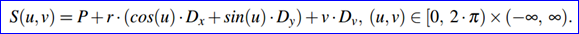
假设当你在参数空间[u,v]中创建一条二维曲线后,可根据这个二维曲线来计算对应曲面上的三维曲线。根据二维曲线的不同定义,得到的结果如下:
条件 | 参数方程 | 参数曲线 |
U=0 | S(v)=P+r*cos(u)+vDz | 与Z轴平行的直线 |
V=0 | S(u)=P+r*(cos(u)*Dx+sin(u)*Dy) | 与XOY面平行的圆 |
U!=0 && V != 0 | S(u,v)=P+r(cos(u)*Dx+sin(u)*Dy)+vDz | 螺旋线 |
对比螺旋线的参数方程可知,当参数空间中的u和v都不为0时,得到的圆柱面上的线就是螺旋线。考虑最简单的情况,那就是u=v,即在参数空间中是一条斜率k=1的直线。在OpenCASCADE的Draw Test Harness用Tcl脚本测试,Tcl脚本如下所示:
#
# make helix curve in OpenCASCADE.
# Shing Liu(eryar@163.com)
# 2015-07-08 22:00
#
pload MODELING VISUALIZATION
cylinder aCylinder 6
line aLine2d 0 0 1 1
trim aSegment aLine2d 0 2*pi
mkedge aHelixEdge aSegment aCylinder 0 6*pi
vdisplay aHelixEdge
代码先加载所需的造型及显示模块,然后创建一个圆柱面aCylinder;一条二维直线aLine2d;再将参数范围限定在0到2PI之间;最后使用了用曲面及其上的pcurve来创建边的算法mkedge生成了螺旋线并显示在三维窗口中。
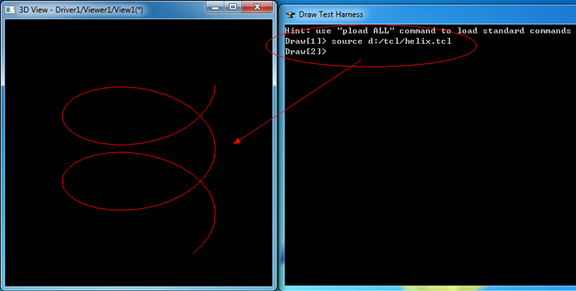
Figure 2.1 Make a helix by Tcl script
上述Tcl脚本可以很容易的转换成C++代码的,下面给出相应的C++实现,源码如下所示:
#define WNT
#include <gp_Lin2d.hxx>
#include <GCE2d_MakeSegment.hxx>
#include <Geom_CylindricalSurface.hxx>
#include <BRepBuilderAPI_MakeEdge.hxx>
#include <TopoDS_Edge.hxx>
#include <BRepTools.hxx>
#pragma comment(lib, "TKernel.lib")
#pragma comment(lib, "TKMath.lib")
#pragma comment(lib, "TKG3d.lib")
#pragma comment(lib, "TKBRep.lib")
#pragma comment(lib, "TKGeomBase.lib")
#pragma comment(lib, "TKTopAlgo.lib")
void makeHelix(void)
{
Handle_Geom_CylindricalSurface aCylinder = new Geom_CylindricalSurface(gp::XOY(), 6.0);
gp_Lin2d aLine2d(gp_Pnt2d(0.0, 0.0), gp_Dir2d(1.0, 1.0));
Handle_Geom2d_TrimmedCurve aSegment = GCE2d_MakeSegment(aLine2d, 0.0, M_PI * 2.0);
TopoDS_Edge aHelixEdge = BRepBuilderAPI_MakeEdge(aSegment, aCylinder, 0.0, 6.0 * M_PI).Edge();
BRepTools::Dump(aHelixEdge, std::cout);
BRepTools::Write(aHelixEdge, "d:/helix.brep");
}
int main(int argc, char* argv[])
{
makeHelix();
return 0;
}
由C++代码可知,生成螺旋线的关键是在生成边的时候,将pcurve和相应的曲面及其参数范围一起传给了生成边的类,这样就得到拓朴边了。如果想要得到几何的螺旋线,可以使用工具BRep_Tool::Curve()来将拓朴边中的几何曲线提取出来。经过测试,用pcurve生成的Edge中没有三维几何曲线,不过occ提供了一个静态函数来将pcurve对应的三维曲线拟合成nurbs曲线,函数为:BRepLib::BuildCurve3d();
参数空间中pcurve的斜率决定了螺旋线的螺距pitch,当其他参数不变,改变斜率后得到如下图所示结果:
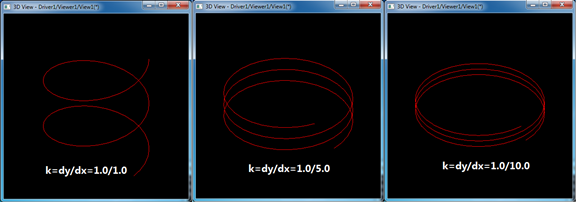
Figure 2.2 Different Pitch by different K
由图可知,当pcurve的斜率越小时,得到的螺旋线的螺距也越小。修改pcurve的斜率只需要修改上述Tcl脚本中的aLine2d的斜率。
如当斜率k=1时的pcurve为:
line aLine2d 0 0 1 1
当斜率k=1.0/5.0时的pcurve为:
line aLine2d 0 0 5 1
当斜率k=1.0/10.0时的pcurve为:
line aLine2d 0 0 10 1
可以自己尝试修改看看没的斜率得到的不同螺旋线的螺距变化。
3.Spring: Sweep profile along helix
得到螺旋线后自然就想到能不能用一个圆沿着螺旋线来放样,从而得到一个弹簧。下面还是用Tcl脚本在Draw Test Harness中尝试一下,相应的C++实现也是很容易找到相关的类。
#
# make helix curve in OpenCASCADE.
# Shing Liu(eryar@163.com)
# 2015-07-08 22:00
#
pload MODELING VISUALIZATION
cylinder aCylinder 6
line aLine2d 0 0 1 1
trim aSegment aLine2d 0 2*pi
mkedge aHelixEdge aSegment aCylinder 0 6*pi
# there is no curve 3d in the pcurve edge.
mkedgecurve aHelixEdge 0.001
wire aHelixWire aHelixEdge
circle profile 6 0 0 0 4 1 1
mkedge profile profile
wire profile profile
mkplane profile profile
pipe aSpring aHelixWire profile
vdisplay aSpring
vsetmaterial aSpring steel
vsetgradientbg 180 200 255 180 180 180 2
vsetdispmode 1
vzbufftrihedron
# set ray tracing
if { ! [catch {vrenderparams -raytrace -shadows -reflections -fsaa -rayDepth 5}] } {
vtextureenv on 1
}
生成效果如下图所示:
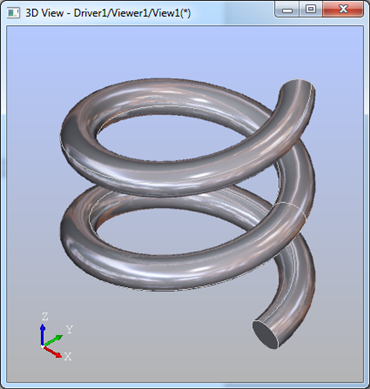
Figure 3.1 Spring by sweep a circle along a helix path
当将pcruve在圆锥面上生成三维曲线时就会得到类似夏天的蚊香那样螺旋形状。同样使用上述代码,只是将圆柱面改成圆锥面得到:
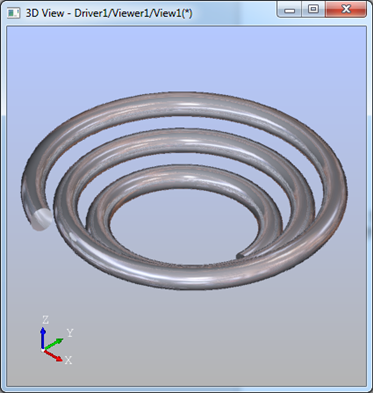
Figure 3.2 Mosquito Coil
4.Conclusion
综上所述,常见的计算几何造型书中讲到曲线的参数方程都会以螺旋线为经典例子,甚至是高等数学中也是一样,由此可见螺旋线是很常见的一种曲线。但是occ中并没有直接提供螺旋线的几何曲线,只有通过pcurve来构造了。所以理解pcurve后,才好理解make bottle例子中的瓶颈螺纹部分的代码。
通过将一个轮廓沿着螺旋线扫掠可以得出很多有意思的模型。在使用sweep的过程中发现pcurve生成的边Edge中并没有三维几何曲线,所以会导致算法失败。最终发现occ提供了一个将pcurve生成的边中生成出一个拟合三维几何曲线的函数BRepLib::BuildCurve3d()。对于一些在曲面上的曲线的造型可以参考这种用法,用pcurve来构造。
5. References
1. 同济大学数学教研室. 高等数学(上). 高等教育出版社. 1978
2. Helix. http://mathworld.wolfram.com/Helix.html
3. OpenCASCADE Make Bottle Tutorial. 2015
4. OpenCASCADE BRep Format. 2015
5. 莫勇,常智勇. 计算机辅助几何造型技术. 科学出版社. 2009