OpenCASCADE曲面交线分类
eryar@163.com
Abstract. OpenCascade classify the intersection line between two surfaces. A intersection line may be either geometric: line, circle, ellipse, parabola, hyperbola as defined in the class GLine, or analytic as defined in the class ALine, or defined by a set of points(coming from a walking algorithm) as defined in the class WLine. Or described by a restriction line on one of the surfaces as RLine.
Key Words. Surface Intersection, Intersection Line
1 Introduction
OpenCASCADE中对两个曲面求交得到的交线进行了分类,如下类图所示:
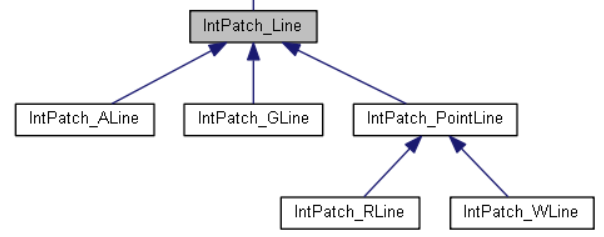
交线总共分为四类:
- ALine:Analytic解析曲线,主要为两个二次曲面求交所得,如圆柱面、球面、圆锥面等之间的交线;
- GLine:Geometric几何曲线,即交线可以表示成简单的二次曲线,如直线、圆、抛物线等;
- WLine:Walking追踪法得到的交线,保存了追踪路线上的两个曲面的交点;
- RLine:Restriction受限交线,这条交线可能只在一个面上;
下面我们使用Tcl脚本在DRAW中验证一下这四类交线的来源,加深对曲面求交算法的理解。分类带来了麻烦,可以带着问题:为什么要分这几种类型?有什么好处?来看这篇文章。要用好开源的东西,其实要求还是很高的,需要对源码有相对深入的理解。
2 ALine
Analytic交线是二次曲面求交所得,二次曲面是因为可以统一使用二次型来表示的解析曲面,也是《解析几何》中研究的主要内容。我们可以在DRAW中构造圆柱面与圆锥面求交验证一下。TCL脚本如下:
# Test for IntPatch_ALine.
# Geometry surfaces.
cylinder s1 0 0 0 1 1 1 2
cone s2 0 0 0 0 0 1 1 0 0 30 3
# Topology faces
mkface f1 s1 0 2*pi -8 8
mkface f2 s2 0 2*pi -5 5
# Intersection.
bop f1 f2
bopsection r
# Display result.
vdisplay f1 f2 r
生成结果如下图所示,其中红色为交线:
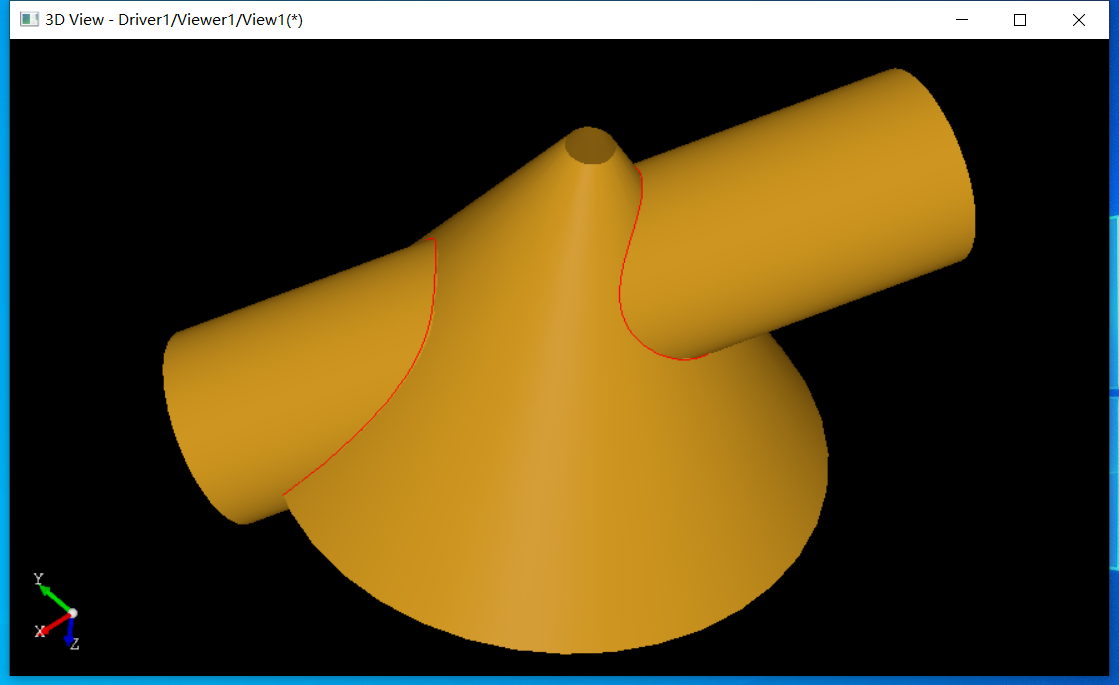
DEBUG源码可以看到是使用类IntPatch_ImpImpIntersection 计算求交,即两个解析曲面求交算法类。

3 GLine
Geometric几何曲线形式简单,如果交线用几何曲线来表示,对于后续算法有好处。如平面与圆锥面求交线,圆柱面与圆柱面求交等,都会得到几何曲线。将上面的圆柱面换成平面与圆锥面求交我们可以在DRAW验证经典的圆锥与平面交线:根据平面位置不同,可以得到圆、椭圆、双曲线等几何曲线。TCL脚本如下所示:
# Test for IntPatch_GLine.
cone s1 0 0 0 0 0 1 30 3
plane s2 0 0 0 0 0 1
mkface f1 s1 0 2*pi -5 5
mkface f2 s2 -8 8 -8 8
bop f1 f2
bopsection r
vdisplay f1 f2 r
计算交线结果如下图所示:

我们改变平面的法向,使其斜着与圆锥面求交,会得到椭圆:
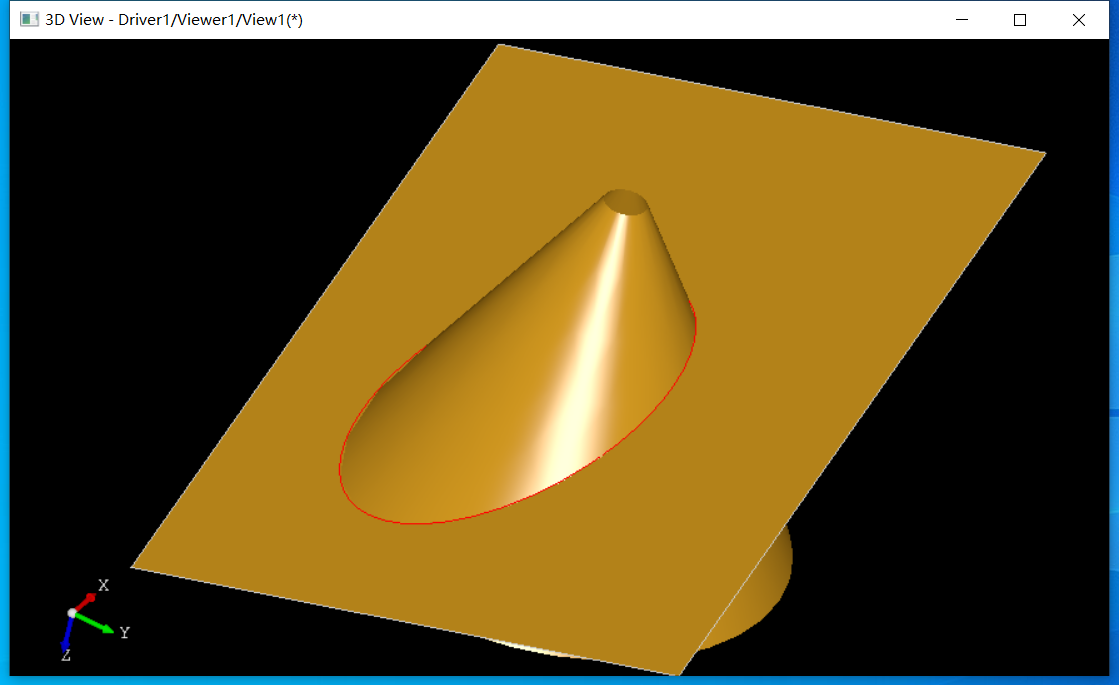
还可以得到双曲线、抛物线等,同学们可以自己尝试一下。
4 WLine
对于NURBS曲面求交,一般会使用Marching方法,国内教材翻译为追踪法。在看《地球脉动》时,注意到对于大草原上的水牛、大象等动物成群结队的迁徙使用了这个词,这个词的字面意思有行进、行军,列队行进之意,如果结合opencascade中的walking感觉翻译为行进法更贴切,因为在opencascade中对于求交专门有个package名为IntWalk,其中类IntWalk_PWalking来使用marching method对两个参数曲面进行求交。Walk有行走之意,所以对于使用Walk方法得到的交线命名为WLine。对于NURBS曲面求交及二次曲面与NURBS曲面求交,使用了Marching方法,WLine的来源是清晰的。继续使用上面的脚本,只需要将上述两个面转换成NURBS曲面即可触发Marching法进行求交。TCL脚本如下:
# Test for IntPatch_WLine.
cone s1 0 0 0 0 0 1 30 3
plane s2 0 0 0 1 1 2
mkface f1 s1 0 2*pi -5 5
mkface f2 s2 -8 8 -8 8
nurbsconvert f1 f1
nurbsconvert f2 f2
bop f1 f2
bopsection r
vdisplay f1 f2 r
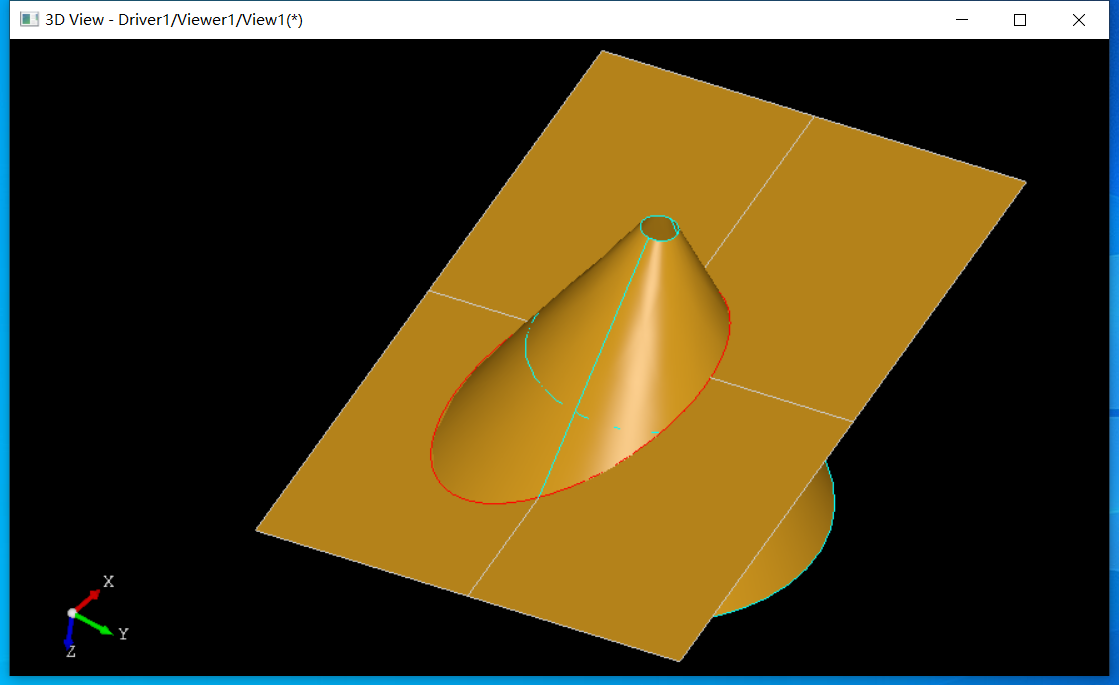
通过IntWalk_PWalking行进法配合三参数迭代法,将行进过程中的交点都保存在WLine中。
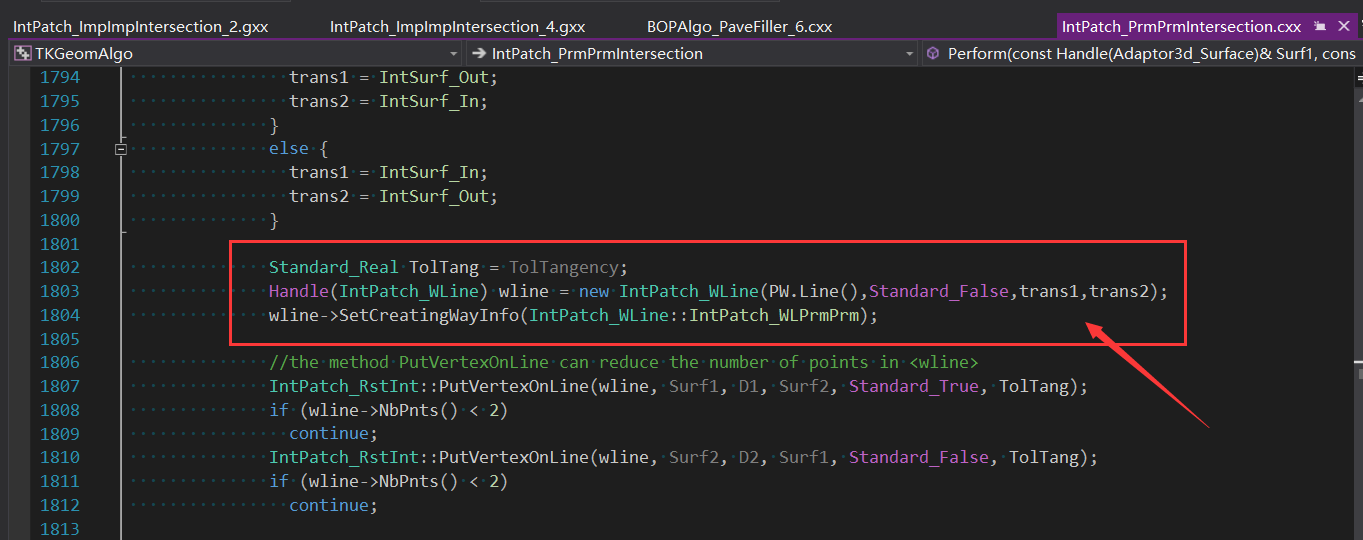
虽然结果与上面看上去一样,内部交线已经不是简单的几何曲线了。
5 RLine
Restriction交线是受限交线,这种类型的交线只会位于一个面上。这里我们构造一个平面及与平面重叠的一个NURBS曲面来求交进行解释。TCL脚本如下:
# Test for IntPatch_RLine.
plane s1 0 0 0 0 0 1
plane s2 0 0 0 0 0 1
mkface f1 s1 -5 5 -5 5
mkface f2 s2 -8 8 -8 8
nurbsconvert f1 f1
bop f1 f2
bopsection r
vdisplay f1 f2 r
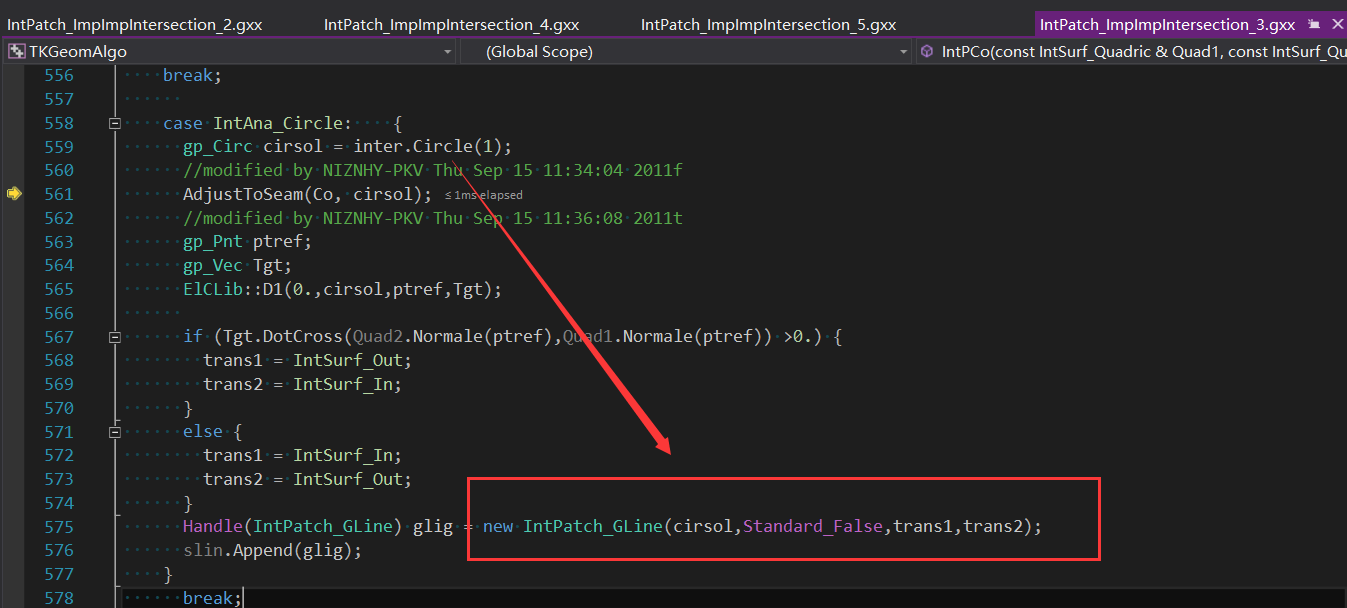
DEBUG会发现这两个曲面的交线为RLine,并在生成RLine时指定交线属于哪个曲面,是在S1曲面SetArcOnS1还是在S2曲面SetArcOnS2:
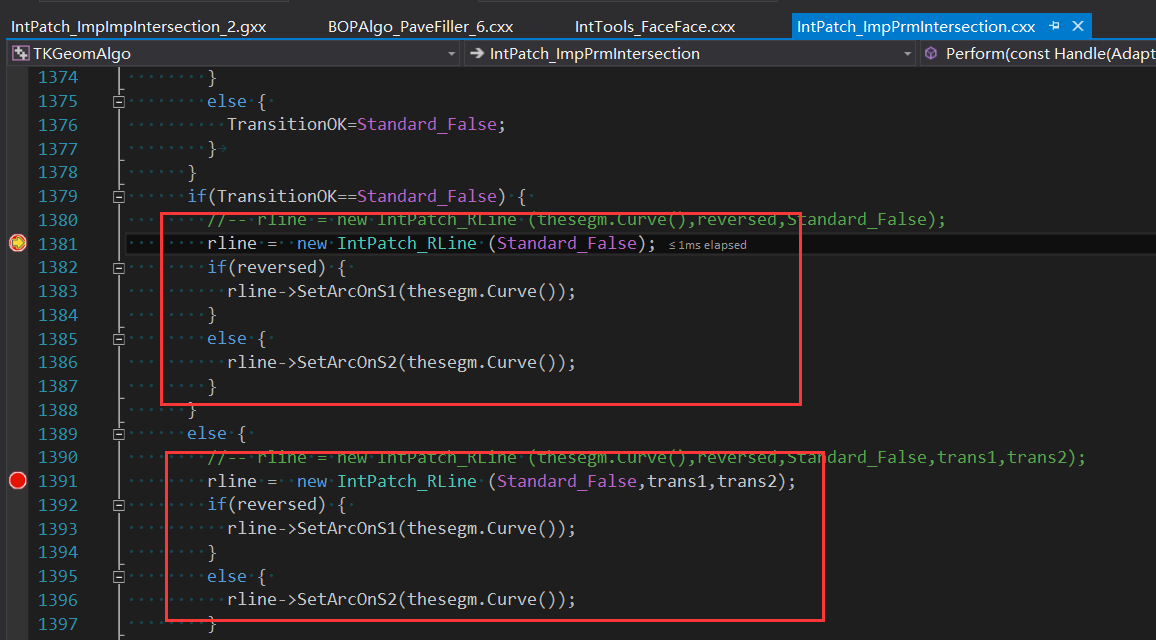
生成交线如下图所示:
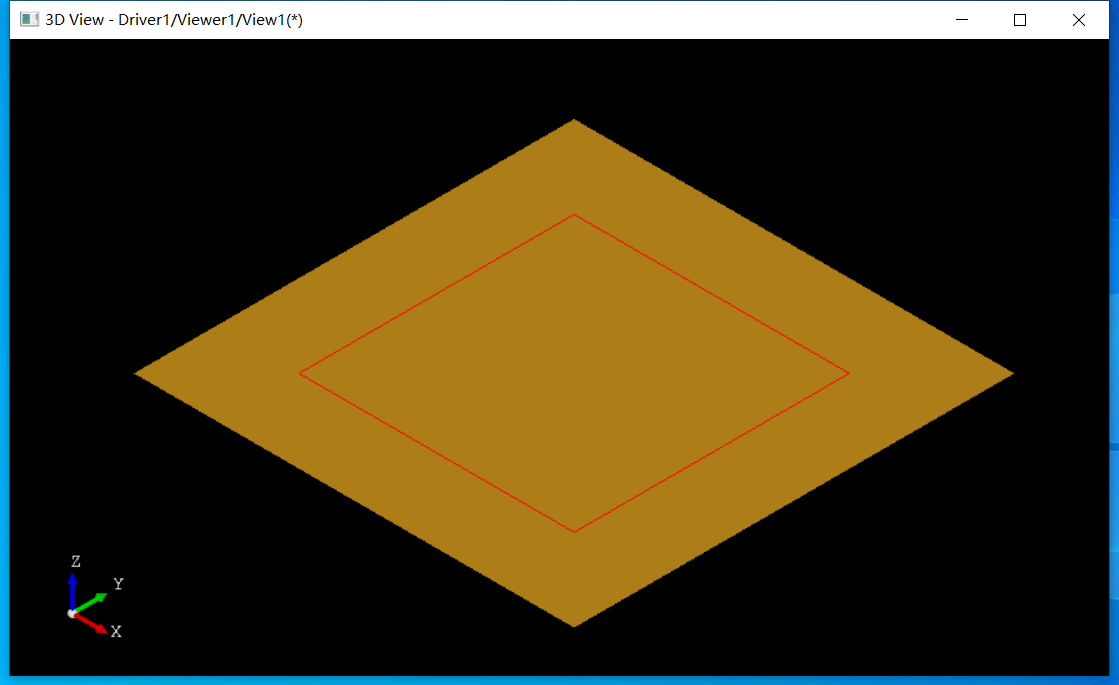
当然可以使用RLine来判断两个曲面是否有重叠,但是在opencascade中两个曲面重叠叫Tangent Face,可以将上述NURBS面不转换,还是使用两个重叠平面来验证:

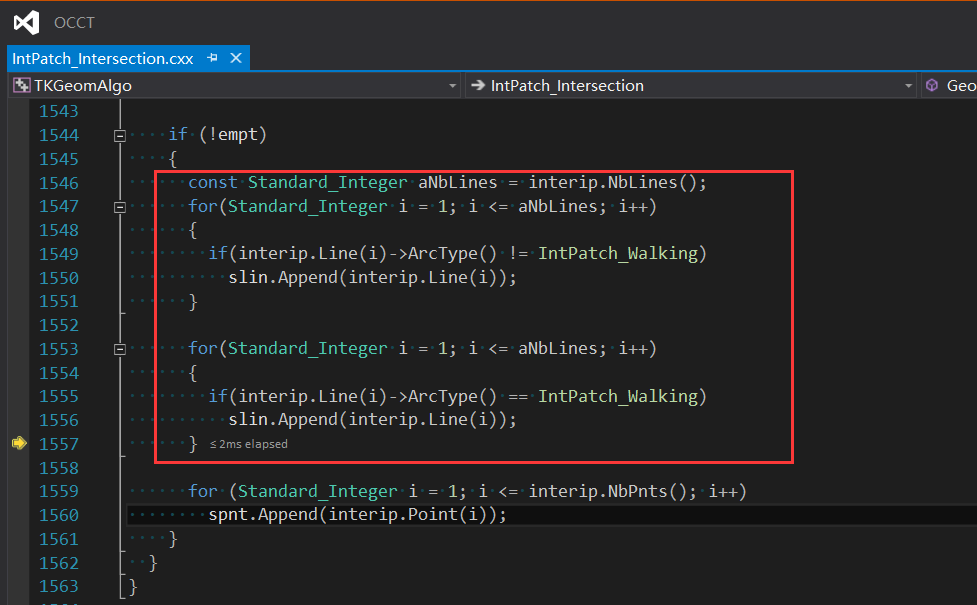
求交最后对交线数据归并时的代码有点不敢恭维:
6 Conclusion
综上所述,对两个曲面求交得到的交线进行分类,避免交线都是NURBS曲线,可以是简单的二次曲线,提高后续算法性能。在理解源码的基础上,可以根据实际应用场景选择高效的算法。如若只是求两个模型之间的交线,可以直接使用曲面求交算法,一般情况下性能还是不错的。当然理解源码后,可以结合实际应用场景可以对求交算法做进一步优化。
要深入理解opencascade源码,熟练使用DRAW是一个相对容易的路线。因为在DRAW中可以使用Tcl脚本快速验证各种想法,甚至直接DEBUG源码,从表向深入到与源码作者直接对话。