《编程之美》读书笔记13: 4.1 金刚坐飞机问题
问题:
现在有一班飞机将要起飞,乘客们正准备按机票号码(1, 2, 3, …N)依次排队登机。突然来了一只大猩猩(对,他叫金刚)。他也有飞机票,但是他插队第一个登上了飞机,然后随意地选了一个座位坐下了1。根据社会的和谐程度,其他的乘客有两种反应:
1. 乘客们都义愤填膺,“既然金刚同志不遵守规定,为什么我要遵守?”他们也随意地找位置坐下,并且坚决不让座给其他乘客。
2. 乘客们虽然感到愤怒,但还是以“和谐”为重,如果自己的位置没有被占领,就赶紧坐下,如果自己的位置已经被别人(或者金刚同志)占了,就随机地选择另一个位置坐下,并开始闭目养神,不再挪动位置。
那么,在这两种情况下,第 i 个乘客(除去金刚同志之外)坐到自己原机票位置的概率分别是多少?
对问题一,每个人都是随机选择座位,任意一个人坐在指定座位的概率相同,因而第i个乘客坐在其座位的概率是 1/n。
对问题二,答案和金刚的原来座位编号有关。不妨先去除金刚的座位,将乘客(根据机票号)和剩下的座位,按原大小顺序从1开始重新编号。用F(i,n)表示在新排列中(共有n-1个乘客座位和金刚原来的座位),新的第i个乘客坐在其原来座位的概率,则在n个座位中:
① 金刚若挑自己的座位或选的座位在第i个座位后(共有n-i个座位满足这个条件),则第i个乘客肯定能坐到原来的座位;
② 金刚若挑选的座位在第i个座位前,不妨假设为j,则第j个乘客除非坐到金刚的座位,不然就会抢其他人的座位,因为他的行为和金刚相似,可以将他当做金刚处理。去除前j个座位,剩下的座位和乘客再按原大小排序重新从1开始编号,则先前的第i个乘客,其座位号变为i-j,新的总座位数变为n-j。因而可得公式:
用 G(i, n)表示原排列中,第i个乘客坐到自己座位的概率,假设金刚的座位编号为j。
若 i<j 则 G(i,n)=F(i,n)= (n-i)/(n+1-i)。
若 i>j 则 G(i,n)=F(i-1,n)= (n+1-i)/(n+2-i) 。
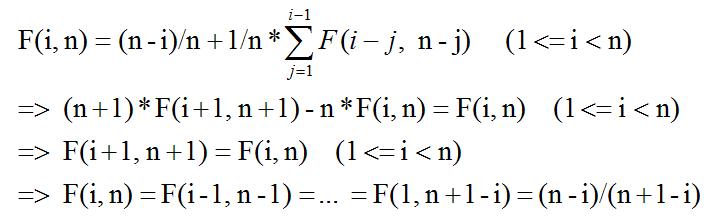
类似题:
“约瑟芬环:n个人,编号为0到n-1,围成一圈,从编号为0的开始,从1开始报数,所有报到m的出列,下一个人从1开始继续报数。求最后一个人的编号。”