问题:寻找数组中的最小值和最大值。
一道很简单的题目,一般有下面4种解法:
1 遍历两次,每次分别找出最小值和最大值。
2 只遍历一次,每次取出的元素先与已找到的最小值比较,再与已找到的最大值比较。
3 每次取两个元素,将较小者与已找到的最小值比较,将较大者与已找到的最大值比较。
4 分治:将数组划分成两半,分别找出两边的最小值、最大值,则最小值、最大值分别是两边最小值的较小者、两边最大值的较大者。
这4种算法,哪种效率最高,哪种最低?
后两种算法只要进行1.5*N次比较,因而网上有不少解答都将它们列为最佳答案。但是,算法4用到了递归,而递归法函数调用的开销是很大的,这就注定了该算法的效率肯定不高。那么,算法3就是最高效的吗?还是用代码来验证吧。
后面的代码,对每种算法都实现了两个函数(假设数组长度为N):
算法1:solve_1a与solve_1b,后者加入两个临时变量,编译器可以将变量储存在寄存器中,不用每次循环都要写内存。比较次数为2*N次。
算法2:solve_2a与solve_2b,前者每次循环必比较2次,后者最好情况下(递减数组)只要比较1次,但最差情况下(递增数组)则要比较2次,比较次数为:N到2 * N次。
算法3:solve_3a与solve_3b,前者每次循环取头尾两元素(从两头往中间取),后者取相邻两元素。比较次数为1.5 * N次。
算法4:solve_4a与solve_4b,后者返回一个结构(只有两个元素),编译器优化可以通过两个寄存器返回该结构,减少写内存次数。(检查gcc产生的汇编,确认有进行该优化)。比较次数为1.5 * N次。
下面是测试结果:(数组长度为6e7,每种算法测4次取平均值)
|
|
所用时间(毫秒,GCC 4.5)
|
所用时间(毫秒,VC 2010)
|
|
函数名
|
递增
|
递减
|
乱序1
|
乱序2
|
乱序3
|
递增
|
递减
|
乱序1
|
乱序2
|
乱序3
|
|
1a 两次遍历
|
175
|
183
|
187
|
179
|
179
|
199
|
203
|
176
|
187
|
175
|
|
1b 两次遍历(优化)
|
175
|
179
|
171
|
171
|
172
|
183
|
234
|
175
|
187
|
172
|
|
2a 一次遍历
|
105
|
105
|
105
|
129
|
105
|
105
|
132
|
105
|
109
|
105
|
|
2b 一次遍历(优化)
|
105
|
90
|
105
|
109
|
105
|
109
|
109
|
105
|
113
|
105
|
|
3a 取头尾两元素
|
85
|
85
|
246
|
246
|
246
|
86
|
82
|
261
|
261
|
261
|
|
3b 取相邻两元素
|
93
|
101
|
238
|
242
|
238
|
93
|
101
|
258
|
257
|
253
|
|
4a 分治法
|
316
|
359
|
867
|
863
|
867
|
773
|
777
|
1554
|
1558
|
1558
|
|
4b 分治法(优化)
|
273
|
289
|
824
|
824
|
828
|
648
|
656
|
1347
|
1340
|
1339
|
编译参数:tdm-gcc 4.5.2-dw2: g++ -O3 -s -Wextra –Wall VC 2010: cl /Ox /EHsc /nologo /W3
很明显,“分治”法的效率远低于其它
3种算法。对前3
种算法,将数组长度增加到1e8
,并对十组随机数组进行测试,得到结果:
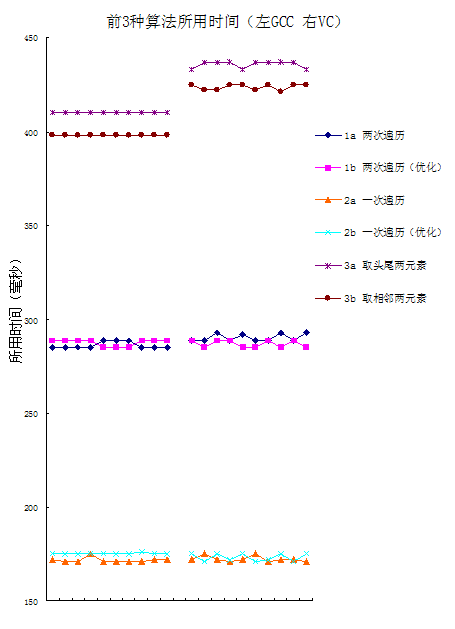
从上面的表和图可以看出,算法3在数组有序时,运行效率很高(但与算法2相差不大),而在乱序时,甚至比两次遍历都慢。乱序时:算法2效率最高,算法1次之,算法3效率最低。
算法2a和算法2b的效率差不多,有时算法2a的效率还略高。算法2a,每次循环都要比较2次,算法2b每次循环要比较1到2次,但由于前者的两次比较是无关的,后者的比较是相关的(第一次比较的结果决定是否进行第二次比较),在现代CPU“指令预测”等技术前,算法2a在某些情况下能比较算法2b更高效。
算法3的效率也不是绝对最差的,上面的随机数组是通过随机产生一些数得到,如果把它改为对数组的元素进行 “随机洗牌”,就得到下面的结果(所得的新数据与上面的数据和并,下图中第一、三列是上面的数据,第二、四列是改用“随机洗牌”后得到的新数据):
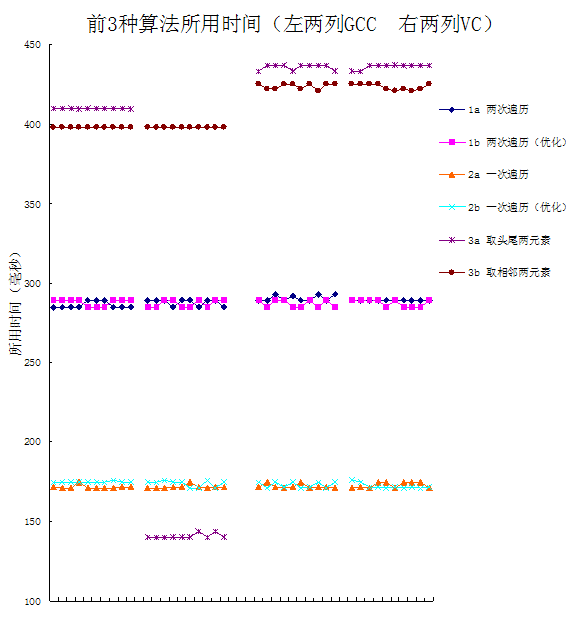
从图可以看出,改用“随机洗牌”法得到乱序数组后,VC的结果没发生改变,GCC除了函数3a,结果也没改变,但是“3a一次取头尾两元素”却成为最高效的算法,但其效率和 “一次遍历取一个元素” 法,相差并不是太大。因而可以说,在单线程环境下,“一次遍历取一个元素”这个最容易想到的方法,反而是本题的最佳解法。
算法上的最优,并不一定是实际上的最优,快排和堆排序就是一个典型的例子,虽然快排最坏情况下的复杂度是O(N^2),而堆排序始终是O(N lgN),但实际运用中,一个好的快排实现一般都比堆排序快很多。何况这4种算法的复杂度还都是O(N)。为了在最坏情况下节省0.5 * N次比较,进行的所谓优化,得到的结果很可能与所期望的恰恰相反。

 找出数组的最小值和最大值
找出数组的最小值和最大值
1
2 // www.cnblogs.com/flyinghearts flyinghearts # qq.com
// www.cnblogs.com/flyinghearts flyinghearts # qq.com
3
4 #include <algorithm>
#include <algorithm>
5 #include <limits>
#include <limits>
6 #include <vector>
#include <vector>
7 #include <cstdio>
#include <cstdio>
8
9 #define NOMINMAX 1
#define NOMINMAX 1
10 #include <windows.h>
#include <windows.h>
11
12 #define TEST_CASE 1 // 第0组还是第1组测试
#define TEST_CASE 1 // 第0组还是第1组测试
13 #define RANDOM_SHUFFLE 0 // 乱序是否通过随机洗牌获得
#define RANDOM_SHUFFLE 0 // 乱序是否通过随机洗牌获得
14
15
16 #define TEST_RAND_POS 0
#define TEST_RAND_POS 0
17 const unsigned Pack = 4; // 对某组数据连续测试Pack次,取平均值
const unsigned Pack = 4; // 对某组数据连续测试Pack次,取平均值
18 const unsigned Rand_M = 5; // 测试某个乱序数组的 Rand_M个子数组
const unsigned Rand_M = 5; // 测试某个乱序数组的 Rand_M个子数组
19 #if ! TEST_CASE
#if ! TEST_CASE
20 const unsigned Fix_M = 3; // 固定数组长度时,测试Fix_M个乱序数组
const unsigned Fix_M = 3; // 固定数组长度时,测试Fix_M个乱序数组
21 const unsigned Length = 6e7; // 固定数组长度
const unsigned Length = 6e7; // 固定数组长度
22 #else
#else
23 const unsigned Fix_M = 10;
const unsigned Fix_M = 10;
24 const unsigned Length = 1e8;
const unsigned Length = 1e8;
25 #endif
#endif
26
27 #if _MSC_VER
#if _MSC_VER
28 #pragma comment(lib, "winmm.lib")
#pragma comment(lib, "winmm.lib")
29 #endif
#endif
30
31
 inline unsigned mclock()
inline unsigned mclock()  { return timeGetTime(); }
{ return timeGetTime(); }
32
33 void solve_1a(const int arr[], const size_t len, int& min_value, int& max_value)
void solve_1a(const int arr[], const size_t len, int& min_value, int& max_value)
34

 {
{
35 min_value = max_value = arr[0];
min_value = max_value = arr[0];
36 for (const int *p = arr + 1; p < arr + len; ++p)
for (const int *p = arr + 1; p < arr + len; ++p)
37 if (*p < min_value) min_value = *p;
if (*p < min_value) min_value = *p;
38 for (const int *p = arr + 1; p < arr + len; ++p)
for (const int *p = arr + 1; p < arr + len; ++p)
39 if (*p > max_value) max_value = *p;
if (*p > max_value) max_value = *p;
40 }
}
41
42
43 void solve_1b(const int arr[], const size_t len, int& min_value, int& max_value)
void solve_1b(const int arr[], const size_t len, int& min_value, int& max_value)
44

 {
{
45 int max_v = arr[0], min_v = arr[0];
int max_v = arr[0], min_v = arr[0];
46 for (const int *p = arr + 1; p < arr + len; ++p)
for (const int *p = arr + 1; p < arr + len; ++p)
47 if (*p < min_v) min_v = *p;
if (*p < min_v) min_v = *p;
48 for (const int *p = arr + 1; p < arr + len; ++p)
for (const int *p = arr + 1; p < arr + len; ++p)
49 if (*p > max_v) max_v = *p;
if (*p > max_v) max_v = *p;
50 max_value = max_v;
max_value = max_v;
51 min_value = min_v;
min_value = min_v;
52 }
}
53
54
55 void solve_2a(const int arr[], const size_t len, int& min_value, int& max_value)
void solve_2a(const int arr[], const size_t len, int& min_value, int& max_value)
56

 {
{
57 int max_v = arr[0], min_v = arr[0];
int max_v = arr[0], min_v = arr[0];
58
 for (const int *p = arr + 1; p < arr + len; ++p)
for (const int *p = arr + 1; p < arr + len; ++p)  {
{
59 if (*p < min_v) min_v = *p;
if (*p < min_v) min_v = *p;
60 if (*p > max_v) max_v = *p;
if (*p > max_v) max_v = *p;
61 }
}
62 max_value = max_v;
max_value = max_v;
63 min_value = min_v;
min_value = min_v;
64 }
}
65
66 void solve_2b(const int arr[], const size_t len, int& min_value, int& max_value)
void solve_2b(const int arr[], const size_t len, int& min_value, int& max_value)
67

 {
{
68 int max_v = arr[0], min_v = arr[0];
int max_v = arr[0], min_v = arr[0];
69
 for (const int *p = arr + 1; p < arr + len; ++p)
for (const int *p = arr + 1; p < arr + len; ++p)  {
{
70 if (*p < min_v) min_v = *p;
if (*p < min_v) min_v = *p;
71 else if (*p > max_v) max_v = *p;
else if (*p > max_v) max_v = *p;
72 }
}
73 max_value = max_v;
max_value = max_v;
74 min_value = min_v;
min_value = min_v;
75 }
}
76
77 void solve_3a(const int arr[], const size_t len, int& min_value, int& max_value)
void solve_3a(const int arr[], const size_t len, int& min_value, int& max_value)
78

 {
{
79 // int min_v = std::numeric_limits<int>::max();
// int min_v = std::numeric_limits<int>::max();
80 // int max_v = std::numeric_limits<int>::min();
// int max_v = std::numeric_limits<int>::min();
81 // const int *low = arr - 1;
// const int *low = arr - 1;
82 // const int *high = arr + len;
// const int *high = arr + len;
83
84 const int *low = arr;
const int *low = arr;
85 const int *high = arr + len - 1;
const int *high = arr + len - 1;
86 int min_v, max_v;
int min_v, max_v;
87
 if (*low < *high)
if (*low < *high)  { min_v = *low; max_v = *high; }
{ min_v = *low; max_v = *high; }
88
 else
else  { min_v = *high; max_v = *low; }
{ min_v = *high; max_v = *low; }
89
90
 while (++low <= --high)
while (++low <= --high)  {
{
91
 if (*low <= *high)
if (*low <= *high)  {
{
92 if (*low < min_v) min_v = *low;
if (*low < min_v) min_v = *low;
93 if (*high > max_v) max_v = *high;
if (*high > max_v) max_v = *high;
94
 } else
} else  {
{
95 if (*high < min_v) min_v = *high;
if (*high < min_v) min_v = *high;
96 if (*low > max_v) max_v = *low;
if (*low > max_v) max_v = *low;
97 }
}
98 }
}
99 max_value = max_v;
max_value = max_v;
100 min_value = min_v;
min_value = min_v;
101 }
}
102
103
104 void solve_3b(const int arr[], const size_t len, int& min_value, int& max_value)
void solve_3b(const int arr[], const size_t len, int& min_value, int& max_value)
105

 {
{
106 // 长度为奇、偶数时,分别先取出1、2个元素。剩下的元素个数一定是偶数
// 长度为奇、偶数时,分别先取出1、2个元素。剩下的元素个数一定是偶数
107 int min_v, max_v;
int min_v, max_v;
108 size_t t = (len - 1u) % 2u;
size_t t = (len - 1u) % 2u;
109
 if (arr[0] <= arr[t])
if (arr[0] <= arr[t])  { min_v = arr[0]; max_v = arr[t]; }
{ min_v = arr[0]; max_v = arr[t]; }
110
 else
else  { min_v = arr[t]; max_v = arr[0]; }
{ min_v = arr[t]; max_v = arr[0]; }
111
112 const int *p = arr + t + 1;
const int *p = arr + t + 1;
113
 while (p < arr + len)
while (p < arr + len)  { // p 和 arr + len 奇偶性始终相同
{ // p 和 arr + len 奇偶性始终相同
114 int va = *p++;
int va = *p++;
115 int vb = *p++;
int vb = *p++;
116
 if (va <= vb)
if (va <= vb)  {
{
117 if (va < min_v) min_v = va;
if (va < min_v) min_v = va;
118 if (vb > max_v) max_v = vb;
if (vb > max_v) max_v = vb;
119
 } else
} else  {
{
120 if (vb < min_v) min_v = vb;
if (vb < min_v) min_v = vb;
121 if (va > max_v) max_v = va;
if (va > max_v) max_v = va;
122 }
}
123 }
}
124
125 max_value = max_v;
max_value = max_v;
126 min_value = min_v;
min_value = min_v;
127 }
}
128
129 void solve_3c(const int arr[], const size_t len, int& min_value, int& max_value)
void solve_3c(const int arr[], const size_t len, int& min_value, int& max_value)
130

 {
{
131 // 长度为奇、偶数时,分别先取出1、2个元素。剩下的元素个数一定是偶数
// 长度为奇、偶数时,分别先取出1、2个元素。剩下的元素个数一定是偶数
132 int min_v, max_v;
int min_v, max_v;
133 size_t t = (len - 1u) % 2u;
size_t t = (len - 1u) % 2u;
134
 if (arr[0] <= arr[t])
if (arr[0] <= arr[t])  { min_v = arr[0]; max_v = arr[t]; }
{ min_v = arr[0]; max_v = arr[t]; }
135
 else
else  { min_v = arr[t]; max_v = arr[0]; }
{ min_v = arr[t]; max_v = arr[0]; }
136
137
138
 for (const int *p = arr + t + 1; p < arr + len; p += 2)
for (const int *p = arr + t + 1; p < arr + len; p += 2)  { // p 和 arr + len 奇偶性始终相同
{ // p 和 arr + len 奇偶性始终相同
139 int va = *p;
int va = *p;
140 int vb = *(p + 1);
int vb = *(p + 1);
141
 if (va <= vb)
if (va <= vb)  {
{
142 if (va < min_v) min_v = va;
if (va < min_v) min_v = va;
143 if (vb > max_v) max_v = vb;
if (vb > max_v) max_v = vb;
144
 } else
} else  {
{
145 if (vb < min_v) min_v = vb;
if (vb < min_v) min_v = vb;
146 if (va > max_v) max_v = va;
if (va > max_v) max_v = va;
147 }
}
148 }
}
149
150 max_value = max_v;
max_value = max_v;
151 min_value = min_v;
min_value = min_v;
152 }
}
153
154
155 static void solve_4a_(const int arr[], size_t low, size_t high, int& min_value, int& max_value)
static void solve_4a_(const int arr[], size_t low, size_t high, int& min_value, int& max_value)
156

 {
{
157
 if (high - low <= 1u)
if (high - low <= 1u)  {
{
158
 if (arr[low] <= arr[high])
if (arr[low] <= arr[high])  { min_value = arr[low]; max_value = arr[high]; }
{ min_value = arr[low]; max_value = arr[high]; }
159
 else
else  { min_value = arr[high]; max_value = arr[low]; }
{ min_value = arr[high]; max_value = arr[low]; }
160 return;
return;
161 }
}
162
163 size_t mid = low + (high - low) / 2u;
size_t mid = low + (high - low) / 2u;
164 int min_left, max_left;
int min_left, max_left;
165 solve_4a_(arr, low, mid, min_left, max_left);
solve_4a_(arr, low, mid, min_left, max_left);
166
167 int min_right, max_right;
int min_right, max_right;
168 solve_4a_(arr, mid + 1, high, min_right, max_right);
solve_4a_(arr, mid + 1, high, min_right, max_right);
169
170 min_value = std::min(min_left, min_right);
min_value = std::min(min_left, min_right);
171 max_value = std::max(max_left, max_right);
max_value = std::max(max_left, max_right);
172 }
}
173
174
175 void solve_4a(const int arr[], const size_t len, int& min_value, int& max_value)
void solve_4a(const int arr[], const size_t len, int& min_value, int& max_value)
176

 {
{
177 return solve_4a_(arr, 0, len - 1u, min_value, max_value);
return solve_4a_(arr, 0, len - 1u, min_value, max_value);
178 }
}
179
180
181
 struct Range
struct Range {
{
182 int min_v, max_v;
int min_v, max_v;
183
 Range(int x, int y):min_v(x), max_v(y)
Range(int x, int y):min_v(x), max_v(y)  {}
{}
184 };
};
185
186
187 static Range solve_4b_(const int arr[], size_t low, size_t high)
static Range solve_4b_(const int arr[], size_t low, size_t high)
188

 {
{
189
 if (high - low <= 1)
if (high - low <= 1)  {
{
190 if (arr[low] <= arr[high]) return Range(arr[low], arr[high]);
if (arr[low] <= arr[high]) return Range(arr[low], arr[high]);
191 return Range(arr[high], arr[low]);
return Range(arr[high], arr[low]);
192 }
}
193 size_t mid = low + (high - low) / 2u;
size_t mid = low + (high - low) / 2u;
194 Range left = solve_4b_(arr, low, mid);
Range left = solve_4b_(arr, low, mid);
195 Range right = solve_4b_(arr, mid + 1, high);
Range right = solve_4b_(arr, mid + 1, high);
196 return Range(std::min(left.min_v, right.min_v),std::max(left.max_v, right.max_v));
return Range(std::min(left.min_v, right.min_v),std::max(left.max_v, right.max_v));
197 }
}
198
199 void solve_4b(const int arr[], const size_t len, int& min_value, int& max_value)
void solve_4b(const int arr[], const size_t len, int& min_value, int& max_value)
200

 {
{
201 Range value = solve_4b_(arr, 0, len - 1);
Range value = solve_4b_(arr, 0, len - 1);
202 min_value = value.min_v;
min_value = value.min_v;
203 max_value = value.max_v;
max_value = value.max_v;
204 }
}
205
206 static void solve_4c_(const int *low, const int *high, int& min_value, int& max_value)
static void solve_4c_(const int *low, const int *high, int& min_value, int& max_value)
207

 {
{
208
 if (high - low <= 1)
if (high - low <= 1)  {
{
209
 if (*low <= *high)
if (*low <= *high)  { min_value = *low; max_value = *high; }
{ min_value = *low; max_value = *high; }
210
 else
else  { min_value = *high; max_value = *low; }
{ min_value = *high; max_value = *low; }
211 return;
return;
212 }
}
213 const int *mid = low + (high - low) / 2u;
const int *mid = low + (high - low) / 2u;
214 int min_left, max_left;
int min_left, max_left;
215 solve_4c_(low, mid, min_left, max_left);
solve_4c_(low, mid, min_left, max_left);
216
217 int min_right, max_right;
int min_right, max_right;
218 solve_4c_(mid + 1, high, min_right, max_right);
solve_4c_(mid + 1, high, min_right, max_right);
219
220 min_value = std::min(min_left, min_right);
min_value = std::min(min_left, min_right);
221 max_value = std::max(max_left, max_right);
max_value = std::max(max_left, max_right);
222 }
}
223
224
225 void solve_4c(const int arr[], const size_t len, int& min_value, int& max_value)
void solve_4c(const int arr[], const size_t len, int& min_value, int& max_value)
226

 {
{
227 return solve_4c_(arr, arr + len - 1, min_value, max_value);
return solve_4c_(arr, arr + len - 1, min_value, max_value);
228 }
}
229
230
231 static Range solve_4d_(const int *low, const int *high)
static Range solve_4d_(const int *low, const int *high)
232

 {
{
233
 if (high - low <= 1)
if (high - low <= 1)  {
{
234 if (*low <= *high) return Range(*low, *high);
if (*low <= *high) return Range(*low, *high);
235 return Range(*high, *low);
return Range(*high, *low);
236 }
}
237 const int* mid = low + (high - low) / 2u;
const int* mid = low + (high - low) / 2u;
238 Range left = solve_4d_(low, mid);
Range left = solve_4d_(low, mid);
239 Range right = solve_4d_(mid + 1, high);
Range right = solve_4d_(mid + 1, high);
240 return Range(std::min(left.min_v, right.min_v),std::max(left.max_v, right.max_v));
return Range(std::min(left.min_v, right.min_v),std::max(left.max_v, right.max_v));
241 }
}
242
243 void solve_4d(const int arr[], const size_t len, int& min_value, int& max_value)
void solve_4d(const int arr[], const size_t len, int& min_value, int& max_value)
244

 {
{
245 Range value = solve_4d_(arr, arr + len - 1);
Range value = solve_4d_(arr, arr + len - 1);
246 min_value = value.min_v;
min_value = value.min_v;
247 max_value = value.max_v;
max_value = value.max_v;
248 }
}
249
250
251
252
253 template<typename T>
template<typename T>
254 void run_test(T arr[], size_t len, int input[], size_t input_len)
void run_test(T arr[], size_t len, int input[], size_t input_len)
255

 {
{
256 int min_value, max_value;
int min_value, max_value;
257
 for (size_t i = 0; i < len; ++i)
for (size_t i = 0; i < len; ++i)  {
{
258 printf("%d %-20s ", i, arr[i].str);
printf("%d %-20s ", i, arr[i].str);
259 unsigned ta = mclock();
unsigned ta = mclock();
260 for (size_t j = Pack; j != 0; --j)
for (size_t j = Pack; j != 0; --j)
261 arr[i].func(input, input_len, min_value, max_value);
arr[i].func(input, input_len, min_value, max_value);
262 ta = mclock() - ta;
ta = mclock() - ta;
263 printf("min/max: %d/%d elapsed: %u ms\n", min_value, max_value, ta / Pack);
printf("min/max: %d/%d elapsed: %u ms\n", min_value, max_value, ta / Pack);
264 }
}
265 printf("\n");
printf("\n");
266 }
}
267
268
 struct Func
struct Func  {
{
269 void (*func)(const int arr[], const size_t len, int& min_value, int& max_value);
void (*func)(const int arr[], const size_t len, int& min_value, int& max_value);
270 const char *str;
const char *str;
271 };
};
272
273
 struct Generator
struct Generator  {
{
274
 int operator()() const
int operator()() const  { return (rand() << 15) + rand(); }
{ return (rand() << 15) + rand(); }
275 };
};
276
277 void test()
void test()
278

 {
{
279 const size_t N = Length;
const size_t N = Length;
280 if (Fix_M == 0 || N < 100) return;
if (Fix_M == 0 || N < 100) return;
281
 const Func func[] =
const Func func[] =  {
{
282

 { solve_1a, " 1a 两次遍历" },
{ solve_1a, " 1a 两次遍历" },
283

 { solve_1b, " 1b 两次遍历(优化)" },
{ solve_1b, " 1b 两次遍历(优化)" },
284

 { solve_2a, " 2a 一次遍历" },
{ solve_2a, " 2a 一次遍历" },
285

 { solve_2b, " 2b 一次遍历(优化)" },
{ solve_2b, " 2b 一次遍历(优化)" },
286

 { solve_3a, " 3a 取头尾两元素" },
{ solve_3a, " 3a 取头尾两元素" },
287

 { solve_3b, " 3b 取相邻两元素" },
{ solve_3b, " 3b 取相邻两元素" },
288 // { solve_3c, " 3c 取相邻两元素2" },
// { solve_3c, " 3c 取相邻两元素2" },
289 #if ! TEST_CASE
#if ! TEST_CASE
290

 { solve_4a, " 4a 分治法" },
{ solve_4a, " 4a 分治法" },
291

 { solve_4b, " 4b 分治法(优化)" },
{ solve_4b, " 4b 分治法(优化)" },
292 // { solve_4c, " 4c 分治法2" }, //
// { solve_4c, " 4c 分治法2" }, //
293 // { solve_4d, " 4d 分治法(优化2)" }, // 用指针,速度会稍快点
// { solve_4d, " 4d 分治法(优化2)" }, // 用指针,速度会稍快点
294 #endif
#endif
295
296 };
};
297
298 const size_t func_len = sizeof(func) / sizeof(func[0]);
const size_t func_len = sizeof(func) / sizeof(func[0]);
299 std::vector<int> src(N);
std::vector<int> src(N);
300 for (size_t i = 0; i < N; ++i) src[i] = i;
for (size_t i = 0; i < N; ++i) src[i] = i;
301
302 #if ! TEST_CASE
#if ! TEST_CASE
303 printf(" 递增 pos: 0 len:%u\n", N);
printf(" 递增 pos: 0 len:%u\n", N);
304 run_test(func, func_len, &src[0], N);
run_test(func, func_len, &src[0], N);
305 for (size_t i = 0; i < N; ++i) src[i] = N - i;
for (size_t i = 0; i < N; ++i) src[i] = N - i;
306 printf(" 递减 pos: 0 len:%u\n", N);
printf(" 递减 pos: 0 len:%u\n", N);
307 run_test(func, func_len, &src[0], N);
run_test(func, func_len, &src[0], N);
308 #endif
#endif
309
310 // srand(time(NULL));
// srand(time(NULL));
311
312
 for (unsigned i = 0; i < Fix_M; ++i)
for (unsigned i = 0; i < Fix_M; ++i)  {
{
313 #if RANDOM_SHUFFLE
#if RANDOM_SHUFFLE
314 std::random_shuffle(src.begin(), src.end());
std::random_shuffle(src.begin(), src.end());
315 #else
#else
316 std::generate(src.begin(), src.end(), Generator());
std::generate(src.begin(), src.end(), Generator());
317 #endif
#endif
318 printf (" 乱序%d pos: 0 len %u\n", i + 1, N);
printf (" 乱序%d pos: 0 len %u\n", i + 1, N);
319 run_test(func, func_len, &src[0], N);
run_test(func, func_len, &src[0], N);
320 }
}
321
322 #if TEST_RAND_POS
#if TEST_RAND_POS
323 const unsigned sub_len = N / 4u;
const unsigned sub_len = N / 4u;
324 const unsigned max_pos = N - sub_len;
const unsigned max_pos = N - sub_len;
325
 for (unsigned i = 0; i < Rand_M; ++i)
for (unsigned i = 0; i < Rand_M; ++i)  {
{
326 size_t pos = rand() % max_pos;
size_t pos = rand() % max_pos;
327 printf (" 乱序 pos: %u len %u\n", pos, sub_len);
printf (" 乱序 pos: %u len %u\n", pos, sub_len);
328 run_test(func, func_len, &src[pos], sub_len);
run_test(func, func_len, &src[pos], sub_len);
329 }
}
330 #endif
#endif
331
332 }
}
333
334
335 int main()
int main()
336

 {
{
337 const HANDLE handle = GetCurrentProcess();
const HANDLE handle = GetCurrentProcess();
338 SetPriorityClass(handle, REALTIME_PRIORITY_CLASS);
SetPriorityClass(handle, REALTIME_PRIORITY_CLASS);
339 SYSTEM_INFO info;
SYSTEM_INFO info;
340 GetSystemInfo(&info);
GetSystemInfo(&info);
341 const int num = info.dwNumberOfProcessors;
const int num = info.dwNumberOfProcessors;
342 if (num > 1) SetProcessAffinityMask(handle, num);
if (num > 1) SetProcessAffinityMask(handle, num);
343 test();
test();
344 }
}
345
346