《数据结构》这门课是计算机专业的核心课程,但往往却让人头痛,因为比较抽象,当然了,也许你足够聪明,并不觉得它有多难,但对我而言,是有点难度,后来我仔细想了想,到底哪里难?我得出这么个结论:长篇大论,缺乏图表。现在的人都喜欢看电影,看电视剧,很少人还热衷于看小说吧,密密麻麻的文字不如一些图来得直观。
另外,我们大多数人是做应用的,不是做研究的,所以我们只需要知道2+3=5,而不需要知道a+b=c。所以我就不深入理论,再说自己也没那个能力。
好,接下去我就用最一般的例子,最通俗易懂的图,算法和尽量少的文字,描述某作者需要长篇大论方可完成教材。
一、大圈表示法
面试时候如果让你写一个算法,要求复杂度为Ο(n),你明白是什么意思吗?说起数据结构,就先提一下这个表示法吧,后面会用到。
“Ο”,其实不是英文的“O”,它是个希腊字母,发音大概是“欧麦克隆”,所以我们一般说“圈”而不是跟英文的O一样的发音。简单地说,大圈表示法是一种用于表示算法复杂度数量级的方法。要精确描述这个表示法,很难,不过我们不需要懂那么精确,只要八九不离十就可以了。下面我列个表,复杂度从低到高,大家就知道其意义:
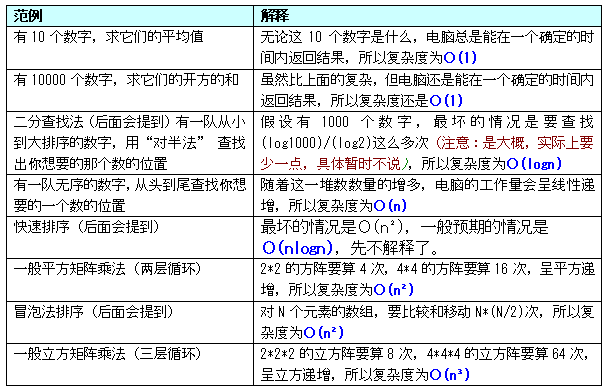
另外还有个叫指数复杂度,这里不提,因为见得实在太少,“指数级递增”本身就是一个很夸张的形容词,我们也要避免这种复杂度的出现。还需要说明的一点是大圈表示法是时间递增数量级的表示方法,注意“递增”两个字,所以并不是说复杂度为Ο(1)的算法消耗的时间一定比复杂度为Ο(n)的算法少。
如果你还是不太明白大圈表示法,不用担心,继续往下看,会慢慢明白的。
二、动态数组(Dynamic Array)
接下去介绍最最基本的两种数据结构,即动态数组和单向链表,其它数据结构其实都可以通过这两者衍生出来。BTW:如果算法太简单,我就不列出代码,只稍微描述一下。

这就是一个最基本的动态数组,pData记录了数组第一个元素的位置,Unit Size记录了每个元素的大小,(这样可以方便地找到第N个元素了)Unit Number记录了元素的数目。
获取数组中第N个元素,是很简单的,无需多说。
但已知某位置,要插入一个元素,就稍微有点难,因为要挪动一些元素,如图:
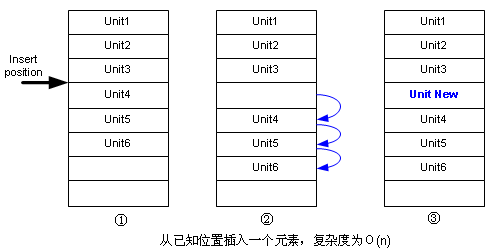
删除元素跟这个也类似,也是需要挪一挪后面的元素,只不过是往前挪。
数组的大小不能很方便地调整,需要几个步骤,如下图所示:
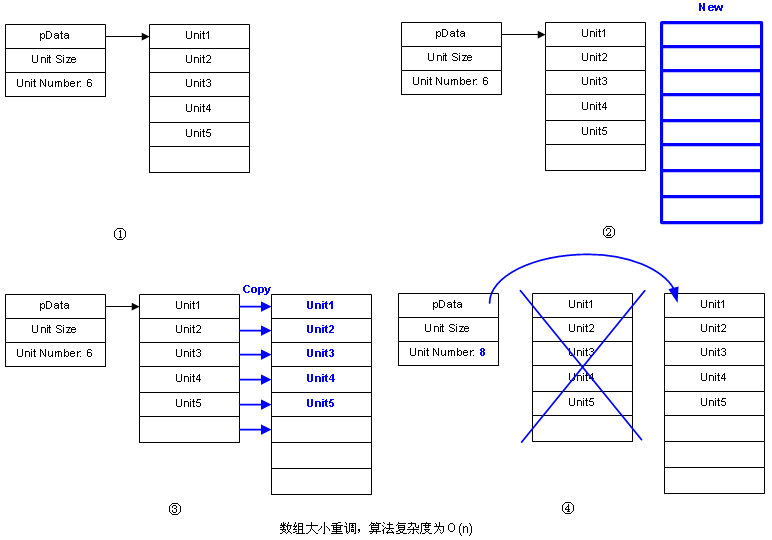
代码我就不写了,大概就是new,memcpy,delete这几个步骤。
三、单向链表(Singly-linked List)
下图就是最简单最一般的单向链表:

还有这种:

多一个Tail指针,好处就是能很方便地找到末尾,然后在末尾插入新的元素什么的。还有这种也比较常见:
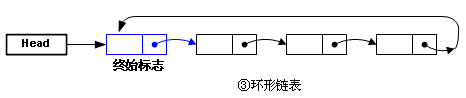
留一个终始标志,这个节点作为一个标志,不用于存储数据,链表末尾指向这个节点,形成一个“环形链表”,这样无论在链表的哪里插入新的元素,操作都一致了,不必判断头和尾的特殊性。
数组的好处就是链表的坏处,数组的坏处就是链表的好处,请看:

因为需要从头开始找,没办法像数组那样直接跳到那个地址。而插入元素,就比数组方便了,如果你已经得知了要插入的地址的话,不过还要注意哦,是“后插入”(Insert After):
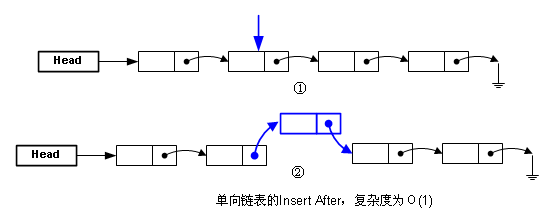
有“后插入”,那就有“前插入”(Insert Before),两者对单向链表来说真的不一样,下图描述了“前插入”:
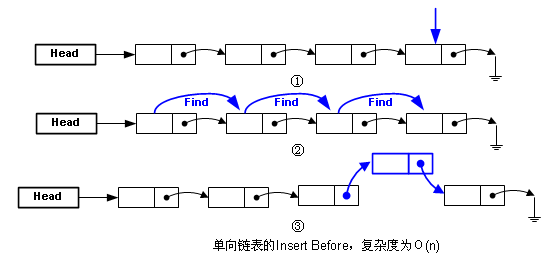
由于指针向后不向前,我们不知道要插入位置的前一个节点是什么,只能从头找,所以比较麻烦。
至于链表大小的重新调整,和数组相比如何呢?呃……我可没说链表有大小限制吧?
(未完待续……)