四、栈(Stack)
前一篇讲解了最基本的东西,这篇就稍微前进一点点,讲一下栈,栈在英文中叫Stack,翻译成中文又叫“堆栈”,但决不能称为“堆”,这个要搞清楚,我们说的“栈”和“堆栈”指的都是Stack这种数据结构,但“堆”却是另外一个概念了,这里且不提。
栈最大特点是先进后出,如图:
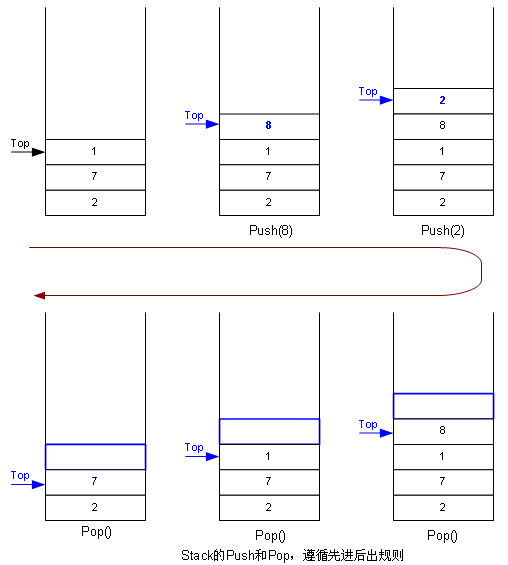
可以看出,栈有几个最常见的方法,或者说必备的方法,Push,Pop和Top,即进栈,出栈和取最顶元素。从代码上看,栈如何实现呢?用数组好还是用单向链表好呢?其实都可以,我下面的例子是用数组实现的。
说了那么多,栈有什么用呢?下面就举一个最经典的例题——逆波兰表达式(RPN,Reversed Polish Notation)的求解。
什么是逆波兰表达式?我们表述一个算式通常是这样:X+Y,即:“操作数1 操作符 操作数2”,当然也有比较特别的,比如“sqrt(N)”,sqrt是操作符,N是操作数,而逆波兰表达式则很统一,先操作数,后操作符,为什么叫“逆波兰表达式”?因为有一个波兰人发明了波兰表达式,而逆的波兰表达式就叫“逆波兰表达式”了。看下图就能很好理解了:

所有的算式都可以用逆波兰表达式写出来,只是我这里的举例是为了方便起见,限制在整数的四则运算里。
那假如现在我们有一个逆波兰表达式,那我们如何求出它的值呢?这里我们的“栈”就要派上用场了,由于操作数在操作符前面,所以我们按顺序遍历这个表达式,遇到操作数的时候进栈,遇到操作符时候让操作数出栈并运算,然后把运算结果进栈。过程如下图所示:
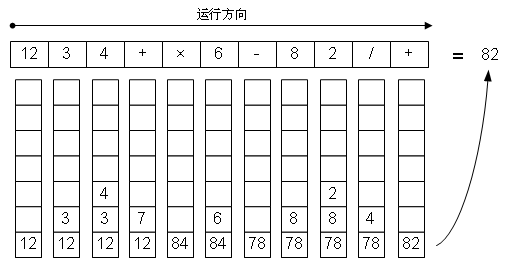
遇到第一个操作符,“+”的时候,由于需要两个操作数,所以出栈两次,4和3出栈,执行加法运算,结果是7,7进栈……依此类推。
下面我给出参考代码,我的代码使用很简单,复制,粘贴到一个cpp文件中,编译此cpp文件即可,没别的依赖。
#include "stdio.h"
struct Cell
{
int iType; // 0 - number, 1 - '+', 2 - '-', 3 - '*', 4 - '/'
int iData;
};
class Stack
{
public:
Stack(int iAmount = 10);
~Stack();
//return 1 means succeeded, 0 means failed.
int Pop(int& iVal);
int Push(int iVal);
int Top(int& iVal);
private:
int *m_pData;
int m_iCount;
int m_iAmount;
};
Stack::Stack(int iAmount)
{
m_pData = new int[iAmount];
m_iCount = 0;
m_iAmount = iAmount;
}
Stack::~Stack()
{
delete m_pData;
}
int Stack::Pop(int& iVal)
{
if(m_iCount>0)
{
--m_iCount;
iVal = m_pData[m_iCount];
return 1;
}
return 0;
}
int Stack::Push(int iVal)
{
if(m_iCount<m_iAmount)
{
m_pData[m_iCount] = iVal;
++m_iCount;
return 1;
}
return 0;
}
int Stack::Top(int& iVal)
{
if(m_iCount>0 && m_iCount<=m_iAmount)
{
iVal = m_pData[m_iCount-1];
return 1;
}
return 0;
}
int main(int argc, char* argv[])
{
//12 3 4 + * 6 - 8 2 / +
Cell rpn[11] = {
0, 12,
0, 3,
0, 4,
1, 0,
3, 0,
0, 6,
2, 0,
0, 8,
0, 2,
4, 0,
1, 0};
Stack st;
// I won't check the return value for this is just a demo.
int i, iOpt1, iOpt2;
for(i=0; i<sizeof(rpn)/sizeof(Cell); i++)
{
switch(rpn[i].iType)
{
case 0: // number
st.Push(rpn[i].iData);
break;
case 1: // +
st.Pop(iOpt2);
st.Pop(iOpt1);
st.Push(iOpt1 + iOpt2);
break;
case 2: // -
st.Pop(iOpt2);
st.Pop(iOpt1);
st.Push(iOpt1 - iOpt2);
break;
case 3: // *
st.Pop(iOpt2);
st.Pop(iOpt1);
st.Push(iOpt1 * iOpt2);
break;
case 4: // /
st.Pop(iOpt2);
st.Pop(iOpt1);
st.Push(iOpt1 / iOpt2);
break;
}
}
int iResult;
st.Pop(iResult);
printf("The result is %d\n", iResult);
return 0;
}
(未完待续……)