十三、左偏树(Leftist Tree)
树这个数据结构内容真的很多,上一节所讲的二叉堆,其实就是一颗二叉树,这次讲的左偏树(又叫“左翼堆”),也是树。
二叉堆是个很不错的数据结构,因为它非常便于理解,而且仅仅用了一个数组,不会造成额外空间的浪费,但它有个缺点,那就是很难合并两个二叉堆,对于“合并”,“拆分”这种操作,我觉得最方面的还是依靠指针,改变一下指针的值就可以实现,要是涉及到元素的移动,那就复杂一些了。
左偏树跟二叉堆比起来,就是一棵真正意义上的树了,具有左右指针,所以空间开销上稍微大一点,但却带来了便于合并的便利。BTW:写了很多很多的程序之后,我发觉“空间换时间”始终是个应该考虑的编程方法。:)
左偏左偏,给人感觉就是左子树的比重比较大了,事实上也差不多,可以这么理解:左边分量重,那一直往右,就一定能最快地找到可以插入元素的节点了。所以可以这样下个定义:左偏树就是对其任意子树而言,往右到插入点的距离(下面简称为“距离”)始终小于等于往左到插入点的距离,当然了,和二叉堆一样,父节点的值要小于左右子节点的值。
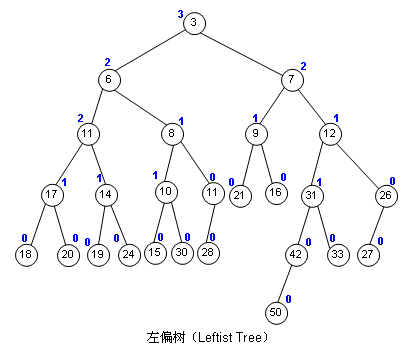
如果节点本身不满,可插入,那距离就为0,再把空节点的距离记为-1,这样我们就得出:父节点的距离 = 右子节点距离 + 1,因为右子节点的距离始终是小于等于左子节点距离的。我把距离的值用蓝色字体标在上图中了。
左偏树并一定平衡,甚至它可以很不平衡,因为它其实也不需要平衡,它只需要像二叉堆那样的功能,再加上合并方便,现在来看左偏树的合并算法,如图:
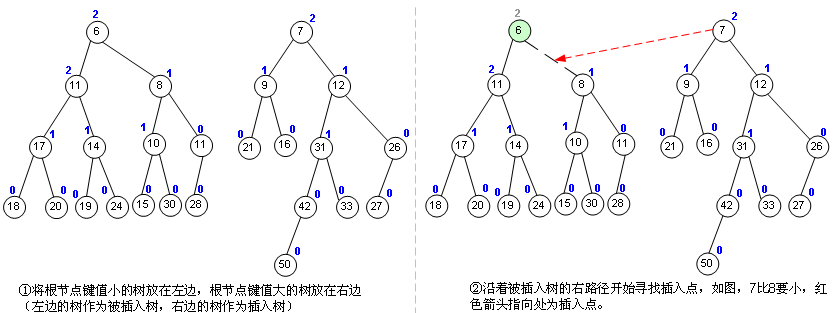
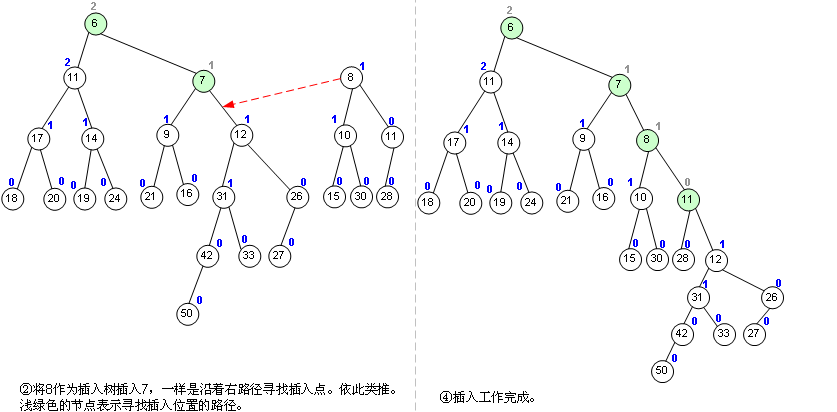
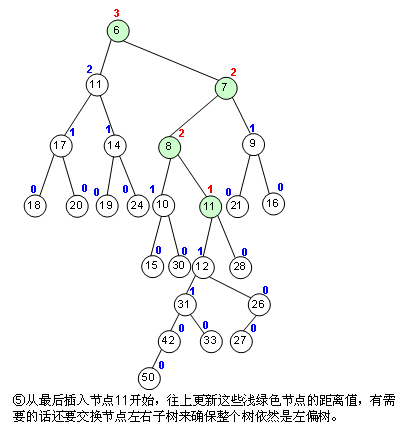
这种算法其实很适合用递归来做,但我还是用了一个循环,其实也差不多。对于左偏树来说,这个合并操作是最重要最基本的了。为什么?你看哦:Enqueue,我能不能看作是这个左偏树的root和一个单节点树的合并?而Dequeue,我能不能看作是把root节点取出来,然后合并root的左右子树?事实上就是这样的,我提供的代码就是这样干的。
Conclusion:左偏树比同二叉堆的优点就是方便合并,缺点是编程复杂度略高(也高不去哪),占用空间稍大(其实也大不去哪)。附上代码,老样子了,单个文件,直接调试的代码,零依赖零配置,一看就懂,代码虽然不算完美,但作为演示和学习,是足够了。
#include <stdio.h>
// TreeNode
//////////////////////////////////////////////////////////////////////////
struct TreeNode
{
TreeNode(int iVal)
{
m_iData = iVal;
m_iDistance = 0;
m_pLeft = 0;
m_pRight = 0;
}
~TreeNode()
{
}
void SwapLeftRight()
{
TreeNode *pTmp = m_pLeft;
m_pLeft = m_pRight;
m_pRight = pTmp;
}
void UpdateDistance()
{
m_iDistance = GetRightDistance()+1;
}
int GetLeftDistance()
{
return m_pLeft!=0?m_pLeft->m_iDistance:-1;
}
int GetRightDistance()
{
return m_pRight!=0?m_pRight->m_iDistance:-1;
}
int m_iData;
int m_iDistance;
TreeNode* m_pLeft;
TreeNode* m_pRight;
};
// Stack
//////////////////////////////////////////////////////////////////////////
class Stack
{
public:
Stack(int iAmount = 10);
~Stack();
//return 1 means succeeded, 0 means failed.
int Pop(TreeNode* & val);
int Push(TreeNode* val);
int Top(TreeNode* & val);
//iterator
int GetTop(TreeNode* &val);
int GetNext(TreeNode* &val);
private:
TreeNode** m_pData;
int m_iCount;
int m_iAmount;
//iterator
int m_iCurr;
};
Stack::Stack(int iAmount)
{
m_pData = new TreeNode*[iAmount];
m_iCount = 0;
m_iAmount = iAmount;
m_iCurr = 0;
}
Stack::~Stack()
{
delete m_pData;
}
int Stack::Pop(TreeNode* & val)
{
if(m_iCount>0)
{
--m_iCount;
val = m_pData[m_iCount];
return 1;
}
return 0;
}
int Stack::Push(TreeNode* val)
{
if(m_iCount<m_iAmount)
{
m_pData[m_iCount] = val;
++m_iCount;
return 1;
}
return 0;
}
int Stack::Top(TreeNode* & val)
{
if(m_iCount>0 && m_iCount<=m_iAmount)
{
val = m_pData[m_iCount-1];
return 1;
}
return 0;
}
int Stack::GetTop(TreeNode* &val)
{
if(m_iCount>0 && m_iCount<=m_iAmount)
{
val = m_pData[m_iCount-1];
m_iCurr = m_iCount - 1;
return 1;
}
return 0;
}
int Stack::GetNext(TreeNode* &val)
{
if((m_iCurr-1)<(m_iCount-1) && (m_iCurr-1)>=0)
{
--m_iCurr;
val = m_pData[m_iCurr];
return 1;
}
return 0;
}
// LeftistTree
//////////////////////////////////////////////////////////////////////////
class LeftistTree
{
public:
LeftistTree();
~LeftistTree();
//return 0 means failed.
int Dequeue(int& iVal);
int Enqueue(int iVal);
//returns the merged root.
TreeNode* Merge(TreeNode *pT1, TreeNode *pT2);
TreeNode* GetRoot();
#ifdef _DEBUG
void Print(TreeNode* pNode);
#endif
protected:
TreeNode *m_pRoot;
};
LeftistTree::LeftistTree()
{
m_pRoot = NULL;
}
LeftistTree::~LeftistTree()
{
Stack st(40); //2^40 must be enough.
//Postorder traverse the tree to release all nodes.
TreeNode *pNode = m_pRoot;
TreeNode *pTemp;
if(pNode==0)
return;
while (1)
{
if(pNode->m_pLeft!=0)
{
st.Push(pNode);
pTemp = pNode;
pNode = pNode->m_pLeft;
pTemp->m_pLeft = 0;
continue;
}
if(pNode->m_pRight!=0)
{
st.Push(pNode);
pTemp = pNode;
pNode = pNode->m_pRight;
pTemp->m_pRight = 0;
continue;
}
delete pNode;
if(0==st.Pop(pNode))
break;
}
}
int LeftistTree::Dequeue(int& iVal)
{
if(m_pRoot==0)
return 0;
iVal = m_pRoot->m_iData;
TreeNode *pTmp = m_pRoot;
m_pRoot = Merge(m_pRoot->m_pLeft, m_pRoot->m_pRight);
delete pTmp;
return 1;
}
int LeftistTree::Enqueue(int iVal)
{
TreeNode *pNew = new TreeNode(iVal);
m_pRoot = Merge(m_pRoot, pNew);
return 1;
}
TreeNode* LeftistTree::Merge(TreeNode *pT1, TreeNode *pT2)
{
if(pT1==0 && pT2==0)
return 0;
else if(pT1==0) //pT2!=0
return pT2;
else if(pT2==0) //pT1!=0
return pT1;
if(pT1->m_iData > pT2->m_iData)
return Merge(pT2, pT1);
Stack st(40);
TreeNode* pInsPos = pT1;
TreeNode* pToIns = pT2;
TreeNode* pTmp;
st.Push(pInsPos);
//Find a node available for insert.
while(1)
{
if(pInsPos->m_pRight!=NULL)
{
if(pToIns->m_iData < pInsPos->m_pRight->m_iData)
{
pTmp = pInsPos->m_pRight;
pInsPos->m_pRight = pToIns;
pToIns = pTmp;
st.Push(pInsPos);
pInsPos = pInsPos->m_pRight;
}
else
{
st.Push(pInsPos);
pInsPos = pInsPos->m_pRight;
}
}
else
{
st.Push(pInsPos);
//Insert
pInsPos->m_pRight = pToIns;
break;
}
}
TreeNode* pNode;
//Try to update the relative distance and make the tree be still the leftist tree.
while (0!=st.Pop(pNode))
{
if(pNode->GetLeftDistance() < pNode->GetRightDistance())
pNode->SwapLeftRight();
pNode->UpdateDistance();
}
return pT1;
}
TreeNode* LeftistTree::GetRoot()
{
return m_pRoot;
}
#ifdef _DEBUG
void LeftistTree::Print(TreeNode* pNode)
{
if(pNode!=NULL)
{
if(pNode->m_pLeft!=NULL && pNode->m_pRight!=NULL)
{
printf("%d[%d]->(%d, %d)\n", pNode->m_iData, pNode->m_iDistance, pNode->m_pLeft->m_iData, pNode->m_pRight->m_iData);
Print(pNode->m_pLeft);
Print(pNode->m_pRight);
}
else if(pNode->m_pLeft!=NULL)
{
printf("%d[%d]->(%d, x)\n", pNode->m_iData, pNode->m_iDistance, pNode->m_pLeft->m_iData);
Print(pNode->m_pLeft);
}
else if(pNode->m_pRight!=NULL)
{
printf("%d[%d]->(x, %d)\n", pNode->m_iData, pNode->m_iDistance, pNode->m_pRight->m_iData);
Print(pNode->m_pRight);
}
}
}
#endif
int main(int argc, char* argv[])
{
LeftistTree tree;
tree.Enqueue(9);
tree.Enqueue(4);
tree.Enqueue(2);
tree.Enqueue(1);
tree.Enqueue(3);
tree.Enqueue(8);
#ifdef _DEBUG
tree.Print(tree.GetRoot());
#endif
int iVal;
tree.Dequeue(iVal);
printf("\nDequeue value is %d\n", iVal);
tree.Dequeue(iVal);
printf("Dequeue value is %d\n", iVal);
#ifdef _DEBUG
tree.Print(tree.GetRoot());
#endif
return 0;
}
也许你还想问:怎么你写的代码都不加个头啊,用来声明版权什么的。本人似乎没这个习惯,那些东西繁琐得很,而且根据我多年开发经验,给每个cpp文件加个头其实是没有必要的,就好像注释,不需要的时候也生硬加上,那就是画蛇添足了。
(未完待续)