递归通常很直白地描述了一个求解过程,因此也是最容易被想到和实现的算法。循环其实和递归具有相同的特性(即:做重复任务),但有时,使用循环的算法并不会那么清晰地描述解决问题步骤。单从算法设计上看,递归和循环并无优劣之别。然而,在实际开发中,因为函数调用的开销,递归常常会带来性能问题,特别是在求解规模不确定的情况下。而循环因为没有函数调用开销,所以效率会比递归高。除少数编程语言对递归进行了优化外,大部分语言在实现递归算法时还是十分笨拙,由此带来了如何将递归算法转换为循环算法的问题。算法转换应当建立在对求解过程充分理解的基础上,有时甚至需要另辟蹊径。
前段时间遇到过这样的问题:已知一2D地图格子的长宽(w、h)及每个格子的边长(a,格子为正方形),给定物体的2D坐标(pos[x , y])及半径(r),求解物体在2D地图格子中所占的格子,仅考虑n*n的情况。大概的求解过程如下:
1)根据半径,确定n*n中的n。假定计算公式为:n = Round(2*r / a)
2)根据2D坐标得到物体的“中心格子”。根据n的奇偶,计算公式不同,如下图所示。
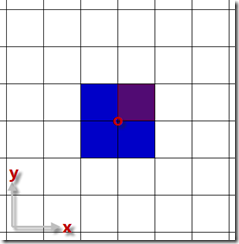
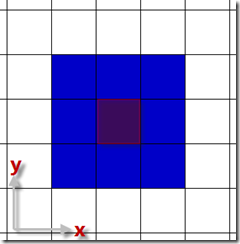
n为偶数[1] n为奇数[2]
[1]:grid(x , y) = Round(pos / a)
[2]:grid(x , y) = Floor(pos / a)
其中,格子坐标x >= 0 , y >= 0。
3)以“中心格子”为基础,求出物体占据的其他格子。这样的描述,让人容易想到递归,就像用深度优先方法遍历树那样,伪代码算法如下:
if n is even
{
get the index of 'center grid' (row , col)
ExtendHeldGrid(row , col , n)
ExtendHeldGrid(row - 1 , col , n)
ExtendHeldGrid(row - 1 , col - 1 , n)
ExtendHeldGrid(row , col - 1 , n)
}
else
{
get the index of 'center grid' (row , col)
ExtendHeldGrid(row , col , n)
}
function ExtendHeldGrid(row , col , level)
{
if(level <= 0)
return
if((row >= 0 and row < MaxGridWidth) and (col >= 0 and col < MaxGridHeight))
{
mark the grid(row , col)
ExtendHeldGrid(row , col , level - 2)
if(level - 2 > 0)
{
ExtendHeldGrid(row + 1 , col , level - 2)
ExtendHeldGrid(row - 1 , col , level - 2)
ExtendHeldGrid(row , col + 1 , level - 2)
ExtendHeldGrid(row , col - 1 , level - 2)
ExtendHeldGrid(row + 1 , col + 1 , level - 2)
ExtendHeldGrid(row - 1 , col + 1 , level - 2)
ExtendHeldGrid(row + 1 , col - 1 , level - 2)
ExtendHeldGrid(row - 1 , col - 1 , level - 2)
}
}
}
虽然,该算法得到了正确的求解结果,但是由于每个格子都会标记周围的8个格子,所以存在大量的重复,再者如果上面的过程每帧都进行的话,函数调用开销也是相当可观。
循环自然是不可避免的,消除重复便成了优化的目标。分析格子图和n为2和3的情况,试图找出用循环代替递归的方法,我发现了下面一个有趣的规律:
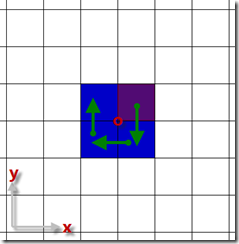
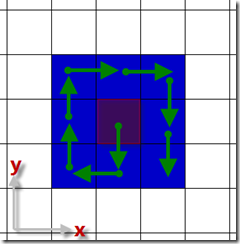
从“中心格子”出发,顺时针(或逆时针)以上图方式可以走遍所求解的每个格子而不重复。在实现上,每个转角也是有规律的,可以通过一个2*2的转角矩阵来控制:
[1 , 0][0 , -1]
[0 , 1][-1 , 0]
顺时针方式的转角阵
矩阵中的每个元素代表从当前格子走到下个格子在row和col上的变化。加之,在转角之间的路长(以格子个数计)有每转两次递增单位1的规律,算法就不难得到了,下面同样以伪代码示:
conerMat =
{
{0 , -1} ,
{-1 , 0} ,
{0 , 1} ,
{1 , 0}
}
dir = 0 /// 转角控制,四个转角顺时针0~3
span = 1 /// 转角间的跨度
count = 1 /// 每两次增加一个跨度
rin = 1 /// 下一个转角的循环索引
if n is even
get the index of 'center grid' (row , col)
else
get the index of 'center grid' (row , col)
for(i = 0; i < n * n; ++i)
{
if((row >= 0 and row < MaxGridWidth) and (col >= 0 and col < MaxGridHeight))
mark the grid(row , col)
if(i == rin)
{
dir = (dir + 1) % 4
if(count == 2)
{
++span
count = 1
}
else
++count
rin = i + span
}
row = row + conerMat[dir][0]
col = col + conerMat[dir][1]
}
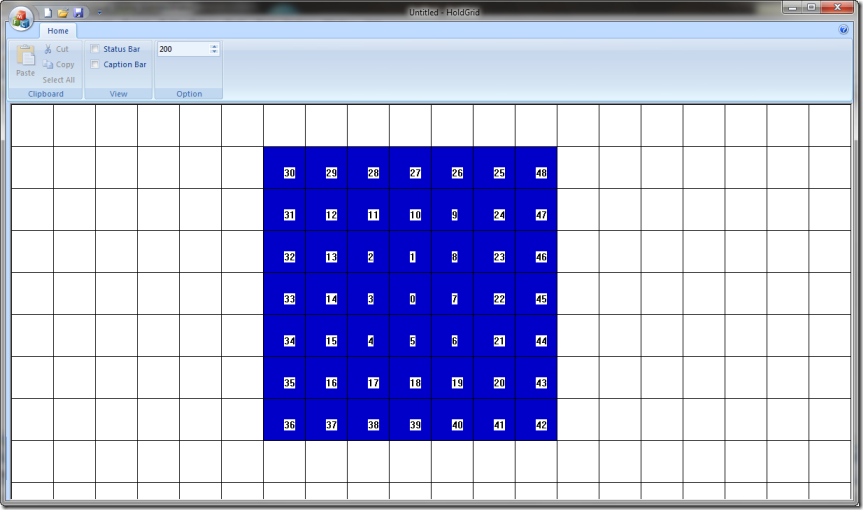
用MFC程序验证了一下算法的正确性,标号展示了循环的路线(注意GDI的坐标系中Y的正方向朝下):