转自:http://blog.csdn.net/pennyliang/archive/2010/07/07/5717498.aspx
中文分词方法有很多,其中基于词典的分词方法有:
正向最大匹配、逆向最大匹配法、双向匹配法
最少分词法
基于统计的分词方法有:
- 统计语言模型分词(2-gram,3-gram)
- 串频统计的汉语自动分词
除了这些基本的方法,为了获得最佳的效果,也可以引入动态规划的方法获得最优解。
设句子P = W0W1W2⋯Wn , 其中Wi (0≤i≤n) 为句子P中的第i 个汉字。Si(0≤i≤n+1)为句子的第i个间隙(切分位置)
那么一个句子P理论上有多少种分词法呢?
分词分法总数的通项:F(n)表示一个有n个单词的句子包含的全部不同的分词方法。
F(n)=1+ F(n-1)+F(n-2)+F(n-3)+F(n-4)+..F(1)
F(1)=1
F(2)=2
F(3)=4
F(4)=8
…
F(n)=2F(n-1)
则F(n)=2n-1
如果将词频看做是距离,则求解最佳切分方法等价于在2n-1的解空间中寻找1种最佳的切分方法使得路径最短。为此我们举个例子:
早起先刷牙
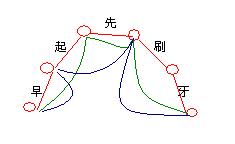
图中红圈为切分点,切分点之间的连线表示确定的一种分词
图中给出了三种分法,分别是[早][起][先][刷][牙]、[早起][先][刷牙]和[早][起先][刷牙]
假定我们有这样一个字频和词频表,分别如下
早 400
早起 100
起 500
起先 150
先 500
刷 300
刷牙 100
牙 500
则以上三种切分法的代价分别为
[早][起][先][刷][牙]:400+500+500+300+500 = 2200
[早起][先][刷牙]:100+500+100 = 700
[早][起先][刷牙]:400+150+100 =750 (此处应为650)
因此选用第2种切分法。
动态规划的伪代码大致为:
Segment(S,low,high,cost,last)
{
Mincost = MAX;
If(high-low<=1)
{
mincost = Costof(cost,L(low,high-low)); //其中L(start,length)的含义表示从start开始从P中取length长度的文本,Costof为该段文本的字频,或者词频,如果不存在则为无穷大;如果cost数组中已经计算过,则不重复计算,直接取值返回。
cost[low][high] = mincost;
Return mincost;
}
for(i = low+1 to high )
{
a = Segment(S,low,i,cost,last);//为了简单这里做了精简,事实上如果a返回的是无穷大,则后面不用继续计算,直接跳出,因为这种情况下无论如何也不可能是最优解,可以直接剪枝。
b = Segment(S,i,high,cost,last);
if(a+b<Mincost)
{
Mincost = a + b;
Cost[low][high]=Mincost;
Last[low][high] = i;//Last记录最佳切分点
}
}
ExtractSegmentPos(Last,low,high);//该函数是将切分点一一展开。
}
ExtractSegmentPos(Last,low,high)
{
SegPos=MAX;
if(high-low>1)
{
If(Last[low][high]>0)
{
SegPos = Last[low][high];
output(SegPos);
}
else
{
return;
}
}
ExtractSegmentPos(Last,low, SegPos);
ExtractSegmentPos(Last, SegPos,high);
}
参考文献
[1] 孙 晓, 黄德根 基于动态规划的最小代价路径汉语自动分词 [J]小型微型计算机系统 第27 卷第3 期 2006 年3 月
其他推荐阅读
http://www.leadbbs.com/MINI/default.asp?230-2682632-0-0-0-0-0-a-.htm
posted on 2010-07-30 09:06
胡满超 阅读(789)
评论(0) 编辑 收藏 引用