网上搜了下棋盘覆盖，结果看到了哈佛校训。。。。
棋盘覆盖是在一个2^k*2^k的棋盘中存在一个特殊格子，现要求用L型覆盖整个棋盘（除特殊格子），问如何覆盖这个棋盘？
在学校的时候，这题目是只看懂了解题思路，代码没仔细看过，现在在重新看的时候，感觉其实也不是那么难看懂！
先看解题思路截图：
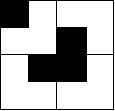
看到这个截图你会有何感想呢？其实不就是个分治嘛！将一个2^k*2^k棋盘分割成4个2^(k-1)*2^(k-1),然后问题回到原点，在2^(k-1)*2^(k-1)棋盘中有一个特殊格子，求其用L型骨牌覆盖方法！
代码如下：
#include<stdio.h>
int Board[64][64];
int tile;
void ChessBoard(int tr,int tc,int dr,int dc,int size)//tr为棋盘左上角方格行号，tc为棋盘左上角列号，dr为特殊格行号，dc为特殊格列号，size=2^k，棋盘规格
{
if(size==1) //当分到只剩下一个格子的时候,该格就是本次递归特殊格
return ;
int t=++tile;
int s=size/2;
if(dr<tr+s&&dc<tc+s) //特殊格在棋盘左上角
ChessBoard(tr,tc,dr,dc,s);
else
{
Board[tr+s-1][tc+s-1]=t;
ChessBoard(tr,tc,tr+s-1,tc+s-1,s);
}
if(dr<tr+s&&dc>=tc+s) //特殊格在棋盘右上角
ChessBoard(tr,tc+s,dr,dc,s);
else
{
Board[tr+s-1][tc+s]=t;
ChessBoard(tr,tc+s,tc+s-1,tc+s,s);
}
if(dr>=tr+s&&dc<tc+s) //特殊格在棋盘左下角
ChessBoard(tr+s,tc,dr,dc,s);
else
{
Board[tr+s][tc+s-1]=t;
ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
}
if(dr>=tr+s&&dc>=tc+s) //特殊格在棋盘右下角
ChessBoard(tr+s,tc+s,dr,dc,s);
else
{
Board[tr+s][tc+s]=t;
ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
}
}
int main()
{
int i,j,k,l;
/**//*for(k=0;k<64;k++)
for(l=0;l<64;l++)
{ */
Board[2][1]=0;
tile=0;
ChessBoard(0,0,2,1,4);
for(i=0;i<4;i++)
{
for(j=0;j<4;j++)
{
printf("%d ",Board[i][j]);
}
printf("\n");
}
printf("\n");
// }
return 0;
}输出结果：
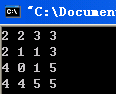
哈佛校训：
此刻打盹，你将做梦，此刻学习，你将圆梦！ 受教！！
posted on 2010-09-02 13:59
jince 阅读(430)
评论(0) 编辑 收藏 引用 所属分类:
算法设计与分析