问题描述：给定序列X={x1,x2,..xn}和Y={y1,y2...ym},求一个Z={z1,z2,..zk}序列是X,Y的最长公共子序列！！
书上描述的已经十分详细了，而且容易理解。通过定义c[i][j]用于记录Xi和Yi的最长公共子序列的长度，从而递推得到结果。
递推方程如下：
c[i][j]=0,i=0,j=0； c[i][j]=c[i-1][j-1]+1,xi=yj； c[i][j]=max(c[i-1][j],c[i][j-1]),xi!=yj；
（不知道怎么输出大括号，悲剧啊！）
代码如下：
#include<stdio.h>
void LCSLength(int m,int n,char *x,char *y,int c[][100],int b[][100])
{
int i,j;
for(i=1;i<=m;i++) c[i][0]=0; //当i==0或者j==0时，代表其中一个序列为空，c[i][j]当然为0
for(j=1;j<=n;j++) c[0][j]=0;
for(i=1;i<=m;i++) //二重循环
for(j=1;j<=n;j++)
{
if(x[i]==y[j])
{
c[i][j]=c[i-1][j-1]+1;
b[i][j]=1;
}
else
{
if(c[i-1][j]>=c[i][j-1])
{
c[i][j]=c[i-1][j];
b[i][j]=2;
}
else
{
c[i][j]=c[i][j-1];
b[i][j]=3;
}
}
}
}
void LCS(int i,int j,char x[],int b[][100]) //递归求得最长子序列
{
if(i==0||b==0)
return;
if(b[i][j]==1)
{
LCS(i-1,j-1,x,b);
printf("%c",x[i]);
}
else if(b[i][j]==2)
LCS(i-1,j,x,b);
else
LCS(i,j-1,x,b);
}
int main()
{
char x[100],y[100];
int i,j;
int c[100][100],b[100][100];
scanf("%s %s",x+1,y+1);
c[0][0]=0;
LCSLength(7,6,x,y,c,b);
for(i=0;i<8;i++)
{
for(j=0;j<7;j++)
{
printf("%d ",c[i][j]);
}
printf("\n");
}
LCS(7,6,x,b);
printf("\n");
return 0;
}
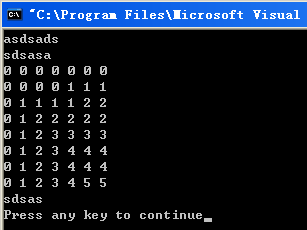
运行结果：
posted on 2010-09-04 23:17
jince 阅读(320)
评论(0) 编辑 收藏 引用 所属分类:
算法设计与分析