问题描述:在一块电路板的上、下两端分别有n个接线柱。根据电路设计,要求用导线(i,π(i)) 将上端接线柱i与下端接线柱π(i)相连,如下图。其中,π(i),1≤ i <≤n,是{1,2,…,n}的一个排列。导线(I, π(i))称为该电路板上的第i条连线。对于任何1 ≤ i ≤ j≤n,第i条连线和第j条连线相交的充要条件是π(i)> π(j).
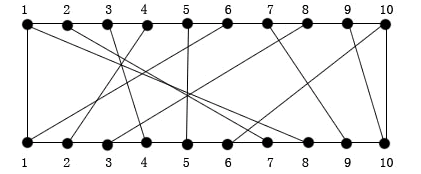
在制作电路板时,要求将这n条线分布到若干个绝缘层上,在同一层上的连线不能相交。电路布线问题要确定将哪些连线安排在第一层上,使得该层上有尽可能多的连线。换句话说,该问题要求确定导线集Nets = {i,π(i),1 ≤ i ≤ n}的最大不想交子集。
书上解决这个问题的时候用了很多集合的概念,我花了一上午的时间去理解,结果没理解啥意思!!!最后还是结合递归式和代码看懂他说的最优子结构性质这一段基本意思。。
定义了一个Size[i][j]二维数组,代表从上端点1,下端点1到上端点i,下端点j之间的最优解。在这样的定义下我们可以求得size[1][j],然后根据定义求得数组上其他值!!最后Size[n][n]就是所求解!!在递推Size[i][j]时,要抓住i条线路在最优解内和不在最优解内做判断。
代码如下:
 #include<windows.h>
#include<windows.h>
 #include<stdio.h>
#include<stdio.h>
 #include<windef.h>
#include<windef.h>
 #include<string.h>
#include<string.h>
 void MNS(int C[],int n,int size[][20])
void MNS(int C[],int n,int size[][20])


 {
{
 int i,j;
int i,j;
 for(j=0;j<C[1];j++) //初始化
for(j=0;j<C[1];j++) //初始化


 {
{
 size[1][j]=0;
size[1][j]=0;
 }
}

 for(j=C[1];j<=n;j++)//初始化
for(j=C[1];j<=n;j++)//初始化


 {
{
 size[1][j]=1;
size[1][j]=1;
 }
}

 for(i=2;i<n;i++) //n>i>=2
for(i=2;i<n;i++) //n>i>=2


 {
{
 for(j=0;j<C[i];j++) //j<C[i]时第i条线路必然不在最优解内
for(j=0;j<C[i];j++) //j<C[i]时第i条线路必然不在最优解内
 size[i][j]=size[i-1][j];
size[i][j]=size[i-1][j];

 for(j=C[i];j<=n;j++)
for(j=C[i];j<=n;j++)
 size[i][j]=max(size[i-1][j],size[i-1][C[i]-1]+1);//取第i条线路在最优解内和不在最优解内的较大值
size[i][j]=max(size[i-1][j],size[i-1][C[i]-1]+1);//取第i条线路在最优解内和不在最优解内的较大值
 }
}

 size[n][n]=max(size[n-1][n],size[n-1][C[n]-1]+1);//书上总喜欢把最后一项单独计算
size[n][n]=max(size[n-1][n],size[n-1][C[n]-1]+1);//书上总喜欢把最后一项单独计算 .有时候是有问题的,就像0-1背包,虽然节约了时间
.有时候是有问题的,就像0-1背包,虽然节约了时间
 }
}

 int Traceback(int C[],int size[][20],int n,int Net[])//构造最优解(从最后一项开始构造)
int Traceback(int C[],int size[][20],int n,int Net[])//构造最优解(从最后一项开始构造)


 {
{
 int j=n,i;
int j=n,i;
 int m=0;
int m=0;
 for(i=n;i>1;i--) //1<i<=n
for(i=n;i>1;i--) //1<i<=n


 {
{
 if(size[i][j]!=size[i-1][j]) //代表第i条入选
if(size[i][j]!=size[i-1][j]) //代表第i条入选


 {
{
 Net[m++]=i;
Net[m++]=i;
 j=C[i]-1; //这里j的目的是为了构造第一条线路是否入选,应为i!=1
j=C[i]-1; //这里j的目的是为了构造第一条线路是否入选,应为i!=1
 }
}
 }
}

 if(j>=C[1]) //入选
if(j>=C[1]) //入选
 Net[m++]=1;
Net[m++]=1;

 return m;
return m;
 }
}

 int main()
int main()


 {
{

 int C[20]=
int C[20]= {0,8,7,4,2,5,1,9,3,10,6},size[20][20],i,j,n,k;
{0,8,7,4,2,5,1,9,3,10,6},size[20][20],i,j,n,k;
 int Net[20];
int Net[20];

 memset(size,0,sizeof(size));
memset(size,0,sizeof(size));
 memset(Net,0,sizeof(Net));
memset(Net,0,sizeof(Net));

 MNS(C,10,size);//构造最优解
MNS(C,10,size);//构造最优解

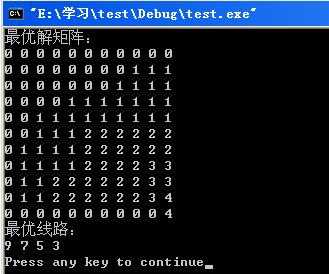
 printf("最优解矩阵:\n");
printf("最优解矩阵:\n");
 n=10;
n=10;
 for(i=0;i<=n;i++)
for(i=0;i<=n;i++)


 {
{
 for(j=0;j<=n;j++)
for(j=0;j<=n;j++)


 {
{
 printf("%d ",size[i][j]);
printf("%d ",size[i][j]);
 }
}
 printf("\n");
printf("\n");
 }
}

 k=Traceback(C,size,n,Net);
k=Traceback(C,size,n,Net);

 printf("最优线路:\n");
printf("最优线路:\n");
 for(i=0;i<k;i++)
for(i=0;i<k;i++)
 printf("%d ",Net[i]);
printf("%d ",Net[i]);
 printf("\n");
printf("\n");


 return 0;
return 0;
 }
} 运行结果如下:
posted on 2010-09-16 12:05
jince 阅读(473)
评论(0) 编辑 收藏 引用 所属分类:
算法设计与分析