数的计数
Time Limit:1000MS Memory Limit:65536K
Total Submit:394 Accepted:183
Description
要求找出具有下列性质数的个数(包括输入的自然数n):
先输入一个自然数n( n <= 1000),然后对此自然数按照如下方法进行处理:
(1)不作任何处理
(2)在它的左边加上一个自然数,但该数不能超过原数的一半
(3)加上数后,继续按此处理,直到不能再加自然数为止
Input
多个测试案例,每个测试案例
输入一个自然数n
Output
输出满足以上条件的所有数的个数
Sample Input
6
Sample Output
6
Hint
对于6,满足条件的数有
6
16
26
126
36
136
这个题目也贴一下,记得书上也有这么个习题的!!
代码如下:
 #include<string.h>
#include<string.h>
 #include<stdio.h>
#include<stdio.h>
 int main()
int main()


 {
{
 int s[1001];
int s[1001];
 int i,j,n;
int i,j,n;
 memset(s,0,sizeof(s));
memset(s,0,sizeof(s));
 s[1]=1;
s[1]=1;
 s[2]=2;
s[2]=2;
 for(i=3;i<1001;i++)
for(i=3;i<1001;i++)


 {
{
 for(j=1;j<=i/2;j++)
for(j=1;j<=i/2;j++)


 {
{
 s[i]=s[j]+s[i];
s[i]=s[j]+s[i];
 }
}
 s[i]++;
s[i]++;
 }
}
 while(scanf("%d",&n)!=EOF)
while(scanf("%d",&n)!=EOF)


 {
{
 printf("%d\n",s[n]);
printf("%d\n",s[n]);
 }
}
 return 0;
return 0;
 }
}

posted @
2010-09-16 12:58 jince 阅读(652) |
评论 (0) |
编辑 收藏
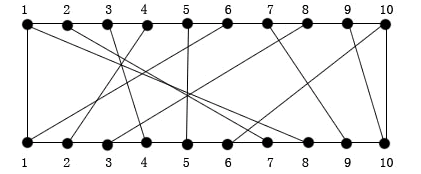
在制作电路板时,要求将这n条线分布到若干个绝缘层上,在同一层上的连线不能相交。电路布线问题要确定将哪些连线安排在第一层上,使得该层上有尽可能多的连线。换句话说,该问题要求确定导线集Nets = {i,π(i),1 ≤ i ≤ n}的最大不想交子集。
书上解决这个问题的时候用了很多集合的概念,我花了一上午的时间去理解,结果没理解啥意思!!!最后还是结合递归式和代码看懂他说的最优子结构性质这一段基本意思。。
定义了一个Size[i][j]二维数组,代表从上端点1,下端点1到上端点i,下端点j之间的最优解。在这样的定义下我们可以求得size[1][j],然后根据定义求得数组上其他值!!最后Size[n][n]就是所求解!!在递推Size[i][j]时,要抓住i条线路在最优解内和不在最优解内做判断。
代码如下:
 #include<windows.h>
#include<windows.h>
 #include<stdio.h>
#include<stdio.h>
 #include<windef.h>
#include<windef.h>
 #include<string.h>
#include<string.h>
 void MNS(int C[],int n,int size[][20])
void MNS(int C[],int n,int size[][20])


 {
{
 int i,j;
int i,j;
 for(j=0;j<C[1];j++) //初始化
for(j=0;j<C[1];j++) //初始化


 {
{
 size[1][j]=0;
size[1][j]=0;
 }
}

 for(j=C[1];j<=n;j++)//初始化
for(j=C[1];j<=n;j++)//初始化


 {
{
 size[1][j]=1;
size[1][j]=1;
 }
}

 for(i=2;i<n;i++) //n>i>=2
for(i=2;i<n;i++) //n>i>=2


 {
{
 for(j=0;j<C[i];j++) //j<C[i]时第i条线路必然不在最优解内
for(j=0;j<C[i];j++) //j<C[i]时第i条线路必然不在最优解内
 size[i][j]=size[i-1][j];
size[i][j]=size[i-1][j];

 for(j=C[i];j<=n;j++)
for(j=C[i];j<=n;j++)
 size[i][j]=max(size[i-1][j],size[i-1][C[i]-1]+1);//取第i条线路在最优解内和不在最优解内的较大值
size[i][j]=max(size[i-1][j],size[i-1][C[i]-1]+1);//取第i条线路在最优解内和不在最优解内的较大值
 }
}

 size[n][n]=max(size[n-1][n],size[n-1][C[n]-1]+1);//书上总喜欢把最后一项单独计算
size[n][n]=max(size[n-1][n],size[n-1][C[n]-1]+1);//书上总喜欢把最后一项单独计算 .有时候是有问题的,就像0-1背包,虽然节约了时间
.有时候是有问题的,就像0-1背包,虽然节约了时间
 }
}

 int Traceback(int C[],int size[][20],int n,int Net[])//构造最优解(从最后一项开始构造)
int Traceback(int C[],int size[][20],int n,int Net[])//构造最优解(从最后一项开始构造)


 {
{
 int j=n,i;
int j=n,i;
 int m=0;
int m=0;
 for(i=n;i>1;i--) //1<i<=n
for(i=n;i>1;i--) //1<i<=n


 {
{
 if(size[i][j]!=size[i-1][j]) //代表第i条入选
if(size[i][j]!=size[i-1][j]) //代表第i条入选


 {
{
 Net[m++]=i;
Net[m++]=i;
 j=C[i]-1; //这里j的目的是为了构造第一条线路是否入选,应为i!=1
j=C[i]-1; //这里j的目的是为了构造第一条线路是否入选,应为i!=1
 }
}
 }
}

 if(j>=C[1]) //入选
if(j>=C[1]) //入选
 Net[m++]=1;
Net[m++]=1;

 return m;
return m;
 }
}

 int main()
int main()


 {
{

 int C[20]=
int C[20]= {0,8,7,4,2,5,1,9,3,10,6},size[20][20],i,j,n,k;
{0,8,7,4,2,5,1,9,3,10,6},size[20][20],i,j,n,k;
 int Net[20];
int Net[20];

 memset(size,0,sizeof(size));
memset(size,0,sizeof(size));
 memset(Net,0,sizeof(Net));
memset(Net,0,sizeof(Net));

 MNS(C,10,size);//构造最优解
MNS(C,10,size);//构造最优解

 printf("最优解矩阵:\n");
printf("最优解矩阵:\n");
 n=10;
n=10;
 for(i=0;i<=n;i++)
for(i=0;i<=n;i++)


 {
{
 for(j=0;j<=n;j++)
for(j=0;j<=n;j++)


 {
{
 printf("%d ",size[i][j]);
printf("%d ",size[i][j]);
 }
}
 printf("\n");
printf("\n");
 }
}

 k=Traceback(C,size,n,Net);
k=Traceback(C,size,n,Net);

 printf("最优线路:\n");
printf("最优线路:\n");
 for(i=0;i<k;i++)
for(i=0;i<k;i++)
 printf("%d ",Net[i]);
printf("%d ",Net[i]);
 printf("\n");
printf("\n");


 return 0;
return 0;
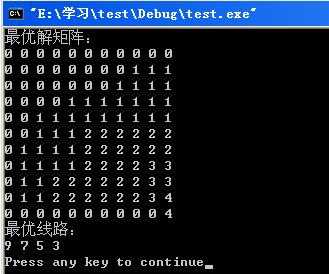
 }
} 运行结果如下:
posted @
2010-09-16 12:05 jince 阅读(474) |
评论 (0) |
编辑 收藏
摘要: 工作的时候写的一个修改记事本的程序段。记录下代码如下:
#include <windows.h>#include <stdio.h>#include <string.h>#include&...
阅读全文
posted @
2010-09-15 09:17 jince 阅读(321) |
评论 (0) |
编辑 收藏
虽然说求最大值最小值函数在哪个头文件下并不是非常重要,但是遇到问题的时候我们很快的找到~~ MSDN上说在algorithm下,但是出错了,其实这两个函数需要包含两个头文件<windows.h>和<windef.h>文件,其他的还有__min和__max需要包含<stdlib.h>头文件。。
 #include <iostream>
#include <iostream>
 #include <windows.h>
#include <windows.h>
 #include <stdio.h>
#include <stdio.h>
 #include <windef.h>
#include <windef.h>
 using namespace std;
using namespace std;


 int main ()
int main ()  {
{
 cout << "max(1,2)==" << max(1,2) << endl;
cout << "max(1,2)==" << max(1,2) << endl;
 cout << "max(2,1)==" << max(2,1) << endl;
cout << "max(2,1)==" << max(2,1) << endl;
 cout << "max('a','z')==" << max('a','z') << endl;
cout << "max('a','z')==" << max('a','z') << endl;
 cout << "max(3.14,2.72)==" << max(3.14,2.72) << endl;
cout << "max(3.14,2.72)==" << max(3.14,2.72) << endl;

 cout << "max(1,2)==" << __max(1,2) << endl;
cout << "max(1,2)==" << __max(1,2) << endl;
 cout << "max(2,1)==" << __max(2,1) << endl;
cout << "max(2,1)==" << __max(2,1) << endl;
 cout << "max('a','z')==" << __max('a','z') << endl;
cout << "max('a','z')==" << __max('a','z') << endl;
 cout << "max(3.14,2.72)==" << __max(3.14,2.72) << endl;
cout << "max(3.14,2.72)==" << __max(3.14,2.72) << endl;
 return 0;
return 0;
 }
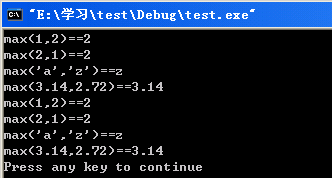
}运行结果如下:
posted @
2010-09-14 15:59 jince 阅读(27722) |
评论 (4) |
编辑 收藏免费馅饼
Time Limit:1000MS Memory Limit:65536K
Total Submit:615 Accepted:149
Description
都说天上不会掉馅饼,但有一天gameboy正走在回家的小径上,忽然天上掉下大把大把的馅饼。说来gameboy的人品实在是太好了,这馅饼别处都不掉,就掉落在他身旁的10米范围内。馅饼如果掉在了地上当然就不能吃了,所以gameboy马上卸下身上的背包去接。但由于小径两侧都不能站人,所以他只能在小径上接。由于gameboy平时老呆在房间里玩游戏,虽然在游戏中是个身手敏捷的高手,但在现实中运动神经特别迟钝,每秒种只有在移动不超过一米的范围内接住坠落的馅饼。现在给这条小径如图标上坐标:

为了使问题简化,假设在接下来的一段时间里,馅饼都掉落在0-10这11个位置。开始时gameboy站在5这个位置,因此在第一秒,他只能接到4,5,6这三个位置中期中一个位置上的馅饼。问gameboy最多可能接到多少个馅饼?(假设他的背包可以容纳无穷多个馅饼)
Input
输入数据有多组。每组数据的第一行为以正整数n(0 < n < 100000),表示有n个馅饼掉在这条小径上。在结下来的n行中,每行有两个整数x,T(0 <= T < 100000),表示在第T秒有一个馅饼掉在x点上。同一秒钟在同一点上可能掉下多个馅饼。n=0时输入结束。
Output
每一组输入数据对应一行输出。输出一个整数m,表示gameboy最多可能接到m个馅饼。
提示:本题的输入数据量比较大,建议用scanf读入,用cin可能会超时。
Sample Input
6
5 1
4 1
6 1
7 2
7 2
8 3
0
Sample Output
4
Source
hdu1176
这个题目也属于简单的动态规划题目,如果直观的从深度搜索的方法去做可能会超时,很多时候我们采用数组填表的方式求解,以空间换取时间!!
如果这个题目还有个小变化,就是捡饼人一开始站在5号位置,所以如果往我们直接从上往下求,只能求得最后每个点上的最优值,所以我们应该从后往前求,求得第一秒的时候每个点上的最优值,也就是题目要求的解!!
代码如下:
 #include<cstdio>
#include<cstdio>
 #include<cstdlib>
#include<cstdlib>
 #include<cstring>
#include<cstring>
 int time[100001][11];
int time[100001][11];
 int max(int x,int y,int z)
int max(int x,int y,int z)


 {
{
 if(x>y)
if(x>y)
 if(x>z)
if(x>z)
 return x;
return x;
 else
else
 return z;
return z;
 else
else
 if(y>z)
if(y>z)
 return y;
return y;
 else
else
 return z;
return z;
 }
}
 int main()
int main()


 {
{
 int i,j,k,n,x,y;
int i,j,k,n,x,y;
 while(scanf("%d",&n)!=EOF&&n!=0)
while(scanf("%d",&n)!=EOF&&n!=0)


 {
{
 memset(time,0,sizeof(time));
memset(time,0,sizeof(time));
 k=0;
k=0;
 for(i=0;i<n;i++)
for(i=0;i<n;i++)


 {
{
 scanf("%d %d",&y,&x);
scanf("%d %d",&y,&x);
 time[x][y]++;
time[x][y]++;
 if(x>k)
if(x>k)
 k=x;
k=x;
 }
}


 /**//* for(i=2;i<k'i++)
/**//* for(i=2;i<k'i++)
 {
{
 for(j=0;j<11;j++)
for(j=0;j<11;j++)
 {
{
 if(j>0&&j<10)
if(j>0&&j<10)
 time[i][j]+=max(time[i-1][j-1],time[i-1][j],time[i-1][j+1]);
time[i][j]+=max(time[i-1][j-1],time[i-1][j],time[i-1][j+1]);
 else if(j==0)
else if(j==0)
 time[i][j]+=max(0,time[i-1][j],time[i-1][j+1]);
time[i][j]+=max(0,time[i-1][j],time[i-1][j+1]);
 else
else
 time[i][j]+=max(0,time[i-1][j-1],time[i-1][j]);
time[i][j]+=max(0,time[i-1][j-1],time[i-1][j]);
 }
}
 }*/
}*/
 for(i=k-1;i>=0;i--)
for(i=k-1;i>=0;i--)


 {
{
 for(j=0;j<11;j++)
for(j=0;j<11;j++)


 {
{
 if(j>0&&j<10)
if(j>0&&j<10)
 time[i][j]+=max(time[i+1][j-1],time[i+1][j],time[i+1][j+1]);
time[i][j]+=max(time[i+1][j-1],time[i+1][j],time[i+1][j+1]);
 else if(j==0)
else if(j==0)
 time[i][j]+=max(0,time[i+1][j],time[i+1][j+1]);
time[i][j]+=max(0,time[i+1][j],time[i+1][j+1]);
 else
else
 time[i][j]+=max(0,time[i+1][j-1],time[i+1][j]);
time[i][j]+=max(0,time[i+1][j-1],time[i+1][j]);
 }
}
 }
}
 printf("%d\n",time[0][5]);
printf("%d\n",time[0][5]);
 }
}
 return 0;
return 0;
 }
}

posted @
2010-09-14 15:22 jince 阅读(1267) |
评论 (2) |
编辑 收藏计算直线的交点数
Time Limit:1000MS Memory Limit:65536K
Total Submit:260 Accepted:119
Description
平面上有n条直线,且无三线共点,问这些直线能有多少种不同交点数。
比如,如果n=2,则可能的交点数量为0(平行)或者1(不平行)。
Input
输入数据包含多个测试实例,每个测试实例占一行,每行包含一个正整数n(n <= 20),n表示直线的数量.
Output
每个测试实例对应一行输出,从小到大列出所有相交方案,其中每个数为可能的交点数,每行的整数之间用一个空格隔开。
Sample Input
2
3
Sample Output
0 1
0 2 3
Source
hdu1466
题目意思很明确,网上有很多的解释都差不多,我记得从前我做这个题目的时候感到很纠结,主要还是看代码的时候不容易看懂,现在稍微好一点了,总之一定要自己去画,这样才会理解!!
网上代码如下(我再解释一下):
 #include<stdio.h>
#include<stdio.h>
 #include<string.h>
#include<string.h>
 int main()
int main()


 {
{
 int i,j,n,f[21][191]; //f[i][j]代表i条直线是否能产生j个交点,如果能f[i][j]=1,否则为0;
int i,j,n,f[21][191]; //f[i][j]代表i条直线是否能产生j个交点,如果能f[i][j]=1,否则为0;

 memset(f,0,sizeof(f));
memset(f,0,sizeof(f));

 for(i=0;i<21;i++) //零个交点置零
for(i=0;i<21;i++) //零个交点置零
 f[i][0]=1;
f[i][0]=1;

 for(n=2;n<21;n++) //从两条直线开始求
for(n=2;n<21;n++) //从两条直线开始求
 for(i=n-1;i>=1;i--) //取出n-i条做变化
for(i=n-1;i>=1;i--) //取出n-i条做变化
 for(j=0;j<191;j++) //j变化
for(j=0;j<191;j++) //j变化
 if(f[n-i][j]==1) //如果取出的n-i条能过产生j个交点,置f[n][j+(n-i)*i]=1,j+(n-i)*i为取出n-i条直线做变化情况下的交点数
if(f[n-i][j]==1) //如果取出的n-i条能过产生j个交点,置f[n][j+(n-i)*i]=1,j+(n-i)*i为取出n-i条直线做变化情况下的交点数
 f[n][j+(n-i)*i]=1;
f[n][j+(n-i)*i]=1;

 while(scanf("%d",&n)!=EOF)
while(scanf("%d",&n)!=EOF)


 {
{
 printf("0");
printf("0");

 for(j=1;j<=n*(n-1)/2;j++) //统计
for(j=1;j<=n*(n-1)/2;j++) //统计
 if(f[n][j])
if(f[n][j])
 printf(" %d",j);
printf(" %d",j);

 printf("\n");
printf("\n");
 }
}

 return 0;
return 0;
 }
}
其实可以直接这么写,容易理解一点。。
代码如下:
 #include<string.h>
#include<string.h>
 #include<stdio.h>
#include<stdio.h>
 int main()
int main()


 {
{
 int i,j,n;
int i,j,n;
 int f[21][191];
int f[21][191];

 memset(f,0,sizeof(f));
memset(f,0,sizeof(f));

 for(i=1;i<21;i++)
for(i=1;i<21;i++)
 f[i][0]=1;
f[i][0]=1;

 for(j=1;j<191;j++)
for(j=1;j<191;j++)
 f[1][j]=0;
f[1][j]=0;

 for(n=2;n<21;n++)
for(n=2;n<21;n++)


 {
{
 for(i=1;i<n;i++)
for(i=1;i<n;i++)


 {
{
 for(j=0;j<191;j++)
for(j=0;j<191;j++)


 {
{
 if(f[i][j])
if(f[i][j])


 {
{
 f[n][j+i*(n-i)]=1;
f[n][j+i*(n-i)]=1;
 }
}
 }
}
 }
}
 }
}

 while(scanf("%d",&n)!=EOF)
while(scanf("%d",&n)!=EOF)


 {
{
 printf("0");
printf("0");
 for(j=1;j<=n*(n-1)/2;j++)
for(j=1;j<=n*(n-1)/2;j++)


 {
{
 if(f[n][j])
if(f[n][j])
 printf(" %d",j);
printf(" %d",j);
 }
}
 printf("\n");
printf("\n");
 }
}
 return 0;
return 0;
 }
}

posted @
2010-09-14 10:46 jince 阅读(981) |
评论 (0) |
编辑 收藏
C语言中的time:
代码如下:
 #include<stdio.h>
#include<stdio.h>
 #include<time.h>
#include<time.h>
 int main()
int main()


 {
{
 time_t timep;
time_t timep;
 time(&timep);
time(&timep);
 printf("%d\n",gmtime(&timep));
printf("%d\n",gmtime(&timep));
 printf("%s\n",asctime(gmtime(&timep)));
printf("%s\n",asctime(gmtime(&timep)));
 printf("%s\n",ctime(&timep));
printf("%s\n",ctime(&timep));
 return 0;
return 0;
 }
} 数据字节数输出:
代码如下:
 #include<stdio.h>
#include<stdio.h>
 int main()
int main()


 {
{
 printf("char %d\n",sizeof(char));
printf("char %d\n",sizeof(char));
 printf("int %d\n",sizeof(int));
printf("int %d\n",sizeof(int));
 printf("short int %d\n",sizeof(short int));
printf("short int %d\n",sizeof(short int));
 printf("long int %d\n",sizeof(long int));
printf("long int %d\n",sizeof(long int));
 printf("float %d\n",sizeof(float));
printf("float %d\n",sizeof(float));
 printf("double %d\n",sizeof(double));
printf("double %d\n",sizeof(double));
 return 0;
return 0;
 }
} printf输出格式:
代码如下:
 #include<cstdio>
#include<cstdio>
 int main()
int main()


 {
{
 //for int
//for int
 int i=30122121;
int i=30122121;
 long i2=309095024;
long i2=309095024;
 short i3=30;
short i3=30;
 unsigned i4=2123453;
unsigned i4=2123453;
 printf("%d,%o,%x,%X,%ld,%hd,%u\n",i,i,i,i,i2,i3,i4);//如果是:%l,%h,则输不出结果
printf("%d,%o,%x,%X,%ld,%hd,%u\n",i,i,i,i,i2,i3,i4);//如果是:%l,%h,则输不出结果
 printf("%d,%ld\n",i,i2);//试验不出%ld和%d之间的差别,因为long是4bytes
printf("%d,%ld\n",i,i2);//试验不出%ld和%d之间的差别,因为long是4bytes
 printf("%hd,%hd\n\n\n",i,i3);//试验了%hd和%d之间的差别,因为short是2bytes
printf("%hd,%hd\n\n\n",i,i3);//试验了%hd和%d之间的差别,因为short是2bytes

 //for string and char
//for string and char
 char ch1='d';
char ch1='d';
 unsigned char ch2=160;
unsigned char ch2=160;
 char *str="Hello everyone!";
char *str="Hello everyone!";
 printf("%c,%u,%s\n\n\n",ch1,ch2,str);//unsigned char超过128的没有字符对应
printf("%c,%u,%s\n\n\n",ch1,ch2,str);//unsigned char超过128的没有字符对应

 //for float and double,unsigned and signed can not be used with double and float
//for float and double,unsigned and signed can not be used with double and float
 float fl=2.566545445F;//or 2.566545445f
float fl=2.566545445F;//or 2.566545445f
 double dl=265.5651445;
double dl=265.5651445;
 long double dl2=2.5654441454;
long double dl2=2.5654441454;

 //%g没有e格式,默认6位包括小数点前面的数,
//%g没有e格式,默认6位包括小数点前面的数,
 //%f没有e格式,默认6位仅只小数点后面包含6位
//%f没有e格式,默认6位仅只小数点后面包含6位
 //%e采用e格式,默认6位为转化后的小数点后面的6位
//%e采用e格式,默认6位为转化后的小数点后面的6位
 printf("%f,%e,%g,%.7f\n",fl,dl,dl,dl);
printf("%f,%e,%g,%.7f\n",fl,dl,dl,dl);
 printf("%f,%E,%G,%f\n",fl,dl,dl,dl);//%F is wrong
printf("%f,%E,%G,%f\n",fl,dl,dl,dl);//%F is wrong
 printf("%.8f,%.10e\n",fl,dl);
printf("%.8f,%.10e\n",fl,dl);
 printf("%.8e,%.10f\n\n\n",fl,dl);
printf("%.8e,%.10f\n\n\n",fl,dl);

 //for point
//for point
 int *iP=&i;
int *iP=&i;
 char *iP1=new char;
char *iP1=new char;
 void *iP2;//dangerous!
void *iP2;//dangerous!
 printf("%p,%p,%p\n\n\n",iP,iP1,iP2);
printf("%p,%p,%p\n\n\n",iP,iP1,iP2);

 //其他知识:负号,表示左对齐(默认是右对齐);%6.3,6表示宽度,3表示精度
//其他知识:负号,表示左对齐(默认是右对齐);%6.3,6表示宽度,3表示精度
 char *s="Hello world!";
char *s="Hello world!";
 printf(":%s: \n:%10s: \n:%.10s: \n:%-10s: \n:%.15s: \n:%-15s: \n:%15.10s: \n:%-15.10s:\n\n\n",
printf(":%s: \n:%10s: \n:%.10s: \n:%-10s: \n:%.15s: \n:%-15s: \n:%15.10s: \n:%-15.10s:\n\n\n",
 s,s,s,s,s,s,s,s);
s,s,s,s,s,s,s,s);
 double ddd=563.908556444;
double ddd=563.908556444;
 printf(":%g: \n:%10g: \n:%.10g: \n:%-10g: \n:%.15g: \n:%-15g: \n:%15.10g: \n:%-15.10g:\n\n\n",
printf(":%g: \n:%10g: \n:%.10g: \n:%-10g: \n:%.15g: \n:%-15g: \n:%15.10g: \n:%-15.10g:\n\n\n",
 ddd,ddd,ddd,ddd,ddd,ddd,ddd,ddd);
ddd,ddd,ddd,ddd,ddd,ddd,ddd,ddd);

 //还有一个特殊的格式%*.* ,这两个星号的值分别由第二个和第三个参数的值指定
//还有一个特殊的格式%*.* ,这两个星号的值分别由第二个和第三个参数的值指定
 printf("%.*s \n", 8, "abcdefgggggg");
printf("%.*s \n", 8, "abcdefgggggg");
 printf("%*.*f \n", 3,3, 1.25456f);
printf("%*.*f \n", 3,3, 1.25456f);
 return 0;
return 0;
 }
}posted @
2010-09-14 10:06 jince 阅读(248) |
评论 (0) |
编辑 收藏去北京看奥运
Time Limit:1000MS Memory Limit:65536K
Total Submit:398 Accepted:116
Description
2008年将到,王飞同学化了九牛二虎之力搞到了2张2008年奥运会足球赛决赛的门票。真是开心啊!他爸爸准备开车跟他一起去北京看球赛。不过门票费好贵啊,所以他爸爸说了,这个钱要在下学期的生活费里扣(好抠门),不过如果他能让从杭州去北京的油费最省(油价最近涨的好厉害啊),那么就不扣生活费了。
哈哈,这个就难不倒他了。在ACM里可不是白混的。
很快他算出了汽车从杭州到北京必须要加几次油,并查出了到北京要经过哪几个城市,每个城市有哪些加油站以及从某城市各加油站到另一城市各加油站的距离和路况算出了各加油站之间的耗油量。
下面是不是很easy?

Input
有多个测试案例。第一行先输入测试案例的数目T。
对于每个测试案例,第一行输入一个整数n表示将在中途n(0 < n < 40)个城市中加油,后面紧跟着是n个整数代表每个城市有几个加油站(每个城市加油站不超过10个)。
以下n+1行,每行由3个Si,Ej,L一组组成的好几对整数,该行以0结束。表示从前一城市Si第i个加油站(杭州的话就是家拉)出发到该城市第j个加油站消耗的油量为L升。
Output
对于每个测试,输出一行,内容为最小总耗油量。
Sample Input
1
2 2 3
1 1 3 1 2 1 0
1 1 2 1 2 7 2 1 8 2 2 9 2 3 4 0
1 1 5 2 1 6 3 1 6 0
Sample Output
10
中文题,这种是最简单的动态规划问题了,从左往右折,每次求得各个加油站上最小耗油量!!!
看代码的时候发现自己写的看不懂了。。。。悲剧!!!代码实现能力仍然是个话题啊!!
代码如下:
 #include<stdio.h>
#include<stdio.h>
 #include<string.h>
#include<string.h>
 int main()
int main()


 {
{
 int num1[50];
int num1[50];
 int num2[50]; //暂时存储中间结果
int num2[50]; //暂时存储中间结果
 int num3[50]; //结果数组
int num3[50]; //结果数组
 int t,n,k,s,e,i,g,m,j;
int t,n,k,s,e,i,g,m,j;
 int l;
int l;
 scanf("%d",&t); //组数
scanf("%d",&t); //组数
 for(m=0;m<t;m++)
for(m=0;m<t;m++)


 {
{
 for(j=0;j<15;j++) //初始化num3
for(j=0;j<15;j++) //初始化num3
 num3[j]=0;
num3[j]=0;

 scanf("%d",&n); //城市个数
scanf("%d",&n); //城市个数

 for(i=0;i<n;i++) //城市加油站个数没用。。。
for(i=0;i<n;i++) //城市加油站个数没用。。。
 scanf("%d",&k);
scanf("%d",&k);

 for(i=0;i<n+1;i++) //n个城市要走n步
for(i=0;i<n+1;i++) //n个城市要走n步


 {
{
 for(j=0;j<15;j++) //初始化
for(j=0;j<15;j++) //初始化
 num2[j]=1000000;
num2[j]=1000000;

 for(j=0;j<15;j++) //初始化
for(j=0;j<15;j++) //初始化
 num1[j]=0;
num1[j]=0;

 while(scanf("%d",&g)!=EOF&&g!=0)//参数判定
while(scanf("%d",&g)!=EOF&&g!=0)//参数判定


 {
{
 s=g;
s=g;
 scanf("%d %d",&e,&l);
scanf("%d %d",&e,&l);

 if(num2[e]==1000000)
if(num2[e]==1000000)


 {
{
 num1[e]=num3[s]+l;
num1[e]=num3[s]+l;
 num2[e]=num1[e];
num2[e]=num1[e];
 }
}

 else if(num3[s]+l<=num2[e])
else if(num3[s]+l<=num2[e])


 {
{
 num1[e]=num3[s]+l;
num1[e]=num3[s]+l;
 num2[e]=num1[e];
num2[e]=num1[e];
 }
}

 }
}

 for(j=0;j<50;j++) //结果存储
for(j=0;j<50;j++) //结果存储
 num3[j]=num2[j];
num3[j]=num2[j];

 }
}

 printf("%d\n",num3[1]); //输出结果
printf("%d\n",num3[1]); //输出结果
 }
}
 return 0;
return 0;
 }
}
posted @
2010-09-14 09:59 jince 阅读(331) |
评论 (0) |
编辑 收藏
学以致用!!!
随机数可以用来计算概率,面积等!!
一、随机数,模拟抛硬币正面时间频率图。
代码如下:
 #include<iostream>
#include<iostream>
 #include<time.h>
#include<time.h>
 using namespace std;
using namespace std;
 const unsigned long maxshort=65536L;
const unsigned long maxshort=65536L;
 const unsigned long multiplier=1194211693L;
const unsigned long multiplier=1194211693L;
 const unsigned long adder=12345L;
const unsigned long adder=12345L;

 class RandomNumber
class RandomNumber


 {
{
 private:
private:
 unsigned long randSeed; //随机种子
unsigned long randSeed; //随机种子
 public:
public:
 RandomNumber(unsigned long s=0); //构造函数,为randSeed置数
RandomNumber(unsigned long s=0); //构造函数,为randSeed置数
 unsigned short Random(unsigned long n); //获取0~n的一个随机数
unsigned short Random(unsigned long n); //获取0~n的一个随机数
 double fRandom(void); //获取一个小数
double fRandom(void); //获取一个小数
 };
};

 RandomNumber::RandomNumber(unsigned long s)
RandomNumber::RandomNumber(unsigned long s)


 {
{
 if(s==0)
if(s==0)
 randSeed=time(0); //这里获取直接用time函数获取了一个时间值当做种子了,没有再用srand函数构造种子了!网上查了下time()函数为从1970年1月1日0时0分0秒到此时的秒数!!!
randSeed=time(0); //这里获取直接用time函数获取了一个时间值当做种子了,没有再用srand函数构造种子了!网上查了下time()函数为从1970年1月1日0时0分0秒到此时的秒数!!!
 else
else
 randSeed=s;
randSeed=s;
 }
}

 unsigned short RandomNumber::Random(unsigned long n)
unsigned short RandomNumber::Random(unsigned long n)


 {
{
 // printf("randSeed:%lu \nmultiplier:%lu \nrandSeed*multiplier:%lu\n",randSeed,multiplier,randSeed*multiplier);
// printf("randSeed:%lu \nmultiplier:%lu \nrandSeed*multiplier:%lu\n",randSeed,multiplier,randSeed*multiplier);
 randSeed=multiplier*randSeed+adder; //这里存在一个越界问题,但是还是会从新获得一个randSeed
randSeed=multiplier*randSeed+adder; //这里存在一个越界问题,但是还是会从新获得一个randSeed
 // printf("(randSeed>>16):%lu\n",randSeed>>16);
// printf("(randSeed>>16):%lu\n",randSeed>>16);
 return (unsigned short)((randSeed>>16)%n); //右移16为再与n取余,从而获得一个0~n的随机数,其实我还不明白,为啥还要右移呢?难道是为了随机性?
return (unsigned short)((randSeed>>16)%n); //右移16为再与n取余,从而获得一个0~n的随机数,其实我还不明白,为啥还要右移呢?难道是为了随机性?
 }
}

 double RandomNumber::fRandom(void)
double RandomNumber::fRandom(void)


 {
{
 return Random(maxshort)/double(maxshort);
return Random(maxshort)/double(maxshort);
 }
}

 int TossCoins(int numberCoins)
int TossCoins(int numberCoins)


 {
{
 static RandomNumber coinToss; //注意了这里定义了一个静态变量,在函数反复调用中coinToss的属性值不变,从构造函数的角度来理解,在函数反复调用过程中,该对象是不会重新去构造的(不会重复调用构造函数的)!
static RandomNumber coinToss; //注意了这里定义了一个静态变量,在函数反复调用中coinToss的属性值不变,从构造函数的角度来理解,在函数反复调用过程中,该对象是不会重新去构造的(不会重复调用构造函数的)!
 int i,tosses=0;
int i,tosses=0;
 for(i=0;i<numberCoins;i++) //这里调用Random函数!!
for(i=0;i<numberCoins;i++) //这里调用Random函数!!


 {
{
 tosses+=coinToss.Random(2); //返回0或1,1表示正面,0表示反面,累计正面朝上的次数
tosses+=coinToss.Random(2); //返回0或1,1表示正面,0表示反面,累计正面朝上的次数
 }
}
 return tosses; //返回正面朝上的次数
return tosses; //返回正面朝上的次数
 }
}
 void main()
void main()


 {
{
 const int NCOINS=10; //定义了常量,我从一些牛人哪里看到,我们应该把静态变量看成只读。。。
const int NCOINS=10; //定义了常量,我从一些牛人哪里看到,我们应该把静态变量看成只读。。。
 const long NTOSSES=50000L;
const long NTOSSES=50000L;
 long i,heads[NCOINS+1]; //h[i]代表NTOSSES次抛NCOINS次抛硬币中i次正面次数,貌似有些拗口,按这个实例来说,应该是做50000次抛10次硬币,然后统计10次中出现0次正面朝上次数,1次正面朝上次数,。。10次正面朝上次数
long i,heads[NCOINS+1]; //h[i]代表NTOSSES次抛NCOINS次抛硬币中i次正面次数,貌似有些拗口,按这个实例来说,应该是做50000次抛10次硬币,然后统计10次中出现0次正面朝上次数,1次正面朝上次数,。。10次正面朝上次数
 int j,position;
int j,position;

 for(j=0;j<NCOINS+1;j++)
for(j=0;j<NCOINS+1;j++)
 heads[j]=0;
heads[j]=0;

 for(i=0;i<NTOSSES;i++) //累计
for(i=0;i<NTOSSES;i++) //累计
 heads[TossCoins(NCOINS)]++;
heads[TossCoins(NCOINS)]++;

 cout<<"head结果:";
cout<<"head结果:";
 for(i=0;i<=NCOINS;i++) //输出h结果
for(i=0;i<=NCOINS;i++) //输出h结果


 {
{
 cout<<heads[i]<<" ";
cout<<heads[i]<<" ";
 }
}

 cout<<endl;
cout<<endl;

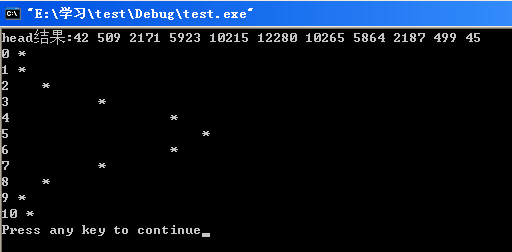
 for(i=0;i<=NCOINS;i++) //模拟抛硬币正面事件平率图
for(i=0;i<=NCOINS;i++) //模拟抛硬币正面事件平率图


 {
{
 position=int (float(heads[i])/NTOSSES*100);//这里有强制类型转换,其实这里计算了概率,通过强制类型转换成整数!!!
position=int (float(heads[i])/NTOSSES*100);//这里有强制类型转换,其实这里计算了概率,通过强制类型转换成整数!!!
 cout<<i<<" ";
cout<<i<<" ";

 for(j=0;j<position-1;j++) //输出空格
for(j=0;j<position-1;j++) //输出空格
 cout<<" ";
cout<<" ";
 cout<<"*"<<endl;
cout<<"*"<<endl;
 }
}
 }
}运行结果如下:
二、随机数,计算∏。基本思想也是运用了概率事件!设有一个半径为r的圆及其外切四边形,向该图形投掷N个点。设落入圆内的点数为K,由于投入的点在正方形上分布均匀,所以落入圆中的概率为∏*R^2/4/R^2,从投点的角度考虑,该概率为K/N,当N足够大时,我们可以近似的认为二者相等。从而∏=4*K/N。
代码如下:
 double Darts(int n)
double Darts(int n)


 {
{
 static RandomNumber dart;
static RandomNumber dart;
 int k=0;
int k=0;
 for(int i=1;i<=n;i++)
for(int i=1;i<=n;i++)


 {
{
 double x=dart.fRandom();
double x=dart.fRandom();
 double y=dart.fRandom();
double y=dart.fRandom();
 if((x*x+y*y)<=1)
if((x*x+y*y)<=1)
 k++;
k++;
 }
}
 return 4*k/double(n);
return 4*k/double(n);
 }
}当n=500000000时,运行结果如下:
printf输出:
http://hi.baidu.com/jiaju111/blog/item/dcd7fd8ba9a7fa1ac9fc7ae2.htmlC语言时间日期函数说明:
http://www.cnblogs.com/neonlight/archive/2008/08/22/1273942.html
posted @
2010-09-13 15:51 jince 阅读(670) |
评论 (0) |
编辑 收藏
在别人眼里轻而易举的的事情落在自己身上可能比登天还要难!!
0-1背包问题:给定n中物品和一个背包。物品i的重量是wi,价值为vi,背包的容量为c。问如何选择装入背包中的武平,使得装入背包中的物品价值最大?
书上有一行行的算式,证明最优子结构性质和构造递归关系。我没怎么看明白最优子结构,但是我能看懂递归关系式!!我记得当时老师叫我们的时候我自己想了好几天才想明白这个递归式,但是始终觉得有点虚,借此我再写一下!
设数组m(i,j)代表背包容量为j,可选物品为i,i+1,..n时的最优解(这里的最优解指的是选择方案,并非正真的最优值),显然m(1,c)是0-1背包问题的解(
这里是书上的错误,应该是m[1]中的最大值!!我后来才发现的。。)。这种定义虽然比较拗口,但是还是可以接受的,其实我们也可以这么定义m[i][j],代表背包容量为j,当前选择物品为a[i]时的最优解,显然m数组中第n行的最大值是0-1背包问题的解!!
第一种定义的递归式如下:
0 1
m[i][j]=max{m[i+1][j],m[i+1][j-wi]+vi} j>=wi; m[i][j]=m(i+1,j) 0<=j<wi
第二种定义的递归式如下:
0 1 m[i][j]=max{m[i-1][j],m[i-1][j-wi]+vi} j>=wi; m[i][j]=m(i-1,j) 0<=j<wi
代码如下:
 #include<stdio.h>
#include<stdio.h>
 #include<iostream>
#include<iostream>
 #include<string.h>
#include<string.h>
 using namespace std;
using namespace std;

 int max(int x,int y)
int max(int x,int y)


 {
{
 if(x>y)
if(x>y)
 return x;
return x;
 return y;
return y;
 }
}

 int min(int x,int y)
int min(int x,int y)


 {
{
 if(x>y)
if(x>y)
 return y;
return y;
 return x;
return x;
 }
}

 template <class Type>
template <class Type>
 void Knapsack(Type *v,int *w,int c,int n,Type m[][20])//构造m,最优取舍方案函数!!
void Knapsack(Type *v,int *w,int c,int n,Type m[][20])//构造m,最优取舍方案函数!!


 {
{
 int i,j;
int i,j;
 int jMax=min(w[n]-1,c);
int jMax=min(w[n]-1,c);

 for(j=0;j<=jMax;j++)
for(j=0;j<=jMax;j++)
 m[n][j]=0;
m[n][j]=0;

 for(j=w[n];j<=c;j++)
for(j=w[n];j<=c;j++)
 m[n][j]=v[n];
m[n][j]=v[n];

 for(i=n-1;i>=1;i--)
for(i=n-1;i>=1;i--)


 {
{
 jMax=min(w[i]-1,c);
jMax=min(w[i]-1,c);

 for(j=0;j<jMax;j++)
for(j=0;j<jMax;j++)
 m[i][j]=m[i+1][j];
m[i][j]=m[i+1][j];

 for(j=w[i];j<=c;j++)
for(j=w[i];j<=c;j++)
 m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
 }
}


 /**//* m[1][c]=m[2][c];
/**//* m[1][c]=m[2][c];
 if(c>=w[1])
if(c>=w[1])
 m[1][c]=max(m[1][c],m[2][c-w[1]]+v[1]);*///这里是书上的一个错误,并不是m[1][c]就是0-1背包问题的解,事实上m[1]上的所有解都有可能!!
m[1][c]=max(m[1][c],m[2][c-w[1]]+v[1]);*///这里是书上的一个错误,并不是m[1][c]就是0-1背包问题的解,事实上m[1]上的所有解都有可能!!
 //所以还是应该把m[1]上的所有最优构造都算出来,然后去最大值
//所以还是应该把m[1]上的所有最优构造都算出来,然后去最大值
 }
}

 template <class Type> //构造x数组函数
template <class Type> //构造x数组函数
 void Traceback(Type m[][20],int *w,int c,int n,int x[])
void Traceback(Type m[][20],int *w,int c,int n,int x[])


 {
{
 int i;
int i;
 for(i=1;i<n;i++)
for(i=1;i<n;i++)


 {
{
 if(m[i][c]==m[i+1][c])
if(m[i][c]==m[i+1][c])
 x[i]=0;
x[i]=0;
 else
else


 {
{
 x[i]=1;
x[i]=1;
 c-=w[i];
c-=w[i];
 }
}
 }
}

 x[n]=(m[n][c])?1:0;
x[n]=(m[n][c])?1:0;
 }
}
 int main()
int main()


 {
{
 int w[10],v[10],x[10],m[20][20],c,n,max,c0;
int w[10],v[10],x[10],m[20][20],c,n,max,c0;
 int i,j;
int i,j;

 while(scanf("%d",&n)!=EOF)
while(scanf("%d",&n)!=EOF)


 {
{
 max=0;
max=0;
 memset(m,0,sizeof(m));
memset(m,0,sizeof(m));
 for(i=1;i<=n;i++)
for(i=1;i<=n;i++)


 {
{
 scanf("%d %d",&w[i],&v[i]);
scanf("%d %d",&w[i],&v[i]);
 }
}
 scanf("%d",&c);
scanf("%d",&c);

 Knapsack(v,w,c,n,m); //构造最优取舍方案
Knapsack(v,w,c,n,m); //构造最优取舍方案

 for(i=1;i<=c;i++)
for(i=1;i<=c;i++)


 {
{
 if(m[1][i]>max)
if(m[1][i]>max)


 {
{
 max=m[1][i];
max=m[1][i];
 c0=i;
c0=i;
 }
}
 }
}
 Traceback(m,w,c0,n,x); //构造x数组
Traceback(m,w,c0,n,x); //构造x数组

 printf("最优矩阵如下:\n");
printf("最优矩阵如下:\n");
 for(i=1;i<=n;i++)
for(i=1;i<=n;i++)


 {
{
 for(j=0;j<=c;j++)
for(j=0;j<=c;j++)
 printf("%d ",m[i][j]);
printf("%d ",m[i][j]);
 printf("\n");
printf("\n");
 }
}

 printf("方案如下:\n");
printf("方案如下:\n");
 for(i=1;i<=n;i++)
for(i=1;i<=n;i++)
 printf("%d ",x[i]);
printf("%d ",x[i]);
 printf("\n");
printf("\n");
 }
}
 return 0;
return 0;
 }
}运行结果如下:
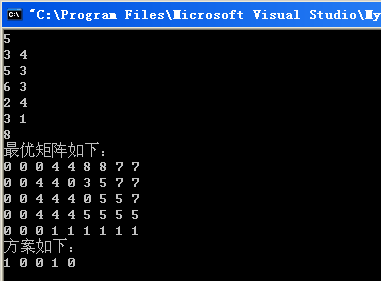
第二种递归思路下的代码和运行过程我就不写,就初始化和递归次序不同!!
我一个同学经常跟我说,以后自己有孩子,一个赚了1000给我花100,一个赚了10000给我花200,我还是跟着赚1000的吧!!其实问题不在别人,而在自己,努力就成!!!我受益匪浅。。。
posted @
2010-09-11 16:32 jince 阅读(1872) |
评论 (0) |
编辑 收藏