这个题目，我们让老师鄙视了。。。
Description
Famous Harry Potter,who seemd to be a normal and poor boy,is actually a wizard.Everything changed when he had his birthday of ten years old.A huge man called 'Hagrid' found Harry and lead him to a new world full of magic power.
If you've read this story,you probably know that Harry's parents had left him a lot of gold coins.Hagrid lead Harry to Gringotts(the bank hold up by Goblins). And they stepped into the room which stored the fortune from his father.Harry was astonishing ,coz there were piles of gold coins.
The way of packing these coins by Goblins was really special.Only one coin was on the top,and three coins consisted an triangle were on the next lower layer.The third layer has six coins which were also consisted an triangle,and so on.On the ith layer there was an triangle have i coins each edge(totally i*(i+1)/2).The whole heap seemed just like a pyramid.Goblin still knew the total num of the layers,so it's up you to help Harry to figure out the sum of all the coins.
Input
The input will consist of some cases,each case takes a line with only one integer N( 0 < N < 2^31).It ends with a single 0.
Output
For each test case, output a line contains the number of all the coins, the format like the sample out(2 decimal digits).
Sample Input
1
3
0
Sample Output
1.00E0
1.00E1
Hint
when N=1 ,There is 1 gold coins.
when N=3 ,There is 1+3+6=10 gold coins.
题目很简单，求Sn=i*(i+1)/2的前n项和，n由题目给出。
平方和公式：1^2+2^2+3^2+...+n^2=n(n+1)(2*n+1)/6 等差求和：1+2+3+...+n=n*(n+1)/2
代码如下：
#include<stdio.h>
#include<math.h>
int main()
{
double test,sum;
int i;
scanf("%lf",&test);
while(test!=0)
{
sum=((test*(test+1)*(2*test+1))/6+(test*(test+1))/2)/2;
i=0;
while(sum>=10)
{
i++;
sum=sum/10;
}
printf("%.2fE%d\n",sum,i);
scanf("%lf",&test);
}
return 0;
}
posted @
2010-09-06 10:11 jince 阅读(473) |
评论 (0) |
编辑 收藏
有时候失去的总比得到的多！
Description
The Double Seventh Festival, on the 7th day of the 7th lunar month, is a traditional festival full of romance. On that day, the God of the Love came to the digital kingdom, and annunciated to the people:
Notification
Do you want to know who is your fere? You can find him or her by this means:
Please add all the factors of your ID-Card-Number, and you can find this is your fere's
ID-Card-Number.
The factors of a numer N is the numbers,they being small than the number N ,and can being divided exactly by the number N.
For example, the number 12 has the factors, such as 1,2,3,4,6.
Input
The fist line is the number T (1 <= T <= 500000), indicated the number of the test cases.
The next T lines, each line has one integer N( 1 <= N <= 500000), meaning the ID-Card-Number.
Output
For each test case, you should output the fere's ID-Card-Number on a line.
Sample Input
3
2
10
20
Sample Output
1
8
22
这个题目在我刚开始接触ACM的时候做出来最有成就的一个！求各因子之和！
代码如下：
#include<cstdio>
int main()
{
int i,j,n,m,sum;
scanf("%d",&n);
for(i=0;i<n;i++)
{
sum=0;
scanf("%d",&m);
for(j=1;j*j<=m;j++)
{
if(m%j==0)
{
sum=sum+j+m/j;
}
if(j*j==m)
sum-=j;
}
printf("%d\n",sum-m);
}
return 0;
}
posted @
2010-09-06 09:34 jince 阅读(1022) |
评论 (0) |
编辑 收藏
下午真的很想睡觉，可是上床，下床好几次了，都没睡着，焦虑啊！！可能像我这样刚毕业的人都会这样！工资好像还没发！我问他们，他们说其他人都发了。。。马上又要交房租了，我想对房东说，我已经打到你卡上了，你没收到吗？然后我就去露宿街头。。。我很勇敢，但是我不傻！
给定n个整数（可能为负）组成序列a1,a2,...an，求该序列的最大和子段！这个题目有很多解法！！！
一、穷举法
这种方法很容易想到，就不怎么说明了，直接上代码！
代码如下：
int MaxSum(int n,int *a,int &besti,int& bestj)
{
int sum=0;
int i,j;
for(i=1;i<=n;i++)
{
int thissum=0;
for(j=i;j<=n;j++)
{
thissum+=a[j];
if(thissum>sum)
{
sum=thissum;
besti=i;
bestj=j;
}
}
}
return sum;
}
二、二分法
将数组a[1..n]分成左右的两段a[1..n/2]和a[n/2+1...n]；最大和字段可能落在左子段，可能落在右子段，也可能落在中间，即一部分在左，一部分在右；对于前面两种情况可以直接递归求解，对于最后这种情况，只要从a[n/2]出发，分别累加左子段和得到一个最大值s1，右子段和得到一个最大值s2，s1+s2可得到一个最优值；然后取三者最优！！
代码如下：
int MaxSubSum(int *a,int left,int right)
{
int sum=0;
int j,i;
if(left==right) sum=a[left]>0?a[left]:0;
else
{
int center=(left+right)/2;
int leftsum=MaxSubSum(a,left,center);
int rightsum=MaxSubSum(a,center+1,right);
int s1=0;
int lefts=0;
for(i=center;i>=left;i--)
{
lefts+=a[i];
if(lefts>s1)
s1=lefts;
}
int s2=0;
int rights=0;
for(j=center+1;j<=right;j++)
{
rights+=a[j];
if(rights>s2)
s2=rights;
}
sum=s1+s2;
if(sum<leftsum) sum=leftsum;
if(sum<rightsum) sum=rightsum;
}
return sum;
}
其实这个算法先将n大的序列二分置大小为1的序列，然后回溯回去，回溯过程中一直取最优值，实现了信息填充和附带功能！
三、动态规划
这种算法最简单，效率也最高，但是不是很容易理解！好的东西常常很难去解释！
我个人是这么理解的，假设最大序列是从第一个数开始加的一个子序列，那么我们只要从第一个数一直加，取最大的那个值解释最优了！当然这只是假设，最大子序列的初始位置可能会在其他地方，这里就有一个舍弃和，和重新累加的问题，假设从1开始加我们得到一个正和，我们就舍弃（当然在这个过程中我们会一直比较最优值，并把它记录下来），重新累加，显然，无论后面累加得到一个正和或者负和我们都应该把前面那个舍弃的正和加进去；类似的当从1累加得到非正数时，我们就应该把它这段累加和舍弃，重新开始累加！
代码如下：
//求一维数组最大和子段 不考虑数组全为负的情况
int maxsum(int n,int *a)
{
int sum=0,b=0;
int i;
for(i=1;i<=n;i++)
{
if(b>0)
b+=a[i];
else
b=a[i];
if(b>sum) sum=b;
}
return sum;
}
最终其实会得到一幅以数列为轴的点图，最高那个就是最大和字段和！
posted @
2010-09-05 17:29 jince 阅读(564) |
评论 (2) |
编辑 收藏
问题描述：给定序列X={x1,x2,..xn}和Y={y1,y2...ym},求一个Z={z1,z2,..zk}序列是X,Y的最长公共子序列！！
书上描述的已经十分详细了，而且容易理解。通过定义c[i][j]用于记录Xi和Yi的最长公共子序列的长度，从而递推得到结果。
递推方程如下：
c[i][j]=0,i=0,j=0； c[i][j]=c[i-1][j-1]+1,xi=yj； c[i][j]=max(c[i-1][j],c[i][j-1]),xi!=yj；
（不知道怎么输出大括号，悲剧啊！）
代码如下：
#include<stdio.h>
void LCSLength(int m,int n,char *x,char *y,int c[][100],int b[][100])
{
int i,j;
for(i=1;i<=m;i++) c[i][0]=0; //当i==0或者j==0时，代表其中一个序列为空，c[i][j]当然为0
for(j=1;j<=n;j++) c[0][j]=0;
for(i=1;i<=m;i++) //二重循环
for(j=1;j<=n;j++)
{
if(x[i]==y[j])
{
c[i][j]=c[i-1][j-1]+1;
b[i][j]=1;
}
else
{
if(c[i-1][j]>=c[i][j-1])
{
c[i][j]=c[i-1][j];
b[i][j]=2;
}
else
{
c[i][j]=c[i][j-1];
b[i][j]=3;
}
}
}
}
void LCS(int i,int j,char x[],int b[][100]) //递归求得最长子序列
{
if(i==0||b==0)
return;
if(b[i][j]==1)
{
LCS(i-1,j-1,x,b);
printf("%c",x[i]);
}
else if(b[i][j]==2)
LCS(i-1,j,x,b);
else
LCS(i,j-1,x,b);
}
int main()
{
char x[100],y[100];
int i,j;
int c[100][100],b[100][100];
scanf("%s %s",x+1,y+1);
c[0][0]=0;
LCSLength(7,6,x,y,c,b);
for(i=0;i<8;i++)
{
for(j=0;j<7;j++)
{
printf("%d ",c[i][j]);
}
printf("\n");
}
LCS(7,6,x,b);
printf("\n");
return 0;
}
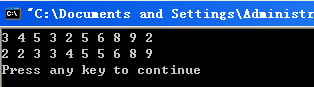
运行结果：
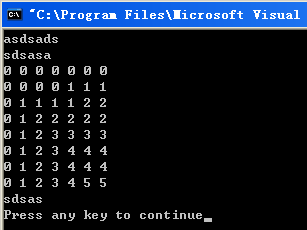
posted @
2010-09-04 23:17 jince 阅读(318) |
评论 (0) |
编辑 收藏
矩阵相乘问题描述：给定n个矩阵{A1，A2，...，An}，当然A1到An的任意段都是可乘的，求最小相乘次数。例如有三个矩阵维数分别为：10*100，100*2，2*5；若前两个相乘，再乘第三个，总的相乘次数=10*100*2+10*2*5=2100；若第二个与第三个先相乘，在乘第一个，总相乘次数=100*2*5+10*100*5=5100；显然，相乘次序会对计算量有很大影响，如果你在学线性代数的时候，写了一个矩阵相乘的程序，结果跑到同学那里演示的时候，半天没运行出来，那就尴尬了！！！
函数调用一般会要传参，这些参数都是非常有意义。这个题目属于动态规划，最重要的一点就是想到一个二维数组m[i][j]，代表矩阵i到矩阵j相乘的最优解，然后就是怎样给这个有意义的数组置数了，这种数组定义和数组置数若成，则我们要的答案就在m[1][n]中，代表矩阵1到矩阵n相乘的最优解。（如果你很饥渴的想解决这个问题，就直接看代码吧！！）有人可能会问，为什么会想到这种数组定义，主要有两个方面：一，学习（高效），看多了自然会想到给数组某种意义，培育一种思想；二、思考与分析，来的缓慢，但是凌驾与学习之上，也是学习的目的，是终极武器，也是基础武器。。。。
不扯了，回到主题，很明显如果只有一个矩阵，相乘次数为零；如果有两个，直接相乘，若第一个矩阵维数q*p，第二个矩阵维数p*r，相乘次数为q*p*r；三个矩阵相乘，为前两相乘，再乘第三个，和后两个先相乘，再乘第一个，取其优者；四个矩阵相乘，设第三个矩阵维数r*t，第四个矩阵t*k，维数min{前三个矩阵最优值+q*t*k，前两个矩阵最优+后两个矩阵最优+q*r*k，前一个矩阵最优+后三个矩阵最优+q*p*k}；然后。。。
有人可能会问：我可以算出前一个，前两个，前三个矩阵相乘的最优，但是我怎么算出后一个，后两个，后三个相乘的最优呢？
其实这个问题又回到了原点，这就是动态规划的妙处，显然我们先求出A1到An的任意段长度为2矩阵的最优（直接相乘），然后可以计算出任意段长度为3矩阵的最优；然后。。。然后我们就想了个m[i][j]出来，记录我们求的的结果；然后再写代码，尝试思想的准确性，当然我们更多的时候是站在先人的肩膀上做验证工作。。。
代码如下（参考教科书）：
#include<iostream>
using namespace std;
void chain(int *p,int n,int m[][7],int s[][7])//p维数数组，m最优乘次数组，s记录划分方案
{
int j;
for(int i=1;i<=n;i++)
m[i][i]=0;
for(int r=2;r<=n;r++)
{
for(i=1;i<=n-r+1;i++)
{
j=i+r-1;
m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];
s[i][j]=i;
for(int k=i+1;k<j;k++)
{
int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(t<m[i][j])
{
m[i][j]=t;
s[i][j]=k;
}
}
}
}
for(i=1;i<=n;i++) //我把它翻过来输出。。。
{
for(j=n;j>=i;j--)
{
cout<<m[i][j]<<' ';
}
cout<<endl;
}
}
void Traceback(int i,int j,int s[][7]) //输出相乘方案
{
if(i==j)
return;
Traceback(i,s[i][j],s);
Traceback(s[i][j]+1,j,s);
cout<<"Multiply A "<<i<<","<<s[i][j];
cout<<" and B "<<(s[i][j]+1)<<","<<j<<endl;
return;
}
int main()
{
int p[7],m[7][7],s[7][7],n;
while(scanf("%d",&n)!=EOF)
{
for(int i=0;i<=n;i++)
{
scanf("%d",&p[i]);
}
chain(p,n,m,s);
Traceback(1,6,s);
}
return 0;
}
/**//*
p52
测试数据：
6
30 35 15 5 10 20 25
*/
运行结果：
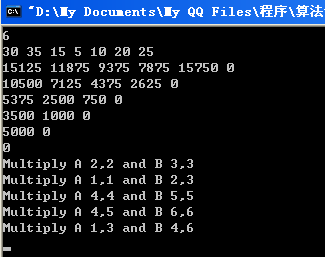
posted @
2010-09-04 11:53 jince 阅读(2520) |
评论 (0) |
编辑 收藏按照vector容器函数说明测了一下，一一应验！
代码如下：
#include<stdio.h>
#include<vector>
#include<iostream>
#include<algorithm>
#include<functional>
using namespace std;
bool cmp(const int &a,const int &b)
{
return a>b;
}
int main()
{
vector<int> v1;
v1.push_back( 0 );
v1.push_back( 1 );
v1.push_back( 2 );
v1.push_back( 3 );
vector<int> v2;
v2.push_back( 5 );
v2.push_back( 6 );
v2.push_back( 7 );
v2.push_back( 8 );
cout << "Before, v2 is: ";
for( vector<int>::size_type i = 0; i < v2.size(); i++ )
{
cout << v2[i] << " ";
}
cout << endl;
/**//* cout << "Before, v2 is: ";
for( vector<int>::iterator iter =v2.begin() ; iter < v2.end(); iter++ ) {
cout << *iter << " ";
}
cout << endl;//迭代器，相当于指针的概念。。*/
// v2.insert( v2.end(), v1.begin(), v1.end() );//在v2末尾插入v1
// v2.insert(v2.end(),3,'3'); //在v2末尾插入3个51
// swap(v1,v2);
// v1.swap(v2); //交换
// printf("%d\n",v2.at(2)); // 输出指定位置值
// sort(v2.begin(),v2.end(),cmp); //排序，一直没弄明白cmp
// sort(v2.begin(),v2.end(),greater<int>()); //递减排序
// sort(v2.begin(),v2.end(),less<int>()); //递增排序
// v2.assign(v1.begin(),v1.end());//拷贝v1到v2
// v2.erase(v2.end()-1,v2.end()); //删除容器元素，不包括第一个数
// v2.clear(); //清空
// v2.resize(2); //修改元素个数
cout << "After, v2 is: ";
for( vector<int>::size_type j = 0; j < v2.size(); j++ )
{
cout << v2[j] << " ";
}
return 0;
}
posted @
2010-09-03 13:52 jince 阅读(193) |
评论 (0) |
编辑 收藏
书上有一个用C++设计自己的输出/输入操作，涉及到运算符重载和流提取符重载，挺不错的！
代码如下：
COMPLEX.HPP文件
#include<iostream.h>
class COMPLEX {
public :
COMPLEX(double r=0,double i=0);
COMPLEX(const COMPLEX& other);
COMPLEX operator +(const COMPLEX& other);
COMPLEX operator -(const COMPLEX& other);
COMPLEX operator -();
COMPLEX operator =(const COMPLEX &other);
friend ostream& operator <<(ostream& stream,COMPLEX& obj);
friend istream& operator <<(istream& stream,COMPLEX& obj);
public :
double real,image;
};
COMPLEX.CPP文件
//COMPLEX.CPP文件
#include "COMPLEX.HPP" //将头文件包括进去,不能写成include<COMPLEX.CPP>。。。
COMPLEX::COMPLEX(double r,double i)
{
real=r;
image=i;
return ;
}
COMPLEX::COMPLEX(const COMPLEX& other)
{
real=other.real;
image=other.image;
return ;
}
COMPLEX COMPLEX::operator +(const COMPLEX& other) //运算符+重载 参数为COMPLEX类型，返回值为COMPLEX类型的引用，下同
{
COMPLEX temp;
temp.real=real+other.real;
temp.image=image+other.image;
return temp;
}
COMPLEX COMPLEX::operator -(const COMPLEX& other)
{
COMPLEX temp;
temp.real=real-other.real;
temp.image=image-other.image;
return temp;
}
COMPLEX COMPLEX::operator =(const COMPLEX& other)
{
real=other.real;
image=other.image;
return *this;
}
ostream& operator<<(ostream& stream,COMPLEX& obj) //流提取符重载有两个参数，第一个参数出现在<<操作符左侧，为ostream引用，第二个出现在操作符<<右侧，为COMPLEX引用，返回值是一个ostream的对象引用，下同
{
stream<<obj.real;
if(obj.image>0) stream<<"+"<<obj.image<<"i";
else if(obj.image<0) stream<<obj.image<<"i";
return stream;
}
istream& operator>>(istream& stream,COMPLEX& obj)
{
cout<<"Input real part:";
stream>>obj.real;
cout<<"input image part:";
stream>>obj.image;
return stream;
}
int main()
{
COMPLEX c1,c2;
cout<<"Input the first complex number c1:"<<endl;
cin>>c1;
cout<<"Input the second compex number c2:"<<endl;
cin>>c2;
cout<<"c1 is"<<c1<<endl;
cout<<"c2 is"<<c2<<endl;
cout<<"c1+c2 is "<<c2+c1<<endl;
cout<<"c1-c2 is "<<c1-c2<<endl;
//操作符原功能任存在
int a=50,b=10;
cout<<"A="<<a<<"\tB"<<b<<endl;
cout<<"A+B is "<<a+b<<endl;
cout<<"A-B is "<<a-b<<endl;
a=-b;
cout<<"A=-B,A="<<a<<"\tB"<<b<<endl;
a=b;
cout<<"A=B,A="<<a<<"\tB"<<b<<endl;
return 0;
}
输出结果：
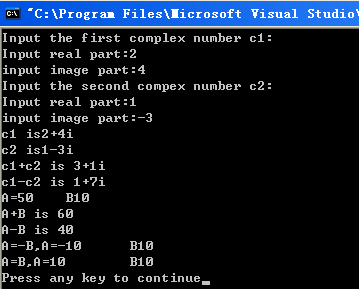
posted @
2010-09-02 22:08 jince 阅读(494) |
评论 (0) |
编辑 收藏
网上搜了下棋盘覆盖，结果看到了哈佛校训。。。。
棋盘覆盖是在一个2^k*2^k的棋盘中存在一个特殊格子，现要求用L型覆盖整个棋盘（除特殊格子），问如何覆盖这个棋盘？
在学校的时候，这题目是只看懂了解题思路，代码没仔细看过，现在在重新看的时候，感觉其实也不是那么难看懂！
先看解题思路截图：
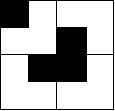
看到这个截图你会有何感想呢？其实不就是个分治嘛！将一个2^k*2^k棋盘分割成4个2^(k-1)*2^(k-1),然后问题回到原点，在2^(k-1)*2^(k-1)棋盘中有一个特殊格子，求其用L型骨牌覆盖方法！
代码如下：
#include<stdio.h>
int Board[64][64];
int tile;
void ChessBoard(int tr,int tc,int dr,int dc,int size)//tr为棋盘左上角方格行号，tc为棋盘左上角列号，dr为特殊格行号，dc为特殊格列号，size=2^k，棋盘规格
{
if(size==1) //当分到只剩下一个格子的时候,该格就是本次递归特殊格
return ;
int t=++tile;
int s=size/2;
if(dr<tr+s&&dc<tc+s) //特殊格在棋盘左上角
ChessBoard(tr,tc,dr,dc,s);
else
{
Board[tr+s-1][tc+s-1]=t;
ChessBoard(tr,tc,tr+s-1,tc+s-1,s);
}
if(dr<tr+s&&dc>=tc+s) //特殊格在棋盘右上角
ChessBoard(tr,tc+s,dr,dc,s);
else
{
Board[tr+s-1][tc+s]=t;
ChessBoard(tr,tc+s,tc+s-1,tc+s,s);
}
if(dr>=tr+s&&dc<tc+s) //特殊格在棋盘左下角
ChessBoard(tr+s,tc,dr,dc,s);
else
{
Board[tr+s][tc+s-1]=t;
ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
}
if(dr>=tr+s&&dc>=tc+s) //特殊格在棋盘右下角
ChessBoard(tr+s,tc+s,dr,dc,s);
else
{
Board[tr+s][tc+s]=t;
ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
}
}
int main()
{
int i,j,k,l;
/**//*for(k=0;k<64;k++)
for(l=0;l<64;l++)
{ */
Board[2][1]=0;
tile=0;
ChessBoard(0,0,2,1,4);
for(i=0;i<4;i++)
{
for(j=0;j<4;j++)
{
printf("%d ",Board[i][j]);
}
printf("\n");
}
printf("\n");
// }
return 0;
}
输出结果：
哈佛校训：
此刻打盹，你将做梦，此刻学习，你将圆梦！ 受教！！
posted @
2010-09-02 13:59 jince 阅读(422) |
评论 (0) |
编辑 收藏
公司不发工资了。。。。
快速排序算法是基于分治算法的一种排序。主要思想分成两步（从小到大排序）：
（1）分解，取出排序数列中一个数字，将数分成三段，左边段数列数值大于等于取出数，右边段数列值小于等于取出数，中间是取出数；
（2）递归求解；
第一步其实是根据分治算法的基本思想，将一个规模为n的问题分成3个规模较小的问题，其中规模为1的在这次运算后，就是最后结果中的位置了；
第二步其实是将规模较小的另两个数列，继续分解下去，其中每一次分解都会确定一个数在最后结果中的位置，
在这样的思想下，该程序设计最关键的一种操作就是怎样把数组分解成左边段数列数值大于等于取出数，右边段数列值小于等于取出数；
书上的代码如下：
#include<iostream>
#include<algorithm>
using namespace std;
template <class Type>
void QuickSort(Type a[],int p,int r)
{
if(p<r)
{
int q=Partition(a,p,r); //分解
QuickSort(a,p,q-1); //左半段排序
QuickSort(a,q+1,r); //有半段排序
}
}
void Swap(int &a,int &b) //交换
{
int c;
c=a;
a=b;
b=c;
}
int Partition(int a[],int p,int r) //分解
{
int i=p,j=r+1; //为啥i=p,j=r+1呢？
int x=a[p]; //因为取第一个数为参考值
while(1) //死循环
{
while(a[++i]<x&&i<r); //一个从左边找比x大的数
while(a[--j]>x); //一个从右边找比x小的数
if(i>=j) //死循环跳出条件，为什么是i>=j呢？i>=j意味着j左边数列值都小于x（包括j），右边数列值都大于x了！
break;
Swap(a[i],a[j]); //没跳出死循环，就应该交换
}
a[p]=a[j];
a[j]=x; //交换p与j位置上的值，因为a[j]<=x！！到这里p位置上的数，位置就确定下来了！
return j; //返回位置值，为另两端提供参数！
}
int main()
{
int i;
int a[10]={3,4,5,3,2,5,6,8,9,2};
for(i=0;i<10;i++)
printf("%d ",a[i]);
printf("\n");
QuickSort(a,0,9);
for(i=0;i<10;i++)
printf("%d ",a[i]);
printf("\n");
return 0;
}
输出结果：
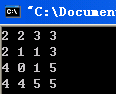
特殊情况下：如果选取的a[p]是数列最小值，Partition(a,p,r)返回p，a[p]值不变！我测试了一下，是期望结果。。。
网上还有快速排序视屏，巨好玩！http://v.youku.com/v_show/id_XMTg1MjIwMDY0.html
posted @
2010-09-01 16:14 jince 阅读(373) |
评论 (1) |
编辑 收藏
以前做过这么一个题目，在我们学校ACM网上，找了很久没找到，郁闷！网上走了一遭，基本和书上介绍的差不多，虽然做过但是重新去看思路的时候还是比较慢！！！我再写一下，加深影响！
整数划分就是将一个正整数表示成一系列正整数之和，问有多少种不同划分方案！
例如整数6可以划分成一下11中方案：
6
5 + 1
4 + 2, 4 + 1 + 1
3 + 3, 3 + 2 + 1, 3 + 1 + 1 + 1
2 + 2 + 2, 2 + 2 + 1 + 1, 2 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1
如果你是编程好手看到这样的排列，可能一下子就能想到一种解题思路了！感慨，算法就是在培养解决问题的思路！！言归正传！先介绍下书上的思路：
一、p(n,m)含义：在正整数n的所有不同划分中，最大加数不大于m的划分数（m<=n；m,n>=1）！求整数6有几种划分时，既求p(6,6)。。。
二、函数递归关系：
1、n<1||m<1，return 0；
2、n==1||m==1，p(n,m)=1；
3、n<m，p(n,m)=p(n,n)；例如：p(6,10)=p(6,6)
4、n>m，p(n,m)=p(n,m-1)+p(n-m,m)；例如：p(6,5)=p(6,4)+p(2,4)； p(6,2)=p(6,1)+p(4,2)；
（这个等式是关键）
代码如下
#include<cstdio>
int q(int n,int m)
{
if((n<1)||(m<1)) return 0;
if(n==1||m==1) return 1;
if(n<m) return q(n,n);
if(n==m) return q(n,m-1)+1;
return q(n,m-1)+q(n-m,m);
}
int main()
{
printf("%d\n", q(6,6));
return 0;
}
写完书上的解题思路，我突然发现前面我想到的一种解题思路错了！！不过这种递归算法运行效率低，计算整数35分解方案数的时候，计算速度很慢（大概两秒出现答案14930352），40的时候更慢了- -，我想用二维数组填表的方式应该会快一点！！有更好算法的可以留言！！随时候教~~
posted @
2010-08-31 15:25 jince 阅读(2422) |
评论 (2) |
编辑 收藏