包含平移的线性变换称作仿射变换,3D中的仿射变换不能用 3 x 3 矩阵表达,必须使用4
x 4矩阵。
一般来说,变换物体相当于以相反的量变换描述这个物体的坐标系。当有多个变换时,则需要以相反的顺序变换相反的量。例如,将物体顺时针旋转20度,扩大200%,等价于将坐标系缩小200%,再逆时针旋转20度。
2D中的旋转
在2D环境中,物体只能绕某个点旋转,因为现在暂不考虑平移。这里我们进一步限制物体,使其只绕原点旋转。2D中绕原点的旋转只有一个参数,角度θ,它描述了旋转量。逆时针旋转经常(不是必须)被认为是正方向,顺时针方向是负方向。图8.5展示了基向量p,q绕原点旋转,得到新的基向量p',q'。
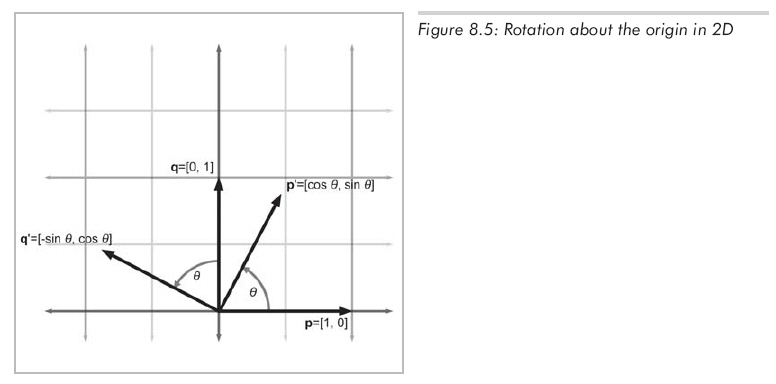
现在我们知道了旋转后基向量的值,就可以以公式8.1的形式构造矩阵如下:
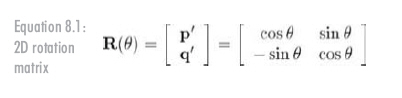
3D中绕坐标轴的旋转
在3D场景中,绕轴旋转而不是点(此时轴指的是旋转所绕的直线,不一定是笛卡尔坐标轴x,y,z)。再次声明,这里暂不考虑平移,所以只讨论旋转轴穿过原点的情况。
绕轴旋转角度θ时,必须知道哪个方向被认为“正”,哪个方向被认为“负”,左手坐标系中定义此方向的规则为左手法则。首先,要明确旋转轴指向哪个方向。当然,旋转轴在理论上是无限延伸的,但我们还是要认为它有正端点和负端点。与笛卡尔坐标轴定义坐标系相同,左手法则是这样的:伸出左手,大拇指向上,其余手指弯曲。大拇指指向旋转轴的正方向,此时,四指弯曲的方向就是旋转的正方向。如图8.6所示。
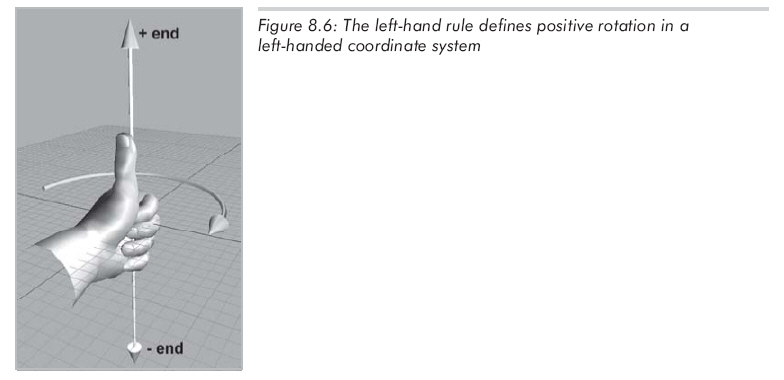
如果用的是右手坐标系,也有类似的法则,不过是用右手代替左手,如图8.7所示:
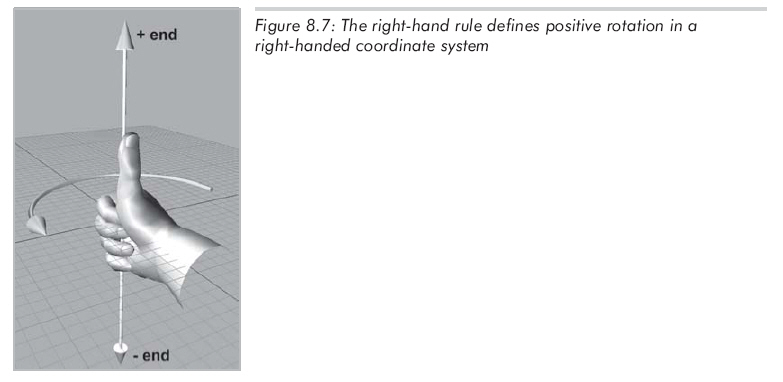
图8.8显示了另一种正方向的定义:
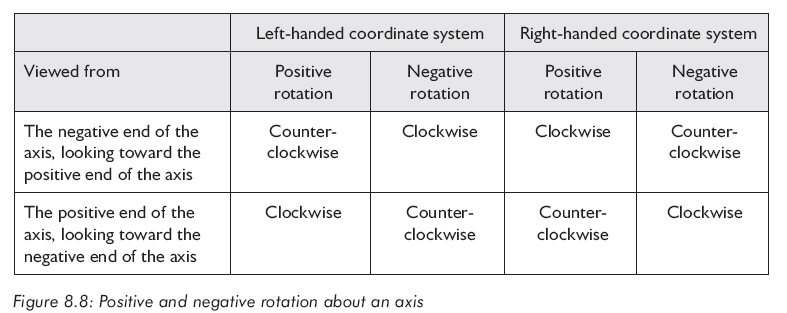
最为常见的旋转是绕某坐标轴的简单旋转,让我们从绕x轴旋转开始,如图8.9所示:

求出旋转后的基向量,可以得到矩阵,见公式8.2。
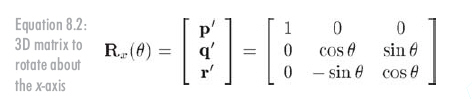
Rotation about the y-axis is similar:
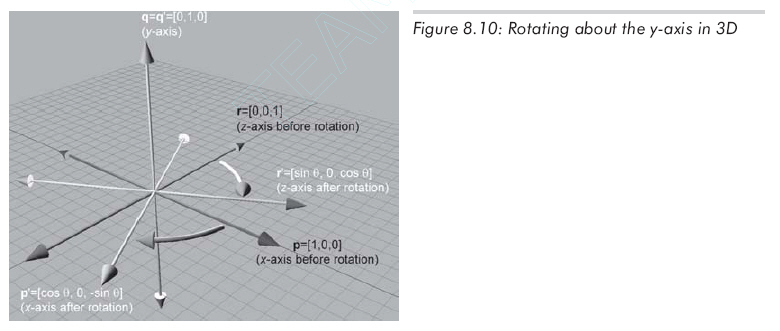
The matrix to rotate about the y-axis:
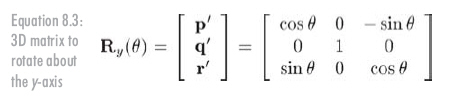
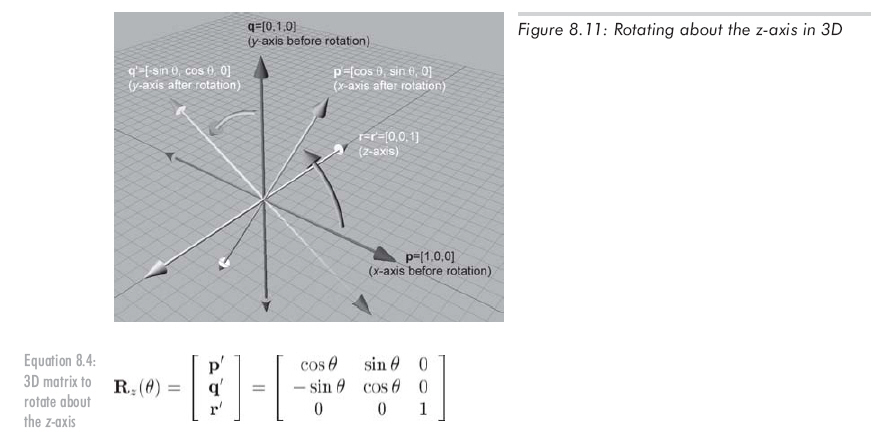
Finally, rotating about the z-axis:
3D中绕任意轴的旋转
当然也能绕3D中的任意轴旋转。因为这里不考虑平移,可以假设旋转轴通过原点,这种旋转比绕坐标轴的旋转更复杂也更少见。用单位向量n描述旋转轴,和前面一样用θ描述旋转量。
让我们导出绕轴n旋转角度θ的矩阵,也就是说,我们想得到满足下面条件的矩阵 R(n,
θ):
vR(n, θ) = v'
v'是向量v绕轴n旋转后的向量。让我们看看能否用v,n和θ表示v'。我们的想法是在垂直于n的平面中解决这个问题,那么这就转换为了一个简单的2D问题。为了做到这一点,将v分解为两个分量:v||和v⊥,分别平行于n和垂直于n,并有v
= v|| + v⊥。因为v||平行于n,所以绕n旋转不会影响它。故只要计算出v⊥绕n旋转后的
v⊥',就能得到 v' =v||
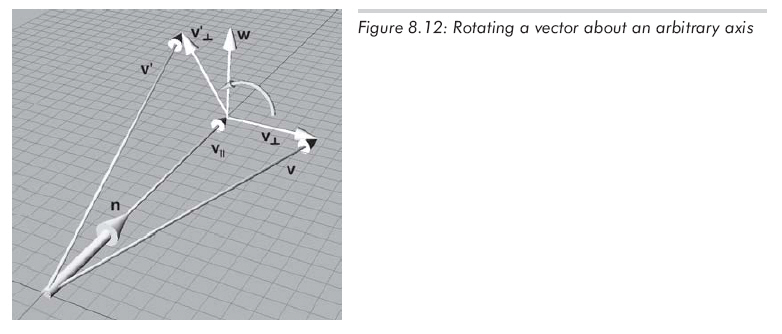
+ v⊥'。为了计算v⊥',我们构造向量v||
,v⊥和临时向量w,如图8.12所示:
 ’
’
上图展示了以下向量:
(1)v|| 是v平行于n的分量,另一种说法就是v||
是v在n上的投影,用(v.n)n计算。
(2)v⊥是v垂直于n的分量,因为
v = v|| + v⊥,所以
v⊥ = v - v||。v⊥是v投影到垂直于n的平面上的结果。
(3)w是同时垂直于v||和v⊥的向量,它的长度和v⊥的相同。w和v⊥同在垂直于n的平面中,w是v⊥绕n旋转90度的结果,由n
x v⊥可以得到。
现在,v'垂直于n的分量可以表示为:


