另一种描述方位的常用方法是欧拉角,这项技术以著名的数学家Leonhard Euler(1707 -
1783)的名字命名,他证明了角位移序列等价于单个角位移。
什么是欧拉角
欧拉角的基本思想是将角位移分解为绕三个互相垂直轴的三个旋转组成的序列。这听起来很复杂,其实它是非常直观的(事实上,易于使用正是它的主要优点之一)。之所以有"角位移"的说法正是因为欧拉角能用来描述任意旋转。
欧拉角将方位分解为绕三个互相垂直轴的旋转,那么是哪三个轴?按什么顺序?其实,任意三个轴和任意顺序都可以,但最有意义的是使用笛卡尔坐标系并按一定顺序所组成的旋转序列。最常用的约定是所谓的"heading
- pitch - bank"约定。在这个系统中,一个方位被定义为一个heading角,一个pitch角,一个bank角。它的基本思想是让物体开始于"标准"方位
--- 就是物体坐标轴和惯性坐标轴对齐。在标准方位上,让物体作heading、pitch、bank旋转,最后物体到达我们想要描述的方位。
如图10.4所示,此时物体坐标系和惯性坐标系重合,heading为绕y轴的旋转量,向右旋转为正(如果从上面看,旋转正方向就是顺时针方向)。
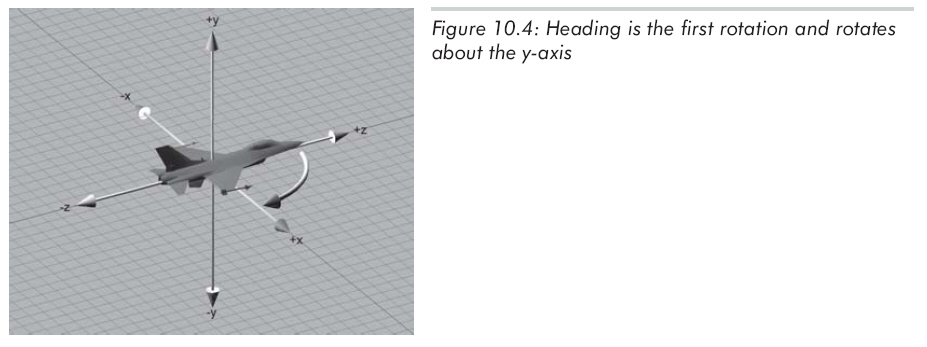
经过heading旋转后,pitch为绕x轴的旋转量,注意是物体坐标系的x轴,不是原惯性坐标系的x轴。依然遵守左手法则,向下旋转为正,如图10.5所示:
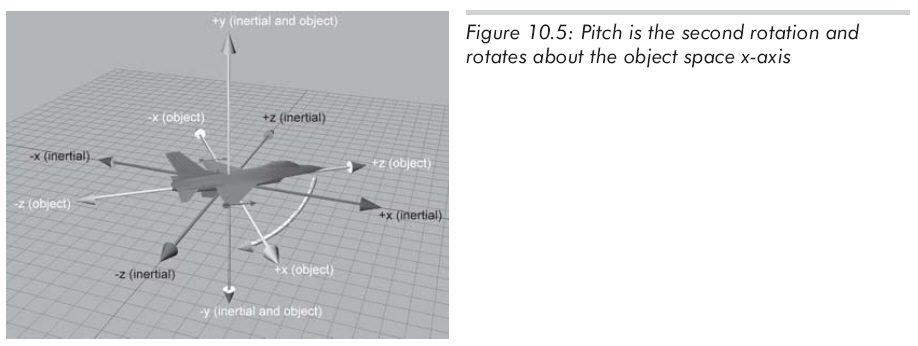
最后,经过了heading和pitch,bank为绕z轴的旋转量。再次提醒,是物体坐标系的z轴,不是原惯性坐标系的z轴。依据左手法则,从原点向+z看,逆时针方向为正。如图10.6所示:
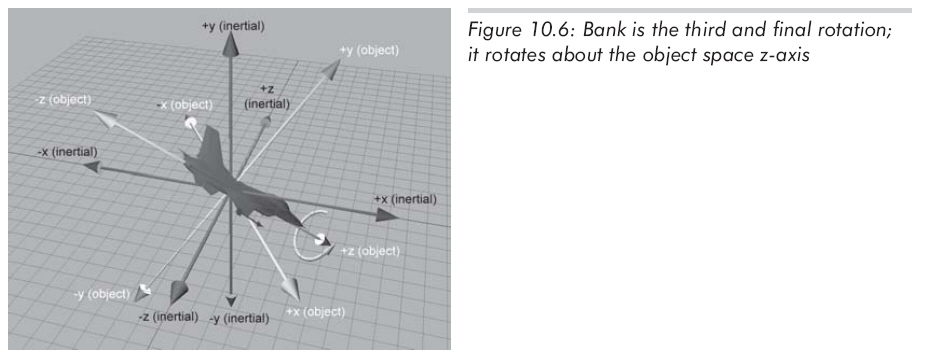
记住,当我们说旋转的顺序是heading-pitch-bank时,是指从惯性坐标系到物体坐标系。如果从物体坐标系变换到惯性坐标系,旋转的顺序就是相反的。"heading-pitch-bank"也叫作"roll-pitch-yaw",roll类似于bank,yaw类似于heading(事实上,yaw并不严格等于heading)。注意,在roll-pitch-yaw系统中,角度的命名顺序与从物体坐标系到惯性坐标系的旋转顺序一致的。
关于欧拉角的其他约定
heading-pitch-bank系统不是唯一的欧拉角系统。绕任意三个互相垂直轴的任意旋转都能定义一个方位,所以多种选择导致了欧拉角约定的多样性:
(1)heading-pitch-bank系统有多个名称。当然,不同的名字并不代表不同的约定,这其实并不重要。一组常用的术语是roll-pitch-yaw,其中的roll等价于bank,yaw基本上等价于heading。注意,它的顺序和heading-pitch-bank的顺序相反,这只是语义上的。它定义了向量从物体坐标系变换到惯性坐标系的旋转顺序。(事实上,yaw和heading还是有技术上的差别,yaw是绕物体坐标系y轴的旋转,heading是绕惯性坐标系y轴的旋转。因为这里的旋转是在物体坐标系y轴和惯性坐标系y轴重合时进行的,所以这个区别并不重要。)
(2)任意三个轴都能作为旋转轴,不一定必须是笛卡尔轴,但使用笛卡尔轴最有意义。
(3)决定每个旋转的正方向时不一定必须遵守左手或右手法则。例如,完全可以定义pitch的正方向是向上的,并且这种定义方法非常常见。
(4)也是最重要的,旋转可以以不同的顺序进行。顺序并不重要,任何系统都能用来定义一个方位,但heading-pitch-bank顺序最为实用。heading度量绕竖直轴的旋转,它之所以有意义主要是因为我们所在的环境经常有某种形式的"地面"。一般来讲绕惯性坐标系的x或z轴的旋转没有什么意义。heading-pitch-bank顺序下的另外两个角的意义是:pitch度量水平方向的倾角,bank度量的是绕z轴的旋转量。
欧拉角的优点
欧拉角仅使用三个数来表达方位,并且这三个数都是角度。这两个特点使欧拉角具有其他形式所没有的优点:
(1)欧拉角对我们来说很容易使用。它比矩阵和四元数简单得多,这可能是因为欧拉角中的数都是角度,符合人们思考方位的方式。如果我们选择了与所要处理的情况最符合的约定,那么就能直接描述出最重要的角度,例如,用heading-pitch-bank系统就能直接地描述出偏差角度。便于使用是其最大的优点,当需要显示方位或用键盘输入方位时,欧拉角是唯一的选择。
(2)最简洁的表达方式。欧拉角用三个数来表达方位。在3D中,表达方位不能少于三个数,如果要考虑内存的因素,欧拉角是最合适的描述方位的方法。
(3)任意三个数都是合法的。取任意三个数,它们都能构成合法的欧拉角,而且可以把它看成一个对方位的描述。从另一方面说,没有"不合法"的欧拉角。当然数值可能不对,但至少它们是合法的。可矩阵和四元数就不一定是这样了。
欧拉角的缺点
用欧拉角表达方位时的缺点主要有:
(1)给定方位的表达方式不唯一。
(2)两个角度间求插值非常困难。
让我们仔细讨论这些问题。第一个问题是对于一个给定方位,存在多个欧拉角可以描述它。这称作别名问题,有时候会引起麻烦。因为这个原因,连一些基本的问题(如"两组欧拉角代表的角位移相同吗?")都很难回答。
第一种,在将一个角度加上360度的倍数时,我们就会遇到形式最简单的别名问题。显然,加上360度并不会改变方位,尽管它的数值改变了。
第二种,更加麻烦的别名问题是由三个角度不互相独立而导致的。例如,pitch135度等价于heading180度,pitch45度,然后bank180度。为了保证任意方位都只有独一无二的表示,必须限制角度的范围。一种常用的技术是将heading和bank限制在+180度到-180度之间,pitch限制在+90度到-90度之间。这就建立了欧拉角的一个"限制范围"。对于任意方位,仅存在一个限制欧拉角能代表这个方位(事实上,还有一个违反唯一性的现象需要处理。)
欧拉角最著名的别名问题是这样的:先heading45度再pitch90度,这与先pitch90度再bank45度是等价的。事实上,一旦选择+(-)90度为pitch角,就被限制在只能绕竖直轴旋转。这种现象,角度为+(-)90度的第二次旋转使得第一次和第三次旋转的旋转轴相同,称作万向锁。为了消除限制欧拉角的这种别名现象,规定万向锁情况下由heading完成绕竖直轴的全部旋转。换句话说,在限制欧拉角中,如果pitch为+(-)90度,则bank为0。
如果是为了描述方位,特别是在使用了限制欧拉角的情况下,别名是不会造成太大的问题的。现在来看两个方位A和B间求插值的问题,也就是说,给定参数t,0
≤ t ≤ 1,计算临时方位C,当t从0变化到1时,C也平滑地从A变化到B。
这个问题的简单解法是分别对三个角度作标准线性插值,公式如下:
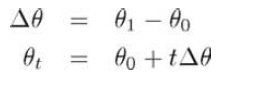
但这里面有很多问题。
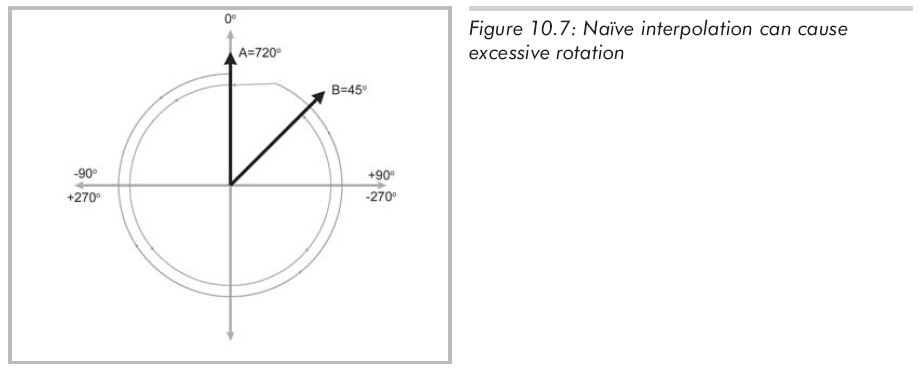
第一,如果没有使用限制欧拉角,将得到很大的角度差。例如,方位A的heading为720度,方位B的heading为45度,720
= 360 x 2,也就是0度。所以heading值只相差45度,但简单的插值会在错误的方向上绕将近两周。如图10.7所示:
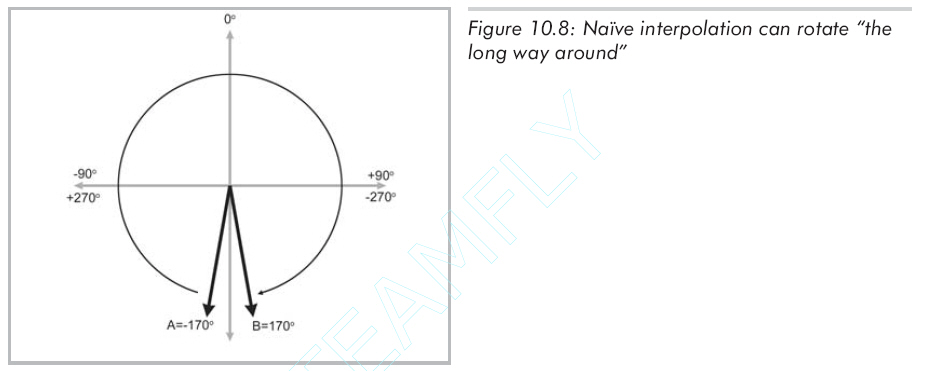
解决问题的方法是使用限制欧拉角,然而,即使是限制欧拉角也不能完全解决问题。插值的第二个问题是由旋转角度的周期性引起的。设A的heading为-170度,B的heading为170度。这些值在heading的限制范围内,都在-180度到180度之间。这两个值只相差20度,但插值操作又一次发生了错误,旋转是沿 "长弧"绕了340度而不是更短的20度,如图10.8所示:
解决这类问题的方法是将插值的"差"角度折到-180度到180度之间,以找到最短弧。
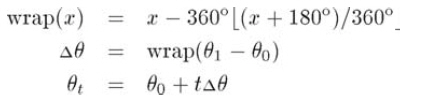
即使使用了这两个角度限制,欧拉角插值仍然可能碰到万向锁的问题,它在大多数情况下会产生抖动、路径错误等现象,物体会突然飘起来像是"挂"在某个地方。根本问题是插值过程中角速度不是恒定的。
欧拉角插值的前两个问题虽然烦人,但并不是不可克服的。限制欧拉角和将角度差限制在一定范围内提供了简单的解决方法。而对于万向锁,非常不幸,它非常令人讨厌,是一个底层的问题。你可能会考虑重新规划旋转,发明一种不会遭遇这些问题的系统。不幸的是,这不可能。这是一个用3个数表达3D方位的方法与生俱来的问题。我们可以改变问题,但不能消灭它们。任何使用三个数来表达3D方位的系统,若能保证空间的唯一性,就都会遇到这些问题,如万向锁。