天行健 君子当自强而不息

从四元数转换到矩阵

为了将角位移从四元数转换到矩阵形式，可以利用旋转矩阵，它能计算绕任意轴的旋转：

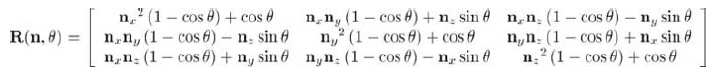
这个矩阵是用n和θ表示的，但四元数的分量是：

w = cos(θ/2)

x = n_x sin(θ/2)

y = n_y sin(θ/2)

z = n_z sin(θ/2)

让我们看看能否将矩阵变形以代入w、x、y、z，矩阵的9个元素都必须这样做。幸运的是，这个矩阵的结构非常好，一旦解出对角线上的一个元素，其他元素就能用同样的方法求出。同样，非对角线元素之间也是彼此类似的。

考虑矩阵对角线上的元素，我们将完整地解出m₁₁，m₂₂和m₃₃解法与之类似：

m₁₁ = n_x²(1 - cosθ) + cosθ

我们将从上式的变形开始，变形方法看起来像是在绕圈子，但你马上就能理解这样做的目的：

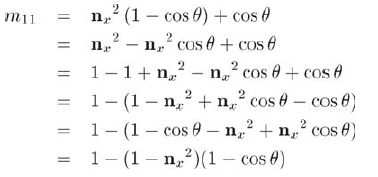
现在需要消去cosθ项，而代之以包含cosθ/2或sinθ/2的项，因为四元数的元素都是用它们表示的，像以前那样，设α=θ/2，先用α写出cos的倍角公式，再代入θ:

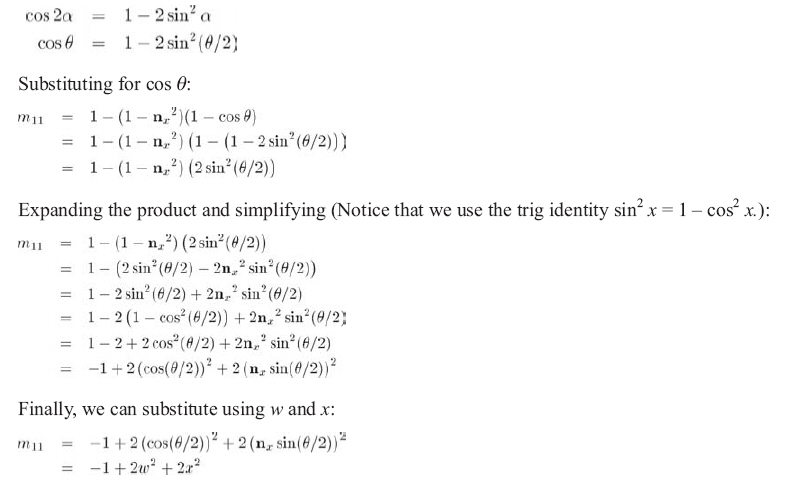
上式是正确的，但它和其他的标准形式不同，即:

m₁₁ = 1 - 2y² - 2z²

实际上，还有其他的形式存在。最著名的一个形式是m₁₁ = w² + x² - y²- z²，因为w² + x² + y² + z² = 1，所以这三种形式是等价的。现在回过头来看看能不能直接导出其他标准形式，第一步，n是单位向量，n_x²+n_y^{2 +} n_z² = 1，则1 - n_x² = n_y^{2 +} n_z²。

m₁₁ = 1 - (1 - n_x²)(2sin²(θ/2))

       = 1 - (n_y^{2 +}n_z²)(2sin²(θ/2))

       = 1 - 2n_y²sin²(θ/2) - 2n_z²sin²(θ/2)

       = 1 - 2y² - 2z²

元素m₂₂和m₃₃可以用同样的方法求得。

让我们来看看非对角线元素，它们比对角线元素简单一些，以m₁₂为例子：

m₁₂ = n_xn_y(1 - cosθ) + n_zsinθ

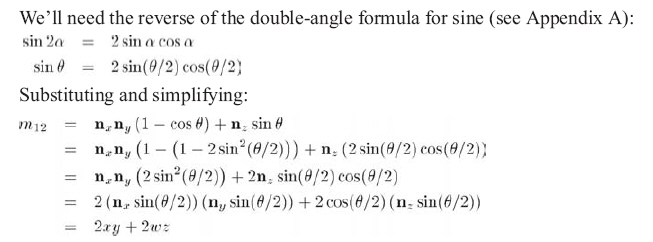
其他非对角线元素可用同样的方法导出。

最后，给出从四元素构造的完整旋转矩阵，如公式10.23所示：

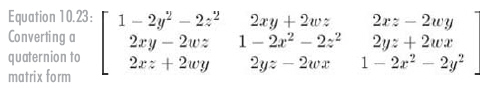
从矩阵转换到四元数

为了从旋转矩阵中抽出相应的四元数，可以直接利用公式 10.23，检查对角线元素的和（也称作矩阵的轨迹）得到：

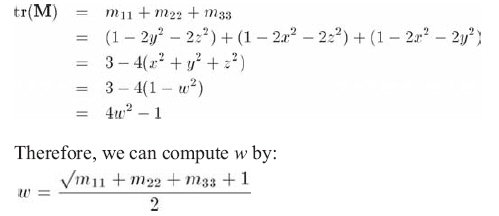
通过使轨迹中三个元素中的两个为负，可以用类似的方法求得其他三个元素:

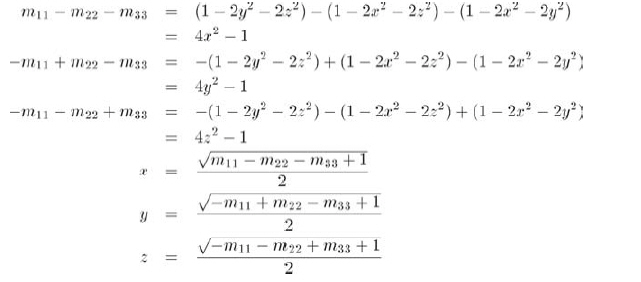
不幸的是，这种方法并不总是能正确工作，因为平方根的结果总是正值。（更加准确地说，没有选择正根还是负根的依据。）但是，q和-q代表相同的方位，我们能任意选择用非负根作为4个分量中的一个并仍能得到正确的四元数，只是不能对四元数的所有4个数都用这种方法。

另一个技巧是检查相对于对角线的对称位置上元素的和与差：

那么应选用四种方法中的哪个呢？似乎最简单的策略是总是先计算同一个分量，如w，然后再计算x、y、z。这伴随着问题，如果w=0，除法就没有定义；如果w非常小，将会出现数值不稳定。Shoemake建议先判断w、x、y、z中哪个最大（不用做平方根运算），根据上面的表，用矩阵对角线计算该元素，再用它计算其他三个。

下面的代码用一种非常直接的方式实现了这个方法。