新建网页 1
在3D中,平面是到两个点的距离相等的点的集合。平面完全是平的,没有厚度,且无限延伸。
平面方程 ---- 隐式定义
可以用类似于定义直线的方法来定义平面,平面的隐式定义由所有满足平面方程的点p=(x, y, z)给出,平面方程的两种记法如公式12.11所示:
ax + by + cz = d
p . n = d
公式12.11 平面方程
注意第二种形式中,n = [a, b, c]。一旦知道n,就能用任意已知的平面上的点来计算d。
向量n也称作平面的法向量,因为它垂直于平面。让我们来验证它,设p和q都在平面上,满足平面方程。将p、q代入式12.11,即有:
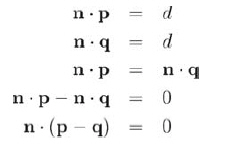
最后一行点乘的几何意义就是n垂直于从q到p的向量,这对于平面上的任意p、q点都是成立的,因此n垂直于平面上的任意向量。
我们还假设平面有"正面"和"反面"。一般来说,n指向的方向是平面的正面(front side)。即从n的头向尾看,我们看见的是正面,如图12.13所示:
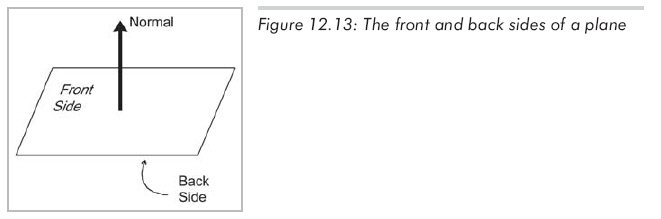
将n限制为单位长度并不会失去一般性,而且通常会给计算带来方便。
用三个点定义
另一种定义平面的方法是给出平面上不共线的三个点,也就是说,这三个点不在一条直线上。(如果三个点在一条直线上,就存在无数多个平面包含这条直线,这样也就无法说明我们指的是哪个平面了。)
让我们通过平面上的三个点p1、p2和p3来计算n和d。先计算n,n指向什么方向呢?左手坐标系中的惯例是:当从平面的正面看时,p1、p2和p3以顺时针方向列出。(右手坐标系中,经常假设这些点以逆时针方向列出,这样不管使用哪种坐标系公式,结果都是相同的。)
图12.14展示了使用平面上的三个点计算平面的法线向量的情况。
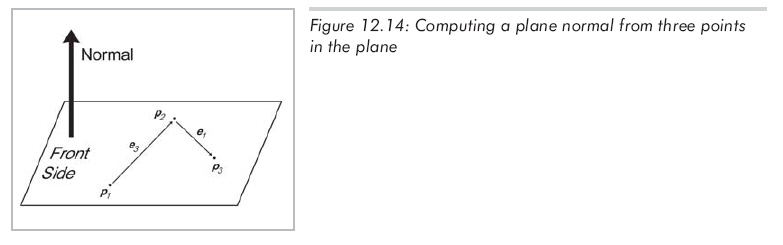
我们按顺时针方向构造两个向量(如图12.14所示),"e"代表"边(edge)"向量,因为这个公式经常用来计算三角形代表的平面。这两个向量叉乘的结果就是n,但可能不是单位向量,但我们可以单位化n,以上所有过程用公式12.12来简介地概括:
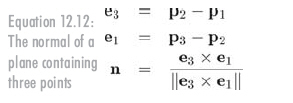
注意,如果这些点共线,则e3与e1平行。这样叉乘为0,不能单位化。这个数学上的特例与物理特例相吻合:共线点不能唯一地定义一个平面。
现在知道了n,剩下的就是求d,可以由某个点与n点乘获得。
多于三个点的"最佳"平面
有时,我们希望从一组三个以上的点集求出平面方程,这种点集最常见的例子就是多边形顶点。在这种情况下,这些顶点绕多边形顺指针地列出。(顺序很重要,因为要依据它决定哪边是"正面"哪边是"反面"。)
一种糟糕的方式是任选三个连续的点并用这三个点计算平面方程。毕竟所选的三个点可能共线,或接近共线。因为数值精度的问题,这将非常糟糕。或者,多边形可能是凹的,所选的点恰好在凹处,从而构成了逆时针(将导致法向量方向错误)。又或者,多边形上的顶点可能不是共面的,这可能是由数值上的不精确,或错误的生成多边形的方法所引起的。我们真正想要的是从点集中求出"最佳"平面的方法,该平面综合考虑了所有的点。设给定n个点:

如果我们限制n必须为单位向量,则这个向量必须单位化。
求和符号能使公式12.13更简洁些,设pn+1 = p1,则有:
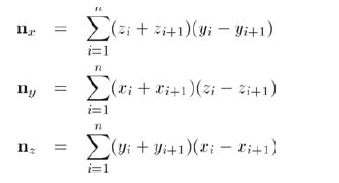
如下代码展示了怎样从点集中求出最佳法向量:
Listing 12.2: Computing the best-fit plane normal for a set of points
Vector3 computeBestFitNormal(const Vector3 v[], int n)
{
// Zero out sum
Vector3 result = kZeroVector;
// Start with the "previous" vertex as the last one.
// This avoids an if-statement in the loop
const Vector3 *p = &v[n–1];
// Iterate through the vertices
for (int i = 0 ; i < n ; ++i)
{
// Get shortcut to the "current" vertex
const Vector3 *c = &v[i];
// Add in edge vector products appropriately
result.x += (p–>z + c–>z) * (p–>y – c–>y);
result.y += (p–>x + c–>x) * (p–>z – c–>z);
result.z += (p–>y + c–>y) * (p–>x – c–>x);
// Next vertex, please
p = c;
}
// Normalize the result and return it
result.normalize();
return result;
}
最佳d值为每个点对应的d的平均值:
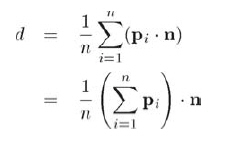
点到平面的距离
设想一个平面和一个不在平面上的点q,平面上存在一个点p,它到q的距离最短。很明显,从p到q的向量垂直于平面,且形式为an。如图12.15所示:

假设n为单位向量,那么p到q的距离(也就是q到平面的距离)就是a了。(如果q在平面的反面,这个距离为负。)令人惊奇的是,不用知道p的位置就能计算出a。让我们回顾q的原定义,并做一些向量计算以消掉p,如公式12.14所示: