新建网页 1
重心坐标空间
虽然我们经常在3D中使用三角形,但三角形的表面是一个平面,它天生是一个2D物体。在3D中任意朝向的三角形表面上移动是一件令人烦恼的事,最好是有一个坐标空间与三角形表面相关联且独立于三角形所在的3D坐标空间,重心坐标空间正是这样的坐标空间。
三角形所在平面的任意点都能表示为顶点的加权平均值,这个权就称作重心坐标,从重心坐标(b1,b2,b3)到标准3D坐标的转换为:
(b1,b2,b3) <==> b1v1 + b2v2 + b3v3
公式12.21 从重心坐标中计算3D点坐标
重心坐标的和总是1:
b1 + b2 + b3 = 1
b1、b2和b3的值是每个顶点对该点的"贡献"或"权"。图12.19展示了一些点和它们的重心坐标。
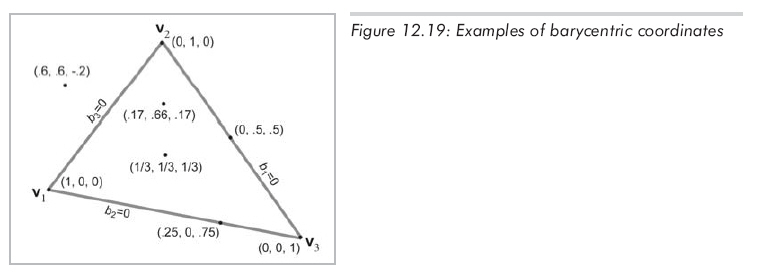
这里应注意以下几点:
(1)三角形三个顶点的重心坐标都是单位向量:
(1, 0, 0) <==> v1
(0, 1, 0) <==> v2
(0, 0, 1) <==> v3
(2)在某顶点的相对边上的所有点的对应重心坐标分量为0。例如,对于所有与v1相对边上的点,b1=0。
(3)不只是三角形内的点,该平面上的所有点都能用重心坐标描述。三角形内点的重心坐标在范围0到1之间变化,三角形外的点至少有一个坐标为负。重心坐标用和原三角形大小相同的块嵌满整个平面,如图12.20所示:
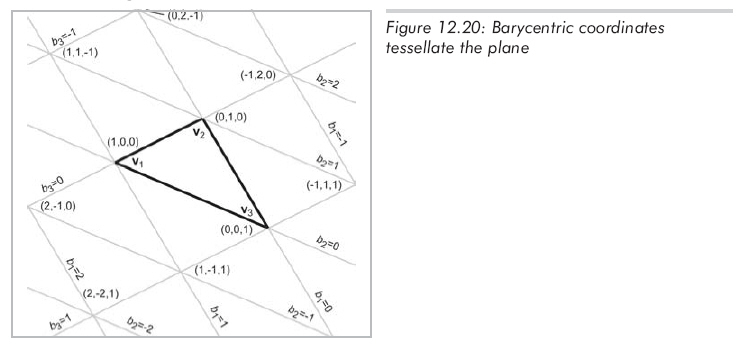
重心坐标空间的本质不同于笛卡尔坐标空间。这是因为重心坐标空间是2D的,但却使用了三个坐标。又因为坐标的和等于1,所以重心坐标空间仅有两个自由度,有一个分量是冗余的。从另一方面说,重心坐标空间中仅用两个数就能完全的描述一个点,用这两个数就可以计算出第三个。
要将一个点从重心坐标空间转换到普通的3D坐标空间,只需要应用公式12.21来计算顶点加权平均值就可以了。而计算2D或3D中任意一点的重心坐标就稍微困难一些。让我们看看怎样在2D中做到这一点。见图12.21,它标出了三个顶点v1、v2、v3和p。我们还标出了三个"子三角形"T1、T2、T3,它们和同样下标的顶点相对。
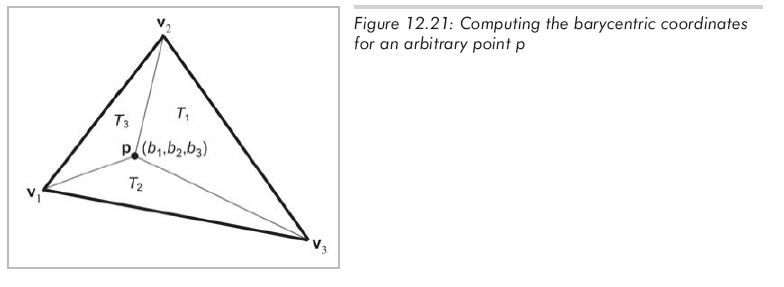
现在,我们知道的是三个顶点和点p的笛卡尔坐标,而任务就是要计算重心坐标b1,b2和b3。根据这些已知条件可以列出三个等式和三个未知数(x,y为顶点)

仔细观察公式12.22,发现每个表达式中的分母相同,并且都等于三角形面积的两倍(根据公式12.20)。还有,对每个重心坐标bi,其分子等于"子三角形"Ti面积的两倍。换据说说:
b1 = A(T1) / A(T)
b2 = A(T2) / A(T)
b3 = A(T3) / A(T)
公式12.23 把重心坐标解释为面积比
注意,即使p在三角形外,这个解释也是成立的,这是因为如果顶点以逆时针方向列出,计算面积的公式将得到一个负值。如果三角形的三个顶点共线,分母上的"子三角形"的面积为0,重心坐标也就没有定义。
计算3D中任意点的重心坐标比在2D中复杂,不能再像以前那样解一个方程组了,因为有三个未知数和四个方程。另一个导致复杂性的地方是p可能不在三角形所在的平面中,这时重心坐标没有意义,但现在我们假设p在三角形所在的平面上。
一种技巧是通过抛弃x、y、z中的一个分量,将3D问题转化到2D中,这和将三角形投影到三个基本平面中某一个上的原理相同。理论上,这是能解决问题的,因为投影面积和原面积成比例。
那么应该抛弃哪个坐标呢?不能总是抛弃某一个,因为如果三角形垂直于某个平面,投影点将共线。如果三角形接近垂直于投影平面,会遇到浮点数精度问题。一种解决方法是挑选投影平面,使得投影面积最大。这可以通过检查平面的法向量做到,我们要抛弃的就是绝对值最大的坐标。例如,法向量为[-1, 0, 0],我们将抛弃顶点p的x分量,把三角形投影到yz平面。下面的代码展示了怎样计算3D中任意点的重心坐标:
Listing 12.3: Computing barycentric coordinates in 3D
bool computeBarycentricCoords3d(
const Vector3 v[3], // vertices of the triangle
const Vector3 &p, // point that we wish to compute coords for
float b[3] // barycentric coords returned here
)
{
// First, compute two clockwise edge vectors
Vector3 d1 = v[1] – v[0];
Vector3 d2 = v[2] – v[1];
// Compute surface normal using cross product. In many cases
// this step could be skipped, since we would have the surface
// normal precomputed. We do not need to normalize it, although
// if a precomputed normal was normalized, it would be OK.
Vector3 n = crossProduct(d1, d2);
// Locate dominant axis of normal, and select plane of projection
float u1, u2, u3, u4;
float v1, v2, v3, v4;
if ((fabs(n.x) >= fabs(n.y)) && (fabs(n.x) >= fabs(n.z)))
{
// Discard x, project onto yz plane
u1 = v[0].y – v[2].y;
u2 = v[1].y – v[2].y;
u3 = p.y – v[0].y;
u4 = p.y – v[2].y;
v1 = v[0].z – v[2].z;
v2 = v[1].z – v[2].z;
v3 = p.z – v[0].z;
v4 = p.z – v[2].z;
}
else if (fabs(n.y) >= fabs(n.z))
{
// Discard y, project onto xz plane
u1 = v[0].z – v[2].z;
u2 = v[1].z – v[2].z;
u3 = p.z – v[0].z;
u4 = p.z – v[2].z;
v1 = v[0].x – v[2].x;
v2 = v[1].x – v[2].x;
v3 = p.x – v[0].x;
v4 = p.x – v[2].x;
}
else
{
u1 = v[0].x – v[2].x;
u2 = v[1].x – v[2].x;
u3 = p.x – v[0].x;
u4 = p.x – v[2].x;
v1 = v[0].y – v[2].y;
v2 = v[1].y – v[2].y;
v3 = p.y – v[0].y;
v4 = p.y – v[2].y;
}
// Compute denominator, check for invalid
float denom = v1 * u2 – v2 * u1;
if (denom == 0.0f)
{
// Bogus triangle - probably triangle has zero area
return false;
}
// Compute barycentric coordinates
float oneOverDenom = 1.0f / denom;
b[0] = (v4*u2 – v2*u4) * oneOverDenom;
b[1] = (v1*u3 – v3*u1) * oneOverDenom;
b[2] = 1.0f – b[0] – b[1];
// OK
return true;
}
另一种计算3D重心坐标的方法基于用向量叉乘计算3D
三角形面积的方法。给出三角形的两个边向量e1和e2,三角形面积为||
e1x
e2|| / 2
。一旦有了整个三角形的面积和三个"
子三角形"的面积,就能计算重心坐标了。
还有一个小小的问题:叉乘的大小对顶点的顺序不敏感。根据定义,叉乘大小总是正的。这种方法不适用于三角形外的点,因为它们至少有一个负的重心坐标。
看看能否找到解决问题的思路。当顶点以"不正确"的顺序列出时,向量叉乘的大小可能会是负值,我们需要一种正确计算的方法。幸运的是,有一种非常简单的方法能做到这一点:点乘。
设c为三角形两个边向量的叉乘,c的大小等于三角形面积的两倍。设有一个单位法向量n,n和c是平行的,因为它们都垂直于三角形所在的平面。当然,它们的方向可能是相反的。两向量的点乘等于它们大小的积再乘以它们夹角的cos值。因为n是单位向量,不管n和c方向相同还是相反,都有:
c . n = ||c|| ||n|| cosθ = ||c|| (1) (±1) = ±||c||
将这个面积除以2,就得到了3D中三角形的"有符号"面积。有了这个技巧,就能利用前一节的结论:bi就是"子三角形"Ti的面积占整个三角形面积的比。如图12.22所示,标出了所有用到的向量。
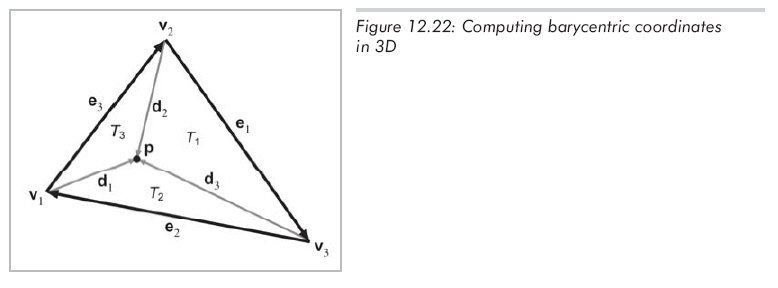
正如你所看到的,每个顶点都有一个向量di,它从vi指向p,列出这些向量满足的方程:

注意到所有的分子和分母中都有n,因此,实际上并不必单位化n。此时,分母为n . n。
这种计算重心坐标的方法比向2D投影的方法用到了更多的标量数学运算。但是它没有分支,并为向量处理器提供了更多的优化机会。因此它在有向量处理器的超标量体系结构中会更快一些。
特殊点
重心是三角形的最佳平衡点,它是三角形三条中线的交点(中线指从顶点到对边中点的连线)。图12.23展示了一个三角形的重心。
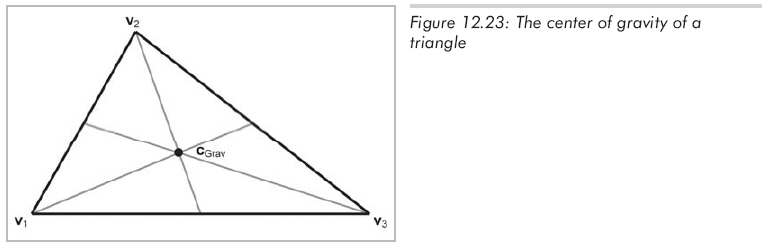
重心是三个顶点的几何均值:
cgrav = (v1+ v2 + v3) / 3
重心坐标为:
(1/3, 1/3, 1/3)
重心也被称作质心。
内心是指到三角形各边距离相等的点。之所以称作内心是因为它是三角形内切圆的圆心,内心是角平分线的交点,如图12.24所示:
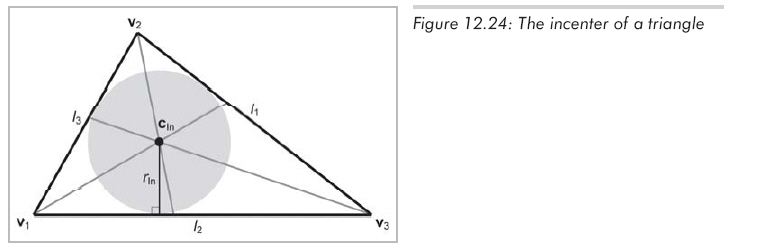
内心的计算:
cin = (L1v1 + L2v2 + L3v3) / p
p = L1 + L2 + L3是三角形的周长,因此,内心的重心坐标为:
(L1/p, L2/p,L3/p)
内切圆的半径可由三角形面积除以周长求得:
rin = A/p
内切圆解决了寻找与三条直线相切的圆的问题。
外心是三角形中到各顶点距离相等的点,它是三角形外接圆的圆心。外心是各边垂直平分线的交点。图12.25展示了一个三角形的外心。
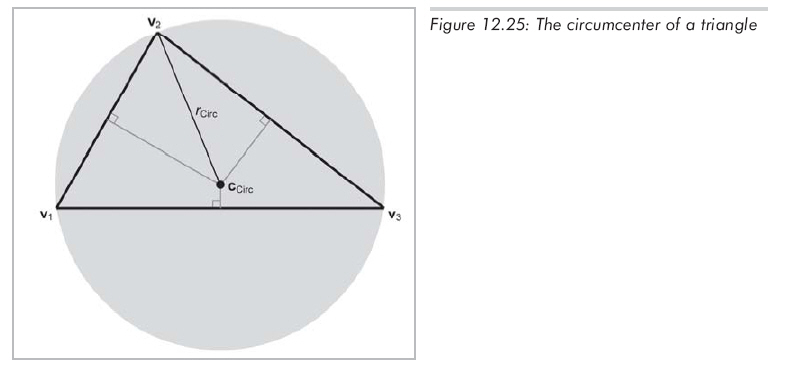
为了计算外心,先定义以下临时变量:
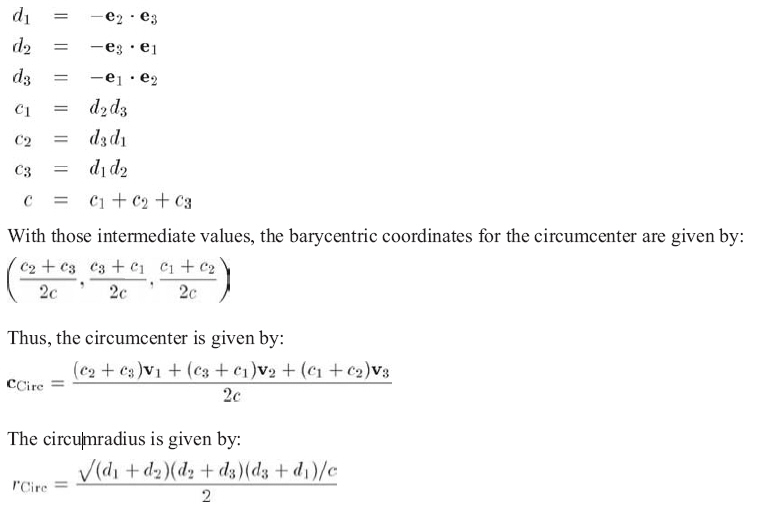
外心和外接圆半径解决了寻找过三个点的圆的问题。