新建网页 1
2D隐式直线上的最近点
考虑2D中的直线L,L由所有满足p . n = d的点p组成。
其中n是单位向量,我们的目标是对任意点q,找出直线L上距q距离最短的点q',它是q投影到L上的结果。让我们画一条经过q平行于L的辅助线M,如图13.1所示。设nM和dM分别为直线方程的法向量和d值。因为L和M平行,所以它们的法向量相等:nM=n。又因为q在M上,所以dM为q.n。
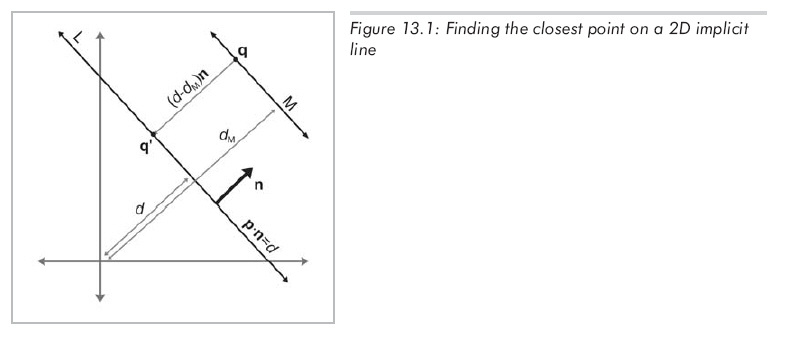
现在可以得知,M到L的有符号距离为:d - dm = d - q . n。这个距离显然等于q于q'之间的距离(如果结果只需要距离而不是q'的值,到这里可以停止计算了)。为了计算q',只需要将q沿n的方向位移一定距离(公式13.1):
q' = q + (d - q . n)n
公式13.1 计算2D隐式直线上的最近点
参数射线上的最近点
考虑在2D或3D中的参数射线R:p(t) = porg + td
其中d是单位向量,参数t在0到L间变化,L是R的长度。 对一给定点q,我们想要找出在R上离q最近的点q'。
这是一个简单的向量到向量的投影问题,设v为porg到q的向量,我们希望得到v在d上的投影,或v平行于d的部分,如图13.2所示:

点乘v . d的结果就是满足p(t)=q'的t值。
t = d . v = d . (q - porg)
q' = p(t) = porg + td = porg + (d . (q - porg))d
公式13.2 计算参数射线上的最近点
实际上,等式p(t)求得了在包含R的直线上距q最近的点。如果t<0或t>L,则p(t)不在R的范围内。这种情况下,R上距q最近的点是原点(如果t<0)或者终点( t>L)。
如果射线的定义是t从0到0变化,d不必是单位向量,那么在计算t值时必须除以d的模:
t = d . (q - porg) / ||d||
平面上的最近点
考虑平面p,其定义为标准的隐式:满足p . n = d的点的集合。
其中n为单位向量,给定一点q,我们想要找到点q',它是q在p上的投影。q'就是p上离q最近的点。
前面已经学过如果计算点到平面上的距离,为了计算q',只要在n的方向上平移一段距离(公式13.3):
q' = q + (d - q .n) . n
公式13.3 计算平面上的最近点
注意到,该式和用于计算在2D中隐式直线上最近点的公式13.1相同。
圆和球上的最近点
考虑2D中的点q和圆心为c、半径为r的圆(下面的讨论也适用于3D中的球体)。我们希望找到点q',它是圆上离q最近的点。
设d为从q指向c的向量,该向量和圆相交于q'。设b为从q指向q'的向量,如图13.3所示:

可以清楚地看出,||b|| = ||d|| - r,因此:
b = ((||d|| - r)/||d||)d
将此位移加到q上,并将它投影到圆上(公式13.4):
q' = q + b = q + ((||d|| - r)/||d||)d
公式13.4 计算圆或球上的最近点
AABB上的最近点
设B是由极值点pmin和pmax定义的AABB。对任意点q都能很容易地计算出B上距离q最近的点q'。所用的方法是按一定的顺序沿着每条轴将q推向B。见程序清单13.1:
Listing 13.1: Computing the closest point in an AABB to a point
if (x < minX)
x = minX;
else if (x > maxX)
x = maxX;
if (y < minY)
y = minY;
else if (y > maxY)
y = maxY;
if (z < minZ)
z = minZ;
else if (z > maxZ)
z = maxZ;
注意,如果q本来就在矩形边界框内部,代码运行的结果将返回原来的点。