AABB与平面的相交性检测
考虑3D中由极值点pmin和pmax定义的AABB和以标准方式定义的平面:p
. n = d,其中n为单位向量,平面与AABB必须处于相同的坐标系中。
一种简单的静态测试方法是,计算矩形边界框顶点和n的点积,通过比较点积和d,来检测边界框的顶点是否完全在平面的一边,或是在另外一边。如果所有点积都大于d,那么整个边界框就在平面的正面所指的一侧;如果所有的点积都小于d,那么整个边界框就在平面的反面所指的一侧。
实际上,不需要检测全部的8个顶点,可以用和变换AABB类似的技巧,例如,如果nx
> 0,点积最小的顶点是x = xmin,点积最大的顶点是x= xmax。如果nx
< 0,则得出的是相反的结论。对ny、nz也有同样的结论。我们计算最小和最大点积的值,如果最小点积大于d或最大点积小于d,说明它们不相交;否则,两个点在平面的两边,说明边界框与平面相交。
接下来进行动态测试,我们假设平面是静止的(以一个移动物体为参考来考虑它们的相交性检测会比较简单)。边界框的位移由单位向量d和长度L定义,和前面一样,先求得点积最大和最小的顶点,并在t=0时作一次相交性检测,如果边界框和平面最初没有相交,那么一定是离平面最近的顶点先接触平面,它可能就是前一步检测出的两个顶点之一。如果只对与平面的"正面"碰撞感兴趣,那么总是使用点积最小的顶点。一旦检测出先接触到平面的顶点,就可以利用射线与平面的相交性测试来解决问题。
cAABB3类实现了AABB与平面的静态、动态相交性检测。
三个平面间的相交性检测
在3D中,三个平面相交于一点,如图13.7所示:
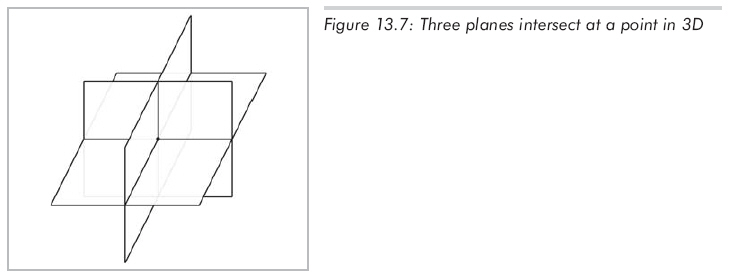
假设三个平面的隐式方程为:
p . n1 = d1
p . n2 = d2
p . n3 = d3
虽然平面的法向量通常被限制为单位向量,但此时这种限制是没有必要的。上面的等式组成了一个有三个方程和三个未知数(交点的x、y、z坐标)的线性方程组。解这个方程组能得到如公式13.7所示的结果:
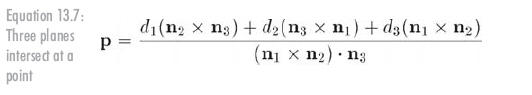
如果任意一对平面平行,那么交点要么不存在,要么不唯一,在这种情况下,公式13.7的分母都为0。
射线和圆/球的相交性检测
这里将讨论2D中射线和圆的相交性检测,检测的方法也适用于3D中射线和球之间的相交性检测,这是因为可以在包含射线和球心的平面中进行检测,从而将3D问题转化为2D问题。(如果射线包含在穿过球心的直线上,那么这个平面就不是唯一的。但这并不是问题,在这种情况下我们能使用任意包含射线和球心的平面来进行计算。)
构图方法见13.8 :
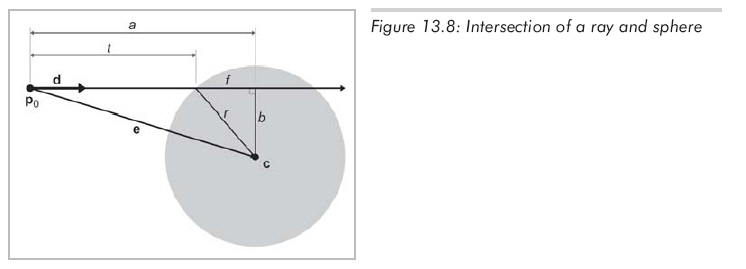
用圆心c和半径r来定义球,射线的定义为:p(t)
= p0 + td
这里,d为单位向量,t从0变化到L,L为射线长度。所要求的是交点处t的值:
t = a - f
a的计算方法如下,设e为从p0指向c的向量:
e = c - p0
现在将e投影到d,这个向量的长度为a,它的计算式为:
a = e . d


两个圆/球的相交性检测
两个球的静态测试是相对比较简单的(这里的讨论对圆也适用,事实上,图13.9中用的就是圆)。考虑由球心c1、c2和半径r1、r2定义的两个球(如图13.9所示)。设d为球心间的距离,很明显,当d
< r1 + r2时它们相交。在实践中通过比较d2
< (r1 + r2)2,可以避免包括计算d在内的平方根运算。
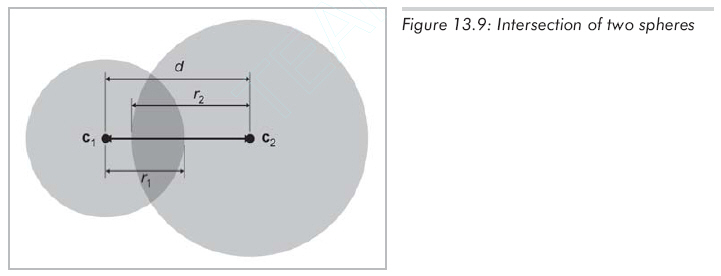
对两个运动的球进行相交性检测要麻烦一些。假设有两个单独的位移向量d1和d2,球与位移向量是一一对应的,它们描述了在所讨论的时间段中球的运动方式。如图13.10所示:
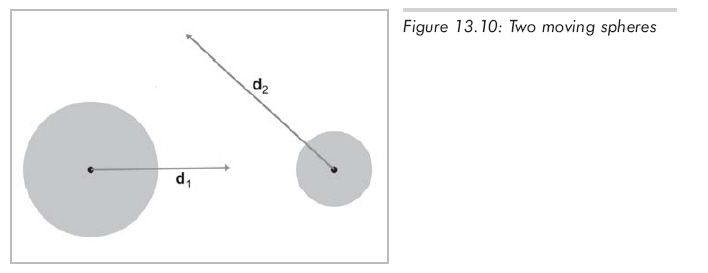
从第一个球的角度来看能够简化这个问题,现在假设这个球是"静止的",另一个球是"运动"的。这给出了单一的位移向量d,它等于原位移向量d2和d1的差d2
- d1,如图13.11所示:
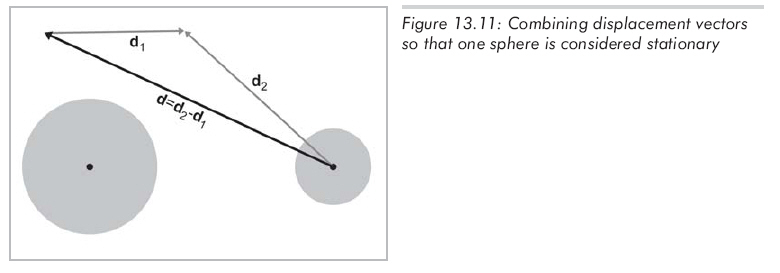
设静止球由球心cs和半径rs定义。运动球的半径为rm,当t=0时,球心为cm。t不再从0变化到1,而是将d单位化,t的取值范围从0到L,L是移动的距离。所以在t时刻运动球的球心为cm
+ td,所要求的是当运动球接触静止球时的t。其中的几何关系如图13.12所示:
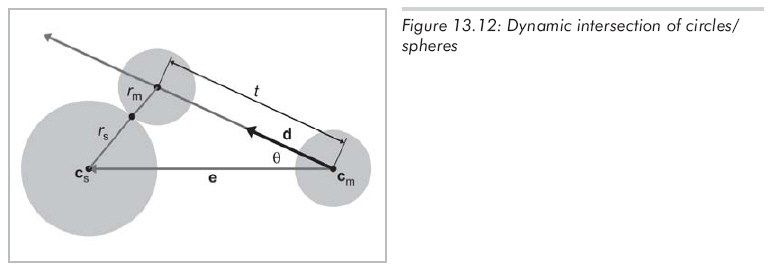

这里有一些重要的注意事项:
(1)如果||e|| < r,则球在t=0时就相交。
(2)如果t<0或t>L,那么在所讨论的时间段内两个球不会发生接触。
(3)如果根号内的值是负的,那么两个球不会相交。
球和AABB的相交性检测
为了进行球和AABB的静态相交性检测,首先找到AABB中距球心最近的顶点。计算该点到球心的距离,并和球的半径比较(实际上,比较的是距离的平方和半径的平方,以避免平方根运算)。如果距离小于半径,那么球和AABB相交。