新建网页 1
球和平面的相交性检测
球和平面的静态检测相对容易一些,可以用公式12.14来计算球心到平面的距离。如果距离小于球半径,那么它们相交。实际上还能作一种更灵活的检测,这种检测把相交分为球完全在平面正面,完全在背面,跨平面等三种情况。仔细分析程序清单13.2:
Listing 13.2: Determining which side of a plane a sphere is on
// Given a sphere and plane, determine which side of the plane
// the sphere is on.
//
// Return values:
//
// < 0 Sphere is completely on the back
// > 0 Sphere is completely on the front
// 0 Sphere straddles plane
int classifySpherePlane(
const Vector3 &planeNormal, // must be normalized
float planeD, // p * planeNormal = planeD
const Vector3 &sphereCenter, // center of sphere
float sphereRadius // radius of sphere
)
{
// Compute distance from center of sphere to the plane
float d = planeNormal * sphereCenter – planeD;
// Completely on the front side?
if (d >= sphereRadius)
return +1;
// Completely on the back side?
if (d <= –sphereRadius)
return –1;
// Sphere intersects the plane
return 0;
}
动态检测要稍微复杂一些。设平面为静止的,球作所有的相对位移。
平面的定义方式一如既往,用标准形式p . n = d,n为单位向量。球由半径r和初始球心位置c定义。球的位移,由单位向量d指明方向,L代表位移的距离。t从0变化到L,用直线方程c+td计算球心的运动轨迹。如图13.13所示:
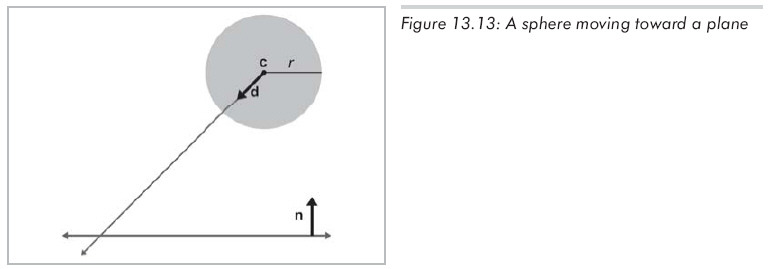
不管在平面上的哪一点上发生相交,在球上的相交点总是固定的,认识到这一点能大大简化问题。用c-rn来计算交点,如图13.14所示:
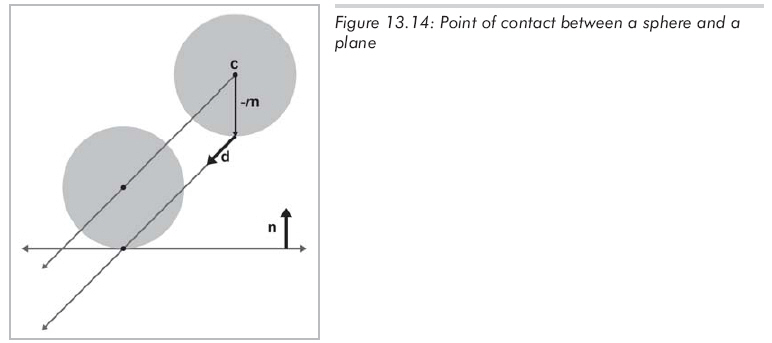
现在我们知道了球上的相交点,就可以利用射线与平面相交性检测的方法,替换掉公式13.6中的p0,得到公式13.9:
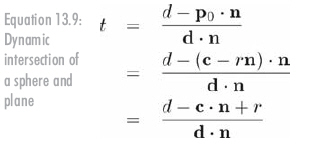
射线和三角形的相交性检测
在图形学和计算几何中射线与三角形的相交性检测是非常重要的。因为缺乏射线和复杂物体间相交性检测的方法,我们通常用三角网格代表(或至少是近似代表)物体表面,再作射线和三角网格的相交性检测。第一步是计算射线和包含该三角形的平面的交点,第二步是通过计算交点的重心坐标,来判断它是否在三角形中。
为了使测试效率尽可能高,要使用下列技巧:
(1)在检测中尽可能地返回负值(没有相交),这称作"提前结束(early out)"。
(2)尽可能地延迟昂贵的数学运算,如除法。有两个原因:第一,如果并不需要昂贵运算的结果,比如说遇到了提前结束的情况,那么执行这些运算的时间就白白浪费了。第二,它给了编译器更多的空间以利用现代处理器的指令管道的优点。在准备除法运算时,它产生执行其他测试的代码(可能导致提前结束)。所以,在执行期间,如果确实需要除法运算的结果,该结果可能已经被计算出来,或至少已经部分被计算出来了。
(3)只检测与三角形正面的相交,这几乎可以节省一半的检测时间。
// Ray-triangle intersection test.
//
// Algorithm from Didier Badouel, Graphics Gems I, pp 390-393
float rayTriangleIntersect(
const Vector3 &rayOrg, // origin of the ray
const Vector3 &rayDelta, // ray length and direction
const Vector3 &p0, // triangle vertices
const Vector3 &p1, // .
const Vector3 &p2, // .
float minT) // closest intersection found so far. (Start with 1.0)
{
// We'll return this huge number if no intersection is detected
const float kNoIntersection = 1e30f;
// Compute clockwise edge vectors.
Vector3 e1 = p1 – p0;
Vector3 e2 = p2 – p1;
// Compute surface normal. (Unnormalized)
Vector3 n = crossProduct(e1, e2);
// Compute gradient, which tells us how steep of an angle
// we are approaching the *front* side of the triangle
float dot = n * rayDelta;
// Check for a ray that is parallel to the triangle or not pointing toward the front face
// of the triangle.
//
// Note that this also will reject degenerate triangles and rays as well. We code this in a
// very particular way so that NANs will bail here. (This does not behave the same as
// "dot >= 0.0f" when NANs are involved.)
if (!(dot < 0.0f))
return kNoIntersection;
// Compute d value for the plane equation. We will use the plane equation with d on the right side:
//
// Ax + By + Cz = d
float d = n * p0;
// Compute parametric point of intersection with the plane containing the triangle, checking at the
// earliest possible stages for trivial rejection.
float t = d – n * rayOrg;
// Is ray origin on the backside of the polygon? Again, we phrase the check so that NANs will bail.
if (!(t <= 0.0f))
return kNoIntersection;
// Closer intersection already found? (Or does ray not reach the plane?)
//
// since dot < 0:
//
// t/dot > minT
//
// is the same as
//
// t < dot * minT
//
// (And then we invert it for NAN checking )
)
if (!(t >= dot * minT))
return kNoIntersection;
// OK, ray intersects the plane. Compute actual parametric point of intersection.
t /= dot;
assert(t >= 0.0f);
assert(t <= minT);
// Compute 3D point of intersection
Vector3 p = rayOrg + rayDelta * t;
// Find dominant axis to select which plane
// to project onto, and compute u's and v's
float u0, u1, u2;
float v0, v1, v2;
if (fabs(n.x) > fabs(n.y))
{
if (fabs(n.x) > fabs(n.z))
{
u0 = p.y – p0.y;
u1 = p1.y – p0.y;
u2 = p2.y – p0.y;
v0 = p.z – p0.z;
v1 = p1.z – p0.z;
v2 = p2.z – p0.z;
}
else
{
u0 = p.x – p0.x;
u1 = p1.x – p0.x;
u2 = p2.x – p0.x;
v0 = p.y – p0.y;
v1 = p1.y – p0.y;
v2 = p2.y – p0.y;
}
}
else
{
if (fabs(n.y) > fabs(n.z))
{
u0 = p.x – p0.x;
u1 = p1.x – p0.x;
u2 = p2.x – p0.x;
v0 = p.z – p0.z;
v1 = p1.z – p0.z;
v2 = p2.z – p0.z;
}
else
{
u0 = p.x – p0.x;
u1 = p1.x – p0.x;
u2 = p2.x – p0.x;
v0 = p.y – p0.y;
v1 = p1.y – p0.y;
v2 = p2.y – p0.y;
}
}
// Compute denominator, check for invalid.
float temp = u1 * v2 – v1 * u2;
if (!(temp != 0.0f))
return kNoIntersection;
temp = 1.0f / temp;
// Compute barycentric coords, checking for out-of-range at each step
float alpha = (u0 * v2 – v0 * u2) * temp;
if (!(alpha >= 0.0f))
return kNoIntersection;
float beta = (u1 * v0 – v1 * u0) * temp;
if (!(beta >= 0.0f))
return kNoIntersection;
float gamma = 1.0f - alpha - beta;
if (!(gamma >= 0.0f))
return kNoIntersection;
// Return parametric point of intersection
return t;
}
还有一个能优化昂贵计算的策略没体现在上述代码中:即预先计算结果。如果像多边形向量这样的值预先被计算出来的话,就可以采用更加优化的策略。
射线和AABB的相交性检测
检测AABB和射线的相交性非常重要,因为根据检测的结果可以避免对更复杂物体的测试。(例如,我们要检测射线与多个由三角网格组成的物体的相交性,可以先计算射线和三角网格的AABB的相交性。有时候可以一次就排除整个物体,而不必去检测这个物体的所有三角形。)
Woo提出一种方法,先判断矩形边界框的哪个面会相交,再检测射线与包含这个面的平面的相交性。如果交点在盒子中,那么射线与矩形边界框相交,否则不存在相交。
cAABB3中rayIntersect()就是用Woo的技术来实现的。
//---------------------------------------------------------------------------
// Parametric intersection with a ray. Returns parametric point
// of intsersection in range 0 1 or a really big number (>1) if no
1 or a really big number (>1) if no
// intersection.
//
// From "Fast Ray-Box Intersection," by Woo in Graphics Gems I, page 395.
//
// See 12.9.11
//---------------------------------------------------------------------------
float AABB3::rayIntersect(const Vector3& rayOrg, // origin of the ray
const Vector3& rayDelta, // length and direction of the ray
Vector3* returnNormal) const // optionally, the normal is returned
{
// We'll return this huge number if no intersection
const float kNoIntersection = 1e30f;
// Check for point inside box, trivial reject, and determine parametric distance to each front face.
bool inside = true;
float xt, xn;
if (rayOrg.x < min.x)
{
xt = min.x - rayOrg.x;
if (xt > rayDelta.x)
return kNoIntersection;
xt /= rayDelta.x;
inside = false;
xn = -1.0f;
}
else if (rayOrg.x > max.x)
{
xt = max.x - rayOrg.x;
if (xt < rayDelta.x)
return kNoIntersection;
xt /= rayDelta.x;
inside = false;
xn = 1.0f;
}
else
xt = -1.0f;
float yt, yn;
if (rayOrg.y < min.y)
{
yt = min.y - rayOrg.y;
if (yt > rayDelta.y)
return kNoIntersection;
yt /= rayDelta.y;
inside = false;
yn = -1.0f;
}
else if (rayOrg.y > max.y)
{
yt = max.y - rayOrg.y;
if (yt < rayDelta.y)
return kNoIntersection;
yt /= rayDelta.y;
inside = false;
yn = 1.0f;
}
else
yt = -1.0f;
float zt, zn;
if (rayOrg.z < min.z)
{
zt = min.z - rayOrg.z;
if (zt > rayDelta.z)
return kNoIntersection;
zt /= rayDelta.z;
inside = false;
zn = -1.0f;
}
else if (rayOrg.z > max.z)
{
zt = max.z - rayOrg.z;
if (zt < rayDelta.z)
return kNoIntersection;
zt /= rayDelta.z;
inside = false;
zn = 1.0f;
}
else
zt = -1.0f;
// Inside box?
if (inside)
{
if (returnNormal != NULL)
{
*returnNormal = -rayDelta;
returnNormal->normalize();
}
return 0.0f;
}
// Select farthest plane - this is
// the plane of intersection.
int which = 0;
float t = xt;
if (yt > t)
{
which = 1;
t = yt;
}
if (zt > t)
{
which = 2;
t = zt;
}
switch (which)
{
case 0: // intersect with yz plane
{
float y = rayOrg.y + rayDelta.y * t;
if (y < min.y || y > max.y)
return kNoIntersection;
float z = rayOrg.z + rayDelta.z * t;
if (z < min.z || z > max.z)
return kNoIntersection;
if (returnNormal != NULL)
{
returnNormal->x = xn;
returnNormal->y = 0.0f;
returnNormal->z = 0.0f;
}
}
break;
case 1: // intersect with xz plane
{
float x = rayOrg.x + rayDelta.x * t;
if (x < min.x || x > max.x)
return kNoIntersection;
float z = rayOrg.z + rayDelta.z * t;
if (z < min.z || z > max.z)
return kNoIntersection;
if (returnNormal != NULL)
{
returnNormal->x = 0.0f;
returnNormal->y = yn;
returnNormal->z = 0.0f;
}
}
break;
case 2: // intersect with xy plane
{
float x = rayOrg.x + rayDelta.x * t;
if (x < min.x || x > max.x)
return kNoIntersection;
float y = rayOrg.y + rayDelta.y * t;
if (y < min.y || y > max.y)
return kNoIntersection;
if (returnNormal != NULL)
{
returnNormal->x = 0.0f;
returnNormal->y = 0.0f;
returnNormal->z = zn;
}
}
break;
}
// Return parametric point of intersection
return t;
}