模型与世界空间
物体最开始由物体空间(和物体相连的坐标空间)来描述,其中常见的信息包括顶点位置和表面法向量。物体空间又称作模型空间或局部空间。
可将坐标从模型空间中转换到世界空间中,此过程称作模型变换。通常,光照计算使用世界空间,但其实使用什么坐标空间无所谓,只要确保几何体与光线在同一空间即可。
摄像机空间
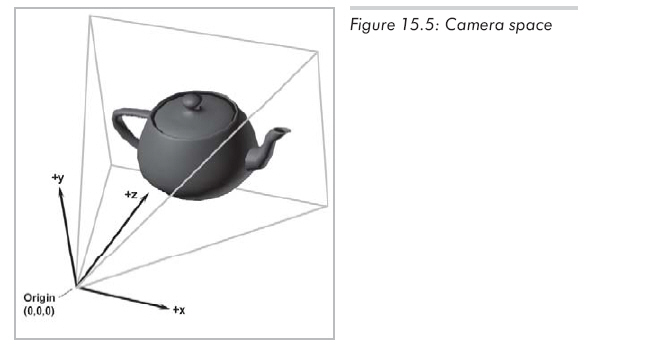
通过视变换,顶点从世界空间变换到摄像机空间,此空间也称作眼睛空间。摄像机空间是原点在投影中心的3D坐标系统,一个轴平行于摄像机拍摄方向且垂直于投影平面,另一个轴由上、下裁剪面相交得到,还有一轴由左、右裁剪面相交得到。如果我们考虑的是透视投影,那么一个轴可视为水平,另一个则可视为垂直的。
左手坐标系中,常约定摄像机朝向+z,而+x和+y指向右和上方向(透视投影情况下)。这是非常直观的,如图15.5所示。右手坐标则指定-z为摄像机朝向。
裁剪空间
从摄像机空间,顶点接着又被变换到裁剪空间,又名标准视体空间(the canonicalview volume
space),该变换对应的矩阵称为裁剪矩阵。
目前为止,顶点还是"纯粹"的3D向量,即它们只有三个坐标值,或者加上第四个分量w,并且w总为1。裁剪矩阵改变了这个现状,它将有用信息放入w中,它主要做两件事:
(1)为透视投影准备向量,由除以w来实现。
(2)规格化x,y,z,使它们可以w比较,用于裁剪。
裁剪矩阵的第一个目的是为透视投影准备向量而将坐标值除以w,4D齐次向量由除以w而对应到3D向量:
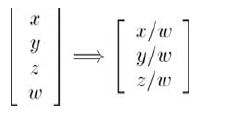
裁剪矩阵的一个目的就是计算正确的w值,以得到正确的投影,我们已经知道如何投影到垂直于z轴且距原点为d的平面(形如z=d的平面)。投影平面在视锥内的矩形部分将映射到屏幕,如果改变d,投影平面将前后移动;在一个真正的摄像机中,这样变化焦距将产生放大、缩小的效果。但对计算机内的投影平面不会如此,增大焦距,像也会变大,但是"底片"(就是投影平面在视锥内的部分)也变大了。因为它们变化的比例一致,所以渲染出的图像不变。因此,计算机图形学中,缩放完全由视锥的形状空间,d值并不重要。所以,我们可以任意选择一个d值并一直使用它,对我们来说最方便的值是d=1。
如果这是裁剪矩阵唯一的目的,即计算正确的w值,那么它可简化如下:
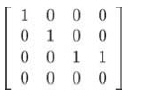
将它乘以形如[x, y, z, 1]的向量再进行透视除法,得到:
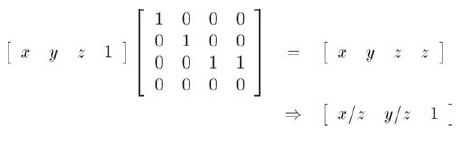
现在已经知道如何用矩阵求得w的值。这里,你也许发现似乎只要除以z就可完成上述工作。没错,的确可以只用z而不涉及w,但4D坐标可以表达更多的摄像机要求,包括一些"奇异"的形式,比如投影面不垂直于摄像机指向;另一个原因是它使得z裁剪(近面和远面裁剪)和x、y裁剪形式一致,从而更好地使用硬件。一般来说,使用齐次坐标4
x 4矩阵更紧凑和优雅。无论如何,多数API都使用它,这才是最重要的。
裁剪矩阵的另一个目的是规格化x、y、z分量,使得6个裁剪面有一致的简单形式。符合下列简单不等式的点在视锥外:
bottom y < -w
top
y > w
left
x < -w
right x >
w
near z < -w
far
z > w
公式15.3 裁剪空间中的视锥
反之,视锥内的定满足下列不等式:
-w ≤ x ≤
w
-w ≤ y ≤
w
-w ≤ z ≤
w
任何不满足这些不等式的点都要被裁减掉。
我们用摄像机的缩放值对x、y进行缩放,从而使上、左、右、下4个剪切面处于正确位置。对于近、远两个剪切面,使得对近剪切面z/w
= -1,远剪切面z/w = 1。
设zoomx、zoomy分别为水平、垂直缩放值,设n、f分别为近、远两个剪切面的距离。下面的矩阵可完成上述计算:

所谓"openGL 风格",是指近裁剪面到远裁剪面的z值在[-w,
+w]之间,其他API(如DirextX)调整z值到区间[0, w]。换言之,如果满足下式,那么点在裁剪面外:
near z < 0
far z > w
而在视锥以内的点则满足:
0 ≤ z ≤
w
此时剪切矩阵稍有不同(公式15.5):
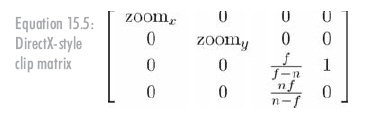
屏幕空间
一旦用视锥完成了几何体裁剪,即可向屏幕空间投影,从而对应于真正的屏幕像素。注意输出窗口不一定占有整个屏幕,只不过,通常情况下希望屏幕坐标系和渲染设备坐标系一致。
显然,屏幕空间是2D的,于是要进行一次3D到2D的映射以得到正确的2D坐标。下列公式概括这一过程:除以w,并调整x、y以映射到如图15.6所示的输出窗口:
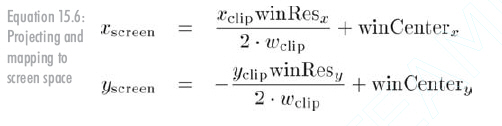
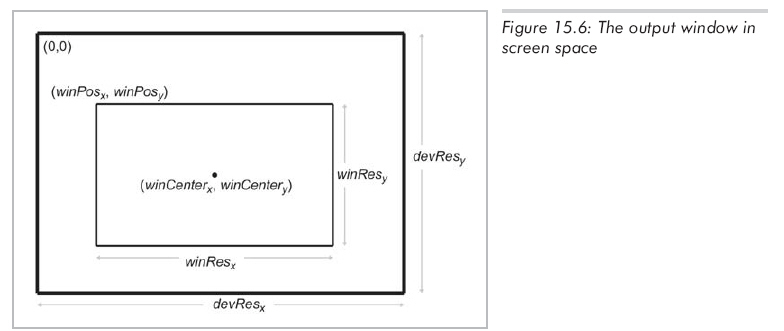
注意y前面的负号,因为裁剪空间中+y向上,而屏幕空间的+y向下。
zscreen和wscreen呢?因为屏幕是2D的,它们并无意义。但也不能简单地丢弃它们,在z缓冲和透视校正中,它们还会有用。