镜面反射分量
标准光照方程的镜面反射分量指由光源直接经物体表面反射入眼睛的光线,如图 15.10:
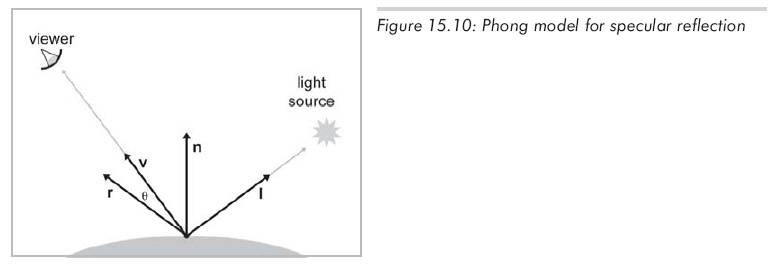
n为表面法向量
v指向观察者
l指向光源,对方向光源,l为定值
r为镜像向量,即l对n镜像之结果
θ为r和v的夹角,由r.v给出,描述镜像的方向性。
镜面反射使物体看上去有光泽,粗糙表面因反射率不高,所以缺乏此类效果。镜面反射的强度取决于物体、光源和观察者。
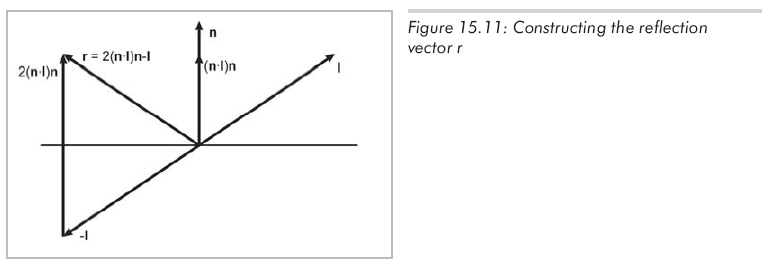
所有向量均为单位向量,如图15.11所示,r由2(n.l)n
- l给出。
下列等式给出镜面反射的Phong模型:
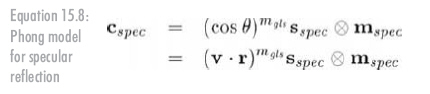
mgls为材料的光泽度,也称作Phong指数,它控制亮斑的范围,小的mgls带来大而平滑的光斑,大的mgls带来小而亮的光斑。完全的反射面,如玻璃,有非常大的mgls----只有反射光进入眼睛,不完全光反射面,如苹果的表面,有较大的亮斑。
另一个有关亮度的值为mspec,即材料的反射颜色,对整个材料来说一般是一个不变的灰度值。mgls控制光斑的大小,mspec控制光斑的强度。强反射面有大的mspec值,粗糙些的表面则有较小的mspec值。如果你愿意,可用一个光泽图控制物体的反射,如同纹理控制物体颜色一样。
sspec是光源的镜面反射颜色,控制光本身的色彩与强度。对于方形聚光灯,此值可能来自投影光照面。sspec常等于光的漫反射颜色sdiff。
图15.12显示了mgls和mspec如何影响物体的镜面反射。图中,mspec从最左列到最右列由黑至白变化,而指数mgls在上方第一行最大,向下递减。注意到,最左面一列的头像看上去一样,因为镜面反射强度为0,对光照没有任何贡献。

如果观察者离物体的距离远大于物体的尺寸,可以仅计算v一次,然后认为它对整个物体是一个常量,同样道理对光源和l也适用。(其实对平行光源,l本身就是固定的。)但由于n是变化的,仍需计算r----这是一个应该尽量避免的计算。Blinn模型通过计算一个稍微不同的角度来避免这个计算。如图15.13所示:
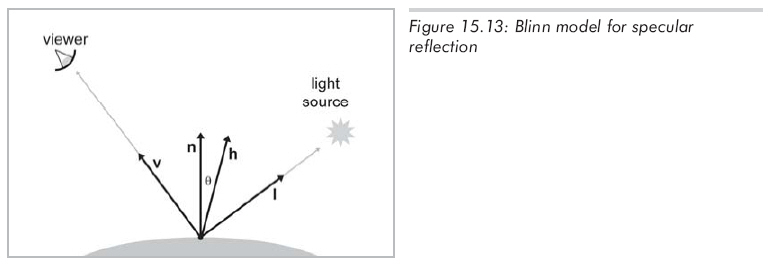
Blinn模型使用h,表示v、l的中间量,由标准化v、l的平均值求得:
h = (v + l) / ||v + l||
公式15.9 Blinn模型中间向量h的计算
Blinn模型和Phong模型一样,只不过θ表示n与h的夹角:
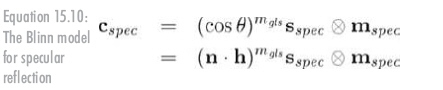
此方程便于硬件的实现,特别是当光源与观察者均远离物体时,此时h被视为常数仅需计算一次。我们忽略的一个细节是有时cosθ小于0,此时简单地令镜面反射为0即可。
漫反射分量
与镜面反射类似,漫反射分量也刻画直接照射物体的光线。漫反射反映的是散开的随机方向上的反射,这是由物体表面的粗糙引起的,相反镜面反射则反映良好的反射。图15.14比较了良好反射表面和粗糙表面。

漫反射不依赖于视点位置,因为它本身就是随机,光源与物体的相对位置反而显得更重要。例如:若假定光线射入眼睛的几率一定,则由于垂直于光线的面在单位面积受光多于一个斜射的面,因为入射眼睛的光线更多,如图15.15所示:

注意上述两种情况中,光线间的垂直距离都相等。(由于错觉,右边的也许显得远些,但量一下,你就发觉实际情况了。)然而,注意右面的图,其命中目标时分得更开些,那么单位面积接受的光线将少些。从图上的示点线可看出左边受光9个单位,而右边只有6个单位,尽管二者面积一样。这正是赤道气候比两极暖和的原因,因为地球是圆的,太阳光在赤道有较直接的照射。
漫反射光服从Lambert法则:反射光强正比于法向量与光线夹角的余弦,用点乘计算余弦,如下:
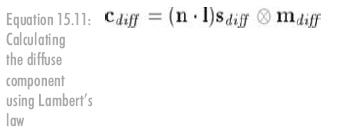
n为表面法向量,l为指向光源的单位向量,mdiff为材料的散射色,即多数人认同的材料颜色。材质多来自纹理图,sdiff为光源散射色,一般和光源镜面色sspec一致。与镜面反射类似,这里也要防止点积出现负值,免得物体从背后透光。
环境光分量
镜面反射和漫反射都是刻画光源经物体反射后进入眼中的光线,但现实世界中,光线也经常在经历多于一次的反射后进入眼睛。好比你在黑暗的厨房打开冰箱,整个房间都会变得亮些,尽管箱门(或你的身体)挡住了大部分直线光。
描述这类反射,我们可用环境光,环境光取决于材质和全局环境光,此时没有涉及任何光源。下面的公式计算环境光:
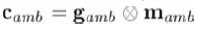
mamb为材质的环境光分量,它总是等于漫反射分量----由纹理图定义,gamb为整个场景的环境光值。