光的衰减
光随距离衰减,所以远离光源的物体会变暗一些。现实世界里,光强度反比于物体和光源距离的平方。
i1 / i2 = d22 / d12
公式15.12
实际光线衰减反比于距离的平方
此处i为光强,d为距离。
实践中,公式15.12并不方便。我们常用另一个简单的基于辐射衰减距离的模型替代,在辐射衰减距离之外,光线将完全衰减为0。通常,可在光线有效射程内使用线性插值表现光随距离d的衰减:
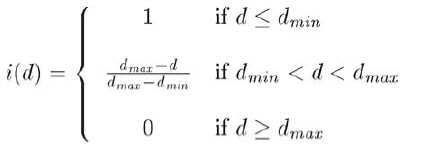
如上,实际有两个辐射衰减距离。在dmin内,光强不衰减;dmin至dmax,光强有1减至0;超出dmax,光强一律为0。dmin控制开始衰减的距离,常设为0,表示光一旦射出即开始衰减;dmax是真正的衰减距离,此距离之外,光完全失效。
距离衰减也适用于点光源和聚光灯(平行光无衰减),聚光灯还多出一个Hotspot辐射衰减半径,表示光亮在光锥边上的衰减。一旦计算出衰减系数i,即可将它乘以镜面反射分量和漫反射分量。记住环境光是不衰减的,这很显然。
光照方程----合成
前面分别讨论了光照方程的各分量,现在是把它们合成到一起的时候了:
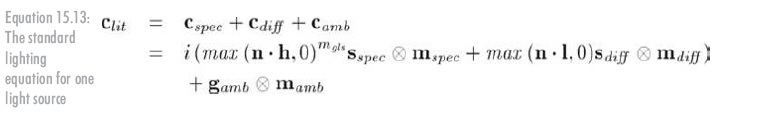
图15.16显示了当光分量独立存在时,各分量的视觉效果:
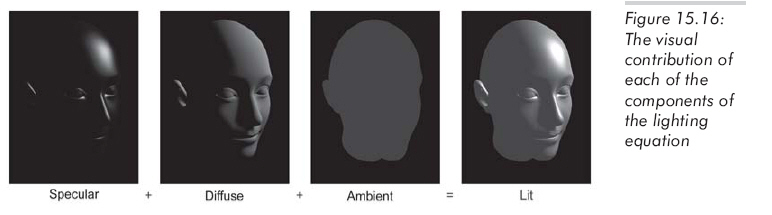
有几点需要注意:耳朵和鼻子一样亮,其实它本应该在头部的影子中。这是采用局部光照的结果,要计算阴影,必须考虑其他高级技术,影子涉及全局光照。前两幅图中,因为没有环境光,头背向光源的部分为全黑。若想照亮物体的背向部分,必须使用环境光,或者在场景中设置更多的光源,使得所有面都能被直接照亮。当只有环境光时,只能看出轮廓。光照是使物体呈现3D外观的重要武器,为了避免这种卡通效果,我们可以使用足够多的光源使场景中的所有表面都被直接照亮。
当有多个光源时,光照方程如何工作?对所有光源求和即可。若Sj表示第j个光源,j从1...n,n是光源个数,光照公式如下:
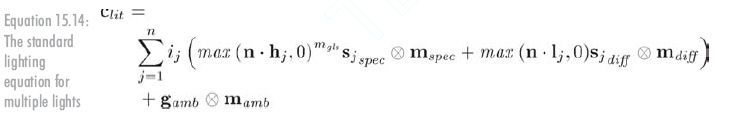
当然因为环境光只有一个,所以不做求和。
雾化
现实中,光线被空气中无数粒子反射与折射。如果单位体积内粒子的浓度足够,则它们是可见的,例如烟、灰尘、雾等。计算机图形学中,上述现象都是通过雾化技术加以模拟的。想象我们正在注视远处的物体,眼睛与物体间的光线受到大量粒子的扰动。一些原来直线传播无法进入眼睛的光线,被那些粒子反射而进入眼睛,这就是我们"看到"空气中粒子的原因。最后的视觉效果上,物体的颜色向雾的颜色偏移,粒子越多,偏移越大。
雾浓度在[0, 1]间取值,控制雾化程度。浓度0表示无雾化,浓度1表示完全雾化,这时像素呈现雾的颜色,最终的颜色值由物体颜色和雾颜色线性插值求得。如何计算雾浓度?前面提到,大气中粒子越多,雾化越显著。然而,如何知道粒子数并转化为雾浓度呢?幸运的是,不必确切知道粒子数,我们用另一个值模拟这个数。粒子数依赖两个因素:场景中的全局武浓度和眼睛与物体间的距离。
眼睛与物体间的距离容易得到。于是,剩下的就是根据这个距离由雾浓度求得像素颜色。如何定义雾的浓度和单位呢?我们不直接定义,而是用一个简化系统。雾浓度由两个距离dmin和dmax控制,像素和眼睛距离小于dmin时无雾化,随着距离的增大,雾化逐渐加重,当距离大于dmax时完全雾化。如公式15.15所示:
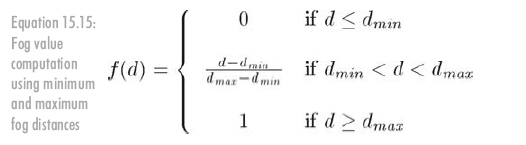
有两点注意事项:
(1)该公式假设雾是空间均匀的,但实际情况并不总是如此。例如,现实世界中,雾常在下方较浓,此模型不能表达这个现象。
(2)距离的定义是可变的。当然,可以用欧式距离,得到球状雾效果,但需要做开方运算。有一种简化是以摄像机空间深度z为距离,从而得到线性雾。它的优点是速度快,但有一个恼人的副作用,某一点雾浓度可能因摄像机朝向的不同而改变,现实世界中这是不可能的。
一旦得到[0, 1]间的雾浓度,像素颜色就可以用如下线性插值公式计算:
cfogged = clit + f(gfog
- clit)
其中:
(1)clit为计算光照后的物体表面颜色
(2)f为公式15.15得出的雾浓度
(3)gfog为全局雾颜色
(4)cfogged为最终效果
为了在场景中得到雾化效果,必须向API说明雾的性质。常需要下列三种信息:
(1)雾化开关,如果要得到雾化效果,必须打开。
(2)雾的颜色,即上式的gfog。
(3)雾化距离,dmin和dmax。