新建网页 1
从欧拉角转换到四元数
为了将角位移从欧拉角转换到四元数,可以使用从欧拉角构造矩阵类似的方法。先将这三个旋转分别转换为四元数,这是一个简单的运算。再将这三个四元数连接成一个四元数。和矩阵一样,有两种情况需要考虑,第一种是惯性 -- 物体四元数,第二种是物体-- 惯性四元数。因为它们互为共轭关系,所以我们只推导惯性--物体四元数。
设欧拉角为变量h、p、b,设h、p、b分别绕轴y、x、z旋转的四元数。记住,使用负旋转量,因为它们指定坐标系中的旋转角度。
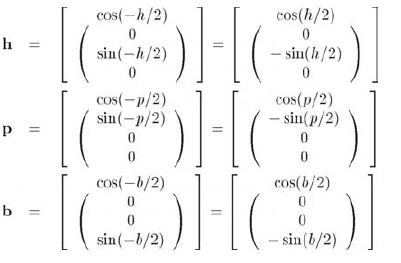
用正确的顺序连接它们得到公式10.24:
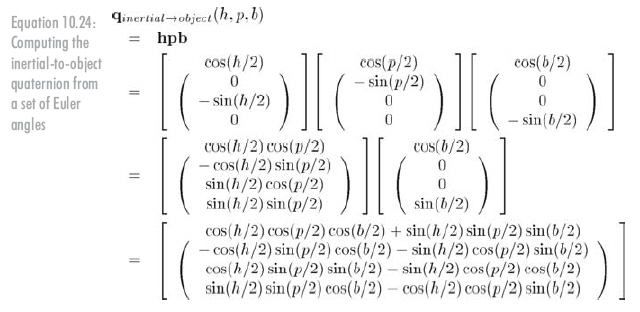
(记住,四元数乘法定义是按旋转的顺序从左向右乘。)
物体--惯性四元数是惯性--物体四元数的共轭,见公式10.25:
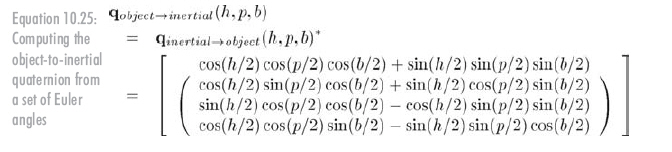
从四元数转换到欧拉角
根据前面的公式发现:


现在可以将它直接转换到代码中,如程序清单10.5所示,它能把惯性--物体四元数转换成欧拉角。
Listing 10.5: Converting an inertial-to-object quaternion to Euler angles
// Use global variables for input and output
float w,x,y,z;
float h,p,b;
// Extract sin(pitch)
float sp = –2.0f * (y*z + w*x);
// Check for Gimbal lock, giving slight tolerance for numerical imprecision
if (fabs(sp) > 0.9999f) {
// Looking straight up or down
p = 1.570796f * sp; // pi/2
// Compute heading, slam bank to zero
h = atan2(–x*z – w*y, 0.5f – y*y – z*z);
b = 0.0f;
} else {
// Compute angles
p = asin(sp);
h = atan2(x*z – w*y, 0.5f – x*x – y*y);
b = atan2(x*y – w*z, 0.5f – x*x – z*z);
}
将物体--惯性四元数转换到欧拉角,所用的代码和上面非常类似。只是将x
、y
、z
值变负,因为物体--惯性四元数是惯性--物体四元数的共轭。
Listing 10.6: Converting an object-to-inertial quaternion to Euler angles
// Extract sin(pitch)
float sp = –2.0f * (y*z – w*x);
// Check for Gimbal lock, giving slight tolerance for numerical imprecision
if (fabs(sp) > 0.9999f) {
// Looking straight up or down
p = 1.570796f * sp; // pi/2
// Compute heading, slam bank to zero
h = atan2(–x*z + w*y, 0.5f – y*y – z*z);
b = 0.0f;
} else {
// Compute angles
p = asin(sp);
h = atan2(x*z + w*y, 0.5f – x*x – y*y);
b = atan2(x*y + w*z, 0.5f – x*x – z*z);
}