新建网页 1
我们使用D3DXMatrixLookAtLH函数来计算视图空间变换矩阵。这个函数对于在固定位置布置和对准摄像机是非常好用的,不过它的用户接口对于要响应用户输入来实现摄像机移动就不那么好用了。这就激发我们用我们自己的方法来解决,这里我们展示了怎样实现一个Camera类,它使我们能够比D3DXMatrixLookAtLH函数更好地操作摄像机,并且可以用来作为飞行模拟摄像机和第一人称视角摄像机。
我们定义一个相对于世界坐标系的位置和摄像机的方向,这里使用四个摄像机向量:right vector , up vector,look vector 以及 position vector,如图12.1所示。这些向量用来为摄像机定义一个坐标系来描述在世界坐标中的对应关系。因为 right ,up 和 look 向量定义了摄像机在世界中的方向,我们有时把它们三个向量一起称为方向向量(orientation vectors)。方向向量必须被标准化。假如彼此互相垂直且都是单位长度,那么我们就称它们是正交标准化向量。我们做这些限制是因为等一会儿我们要将方向向量插入到一个行矩阵中。因为行向量是正交标准化的,所以该矩阵也就是正交矩阵。回忆一下,正交矩阵有一个特性就是它的逆矩阵等于它的转置矩阵。
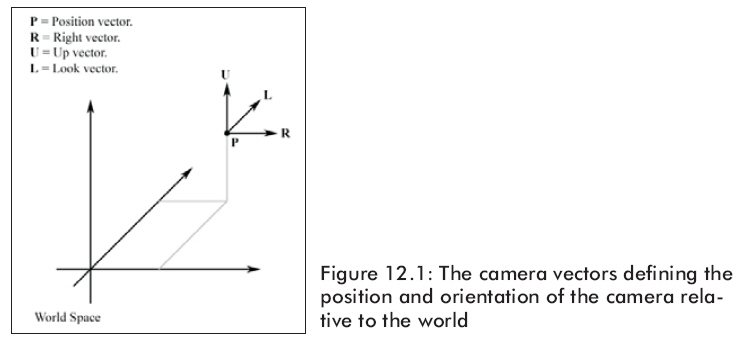
有了这四个向量来描述摄像机,我们的摄像机就能够按照下面六种方式变化了:
围绕right向量旋转(pitch倾斜)
围绕up向量旋转(yaw偏航)
围绕look向量旋转(roll滚转)
沿着right向量平移(strafe)
沿着up向量飞行(fly)
沿着look向量移动(move)
通过这六种操作,我们能够沿着三个轴移动以及饶着三个轴旋转,这给了我们一个六度的自由。下面的Camera类定义了我们要的描述数据以及想要的方法:
enum eCameraType { LAND_OBJECT, AIR_CRAFT };
class cCamera
{
private:
eCameraType m_camera_type;
D3DXVECTOR3 m_right;
D3DXVECTOR3 m_up;
D3DXVECTOR3 m_look;
public:
D3DXVECTOR3 m_pos;
public:
cCamera();
cCamera(eCameraType camera_type);
~cCamera() { };
void strafe(float units); // left/right
void fly(float units); // up/down
void walk(float units); // forward/backward
void pitch(float angle); // rotate on right vector
void yaw(float angle); // rotate on up vector
void roll(float angle); // rotate on look vector
void get_view_matrix(D3DXMATRIX* v);
void set_camera_type(eCameraType camera_type);
void get_right(D3DXVECTOR3* right);
void get_up(D3DXVECTOR3* up);
void get_look(D3DXVECTOR3* look);
};
在类中我们定义了一个还没有讨论的eCameraType枚举类型。目前,我们的摄像机支持两种摄像机模式,LANDO_BJECT模式和AIR_CRAFT模式。AIR_CRAFT模式允许我们在空间中完全自由的移动。不过,在有些游戏中,比如第一人称设计游戏,人是不能飞的;因此我们必须限制它在某些轴上的运动。指定为LAND_OBJECT模式的摄像机就限制了这些。
12.2.1计算视图矩阵
我们现在演示怎样根据摄像机向量来计算视图矩阵变换的。让 p = (px,py,pz),r = (rx,ry,rz),u = (ux,uy,uz)以及 d = (dx,dy,dz)分别表示 position, right, up 以及 look 向量。
视图空间变换是指在世界坐标系中进行几何变换以便将照相机平移变换到坐标系的原点并把它的方向旋转至朝向Z轴的正方向(如图12.2)。
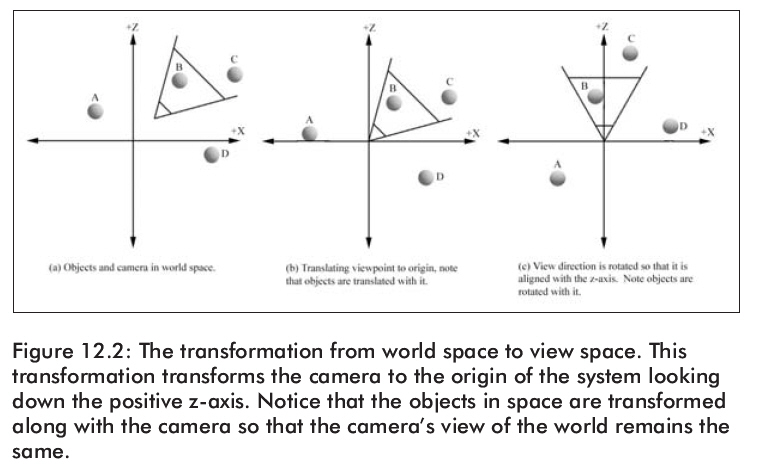
因此,我们希望有一个象这样的变换矩阵V:
pV = (0, 0, 0)—矩阵V能将摄像机移动到原点。
rV = (1, 0, 0)—矩阵V能将摄像机的right向量与世界坐标系中的x轴对齐。
uV = (0, 1, 0)—矩阵V能将摄像机的up向量与世界坐标系中的y轴对齐。
dV = (0, 0, 1)—矩阵V能将摄像机的look向量与世界坐标系中的z轴对齐。
我们能将变换任务分为两个部分:1)平移部分,将摄像机的位置移动到原点;2)旋转部分,将摄像机的方向向量与世界坐标系的轴对齐。
12.2.1.1 第一部分:平移
平移只需要利用 –p就可简单地将 p 移动到原点,因为 p–p=0。因此我们能够用下面的矩阵来描述视图变换中的平移部分:
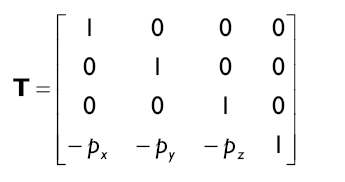
12.2.1.2 第二部分:旋转
矫正摄像机的三个方向向量使其与世界坐标系的轴对齐需要更多的工作。我们需要一个3*3的旋转矩阵A,它能将right,up和look分别与x-,y-以及z轴对齐。这个矩阵将满足如下三个等式:
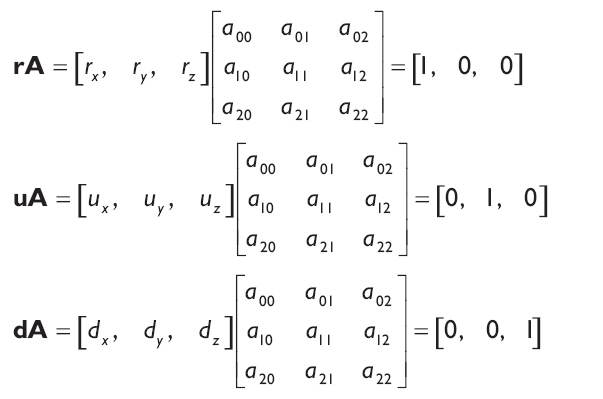
注意:我们在这里使用3*3矩阵来工作是因为现在不需要额外的信息来表现旋转。等一下我们将它增加到常用的4*4矩阵。
因为这三个等式都有一个相同系数矩阵A ,所以我们能够把它们合在一起。我们把它们从新写到一起来:
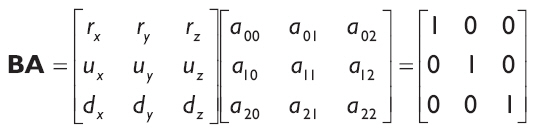
求A有很多方法,但是我们知道A是B逆矩阵因为BA = BB-1 = I。因为B 是一个正交矩阵(它的行向量是正交标准化的),我们知道它的逆矩阵就是它的转置矩阵。因此,将方向向量和世界坐标系中的坐标轴对齐的变换如下:
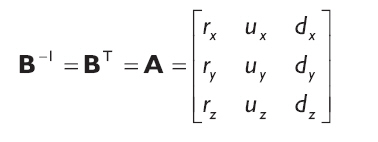
12.2.1.3 将两部分合并
最后,将A增加为4*4矩阵,同时将平移部分合并到旋转部分形成的视图变换矩阵V:
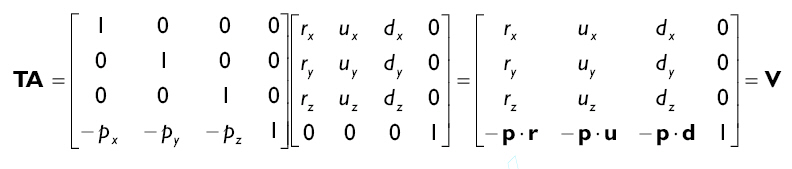
我们在cCamera::get_view_matrix方法中建立这个矩阵:
void cCamera::get_view_matrix(D3DXMATRIX* v)
{
// keep camera's axis orthogonal to each other
D3DXVec3Normalize(&m_look, &m_look);
D3DXVec3Cross(&m_up, &m_look, &m_right);
D3DXVec3Normalize(&m_up, &m_up);
D3DXVec3Cross(&m_right, &m_up, &m_look);
D3DXVec3Normalize(&m_right, &m_right);
// build the view matrix
float x = -D3DXVec3Dot(&m_right, &m_pos);
float y = -D3DXVec3Dot(&m_up, &m_pos);
float z = -D3DXVec3Dot(&m_look, &m_pos);
(*v)(0, 0) = m_right.x; (*v)(0, 1) = m_up.x; (*v)(0, 2) = m_look.x; (*v)(0, 3) = 0.0f;
(*v)(1, 0) = m_right.y; (*v)(1, 1) = m_up.y; (*v)(1, 2) = m_look.y; (*v)(1, 3) = 0.0f;
(*v)(2, 0) = m_right.z; (*v)(2, 1) = m_up.z; (*v)(2, 2) = m_look.z; (*v)(2, 3) = 0.0f;
(*v)(3, 0) = x; (*v)(3, 1) = y; (*v)(3, 2) = z; (*v)(3, 3) = 1.0f;
}
你可能想知道方法中前面几行代码是干什么的。在几次旋转后,摄像机的方向向量可能变的不相互垂直了。因此,每当该函数被调用时,我们根据look向量重新计算up和right向量,使它们保持相互垂直。新的up向量是这样计算的up = look × right。 接着新的right向量是这样计算的right = up × look