[转载]随机数产生原理及应用
原创作者:EmilMatthew
摘要 :
本文简述了随机数的产生原理,并用 C 语言实现了迭代取中法,乘同余法等随机数产生方法,同时,还给出了在符合某种概率分布的随机变量的产生方法。
关键词 : 伪随机数产生,概率分布 , 正态随机数 , 泊松随机数 , 高斯随机数
1 前言 :
在用计算机编制程序时,经常需要用到随机数,尤其在仿真等领域,更对随机数的产生提出了较高的要求,仅仅使用 C 语言类库中的随机函数已难以胜任相应的工作。
用投色子计数的方法产生真正的随机数 , 但电脑若也这样做 , 将会占用大量内存 ; 用噪声发生器或放射性物质也可产生真正的随机数 , 但不可重复 .
而用数学方法产生最适合计算机 , 这就是周期有限 , 易重复的 ” 伪随机数 ”
注 : 这里生成的随机数所处的分布为 0-1 区间上的均匀分布。不是 0-1 区间怎么办 ? 除以 (high-low), 再加上 low 不就行了 . 我们需要的随机数序列应具有非退化性,周期长,相关系数小等优点。
2.1 迭代取中法: ( 鄙视它 )
这里在迭代取中法中介绍平方取中法 , 其迭代式如下 :
Xn+1=(Xn^2/10^s)(mod 10^2s)
Rn+1=Xn+1/10^2s
其中, Xn+1 是迭代算子,而 Rn+1 则是每次需要产生的随机数 。
第一个式子表示的是将 Xn 平方后右移 s 位,并截右端的 2s 位。
而第二个式子则是将截尾后的数字再压缩 2s 倍,显然 :0=<Rn+1<=1.
迭代取中法有一个不良的性就是它比较容易退化成 0.
实现 : 网上一大把 , 略 .
2.2 乘同余法:
乘同余法的迭代式如下 :
Xn+1=Lamda*Xn(mod M) (Lamda 即参数λ )
Rn+1=Xn/M
各参数意义及各步的作用可参 2.1
当然,这里的参数的选取至关重要 .
经过前人检验的两组性能较好的素数取模乘同余法迭代式的系数为 :
1 ) lamda=5^5,M=2^35-31
2 ) lamda=7^5,M=2^31-1
实现 : 请注意,这里一定要用到 double long, 否则计算 2^32 会溢出
2.3 混合同余法: C++ 中的 rand() 就是这么实现的 , 伪随机 , 故使用前一定要加 srand() 来随机取种 , 这样每次实验结果才不会相同 .
混合同余法是加同余法和乘同余法的混合形式 , 其迭代式如下 :
Xn+1=( Lamda*Xn+C )%M
Rn+1=Xn/M
经前人研究表明,在 M=2^q 的条件下,参数 lamda,miu,X0 按如下选取,周期较大,概率统计特性好 :
Lamda=2^b+1,b 取 q/2 附近的数
C=(1/2+sqrt(3))/M
X0 为任意非负整数
它的一个致命的弱点,那就是随机数的生成在某一周期内成线性增长的趋势,显然,在大多数场合,这种极富“规律”型的随机数是不应当使用的。
实现 :
1  double _random( void )
double _random( void )
2 

 {
{
3  int a;
int a;
4  double r;
double r;
5 
6  a = rand() % 32767 ;
a = rand() % 32767 ;
7  r = (a + 0.00 ) / 32767.00 ;
r = (a + 0.00 ) / 32767.00 ;
8 
9  return r;
return r;
10 
11  }
}
3连续型随机变量的生成:
3.1 反函数法 : 又叫反变换法 , 记住 , 它首先需要使用均匀分布获得一个 (0,1) 间随机数 , 这个随机数相当于原概率分布的 Y 值 , 因为我们现在是反过来求 X. 哎 , 听糊涂了也没关系 , 只要知道算法怎么执行的就行 .
采用概率积分变换原理 , 对于随机变量 X 的分布函数 F(X) 可以求其反函数,得 : 原来我们一般面对的是概率公式 Y=f(X). 现在反过来 , 由已知的概率分布或通过其参数信息来反求 X.
Xi=G(Ri)
其中 ,Ri 为一个 0-1 区间内的均匀分布的随机变量 .
F(X) 较简单时,求解较易,当 F(X) 较复杂时,需要用到较为复杂的变换技巧。
可能你没明白 , 看 3.1.1 的例子就一定会明白 .
3.1.1 平均分布 :
已知随机变量密度函数为 :
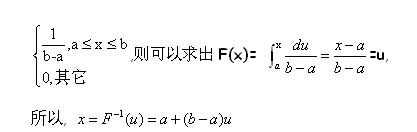
3.1.2 指数分布 :
指数分布的分布函数为 :
x<0 时 ,F(x)=0 ; x>=0,F(x)=1-exp(-lamda*x)
利用反函数法,可以求得 : x=-lnR/lamda( 怎么来的别问 )
3.2 正态分布随机变量的生成 :
正态分布在概率统计的理论及应用中占有重要地位,因此,能产生符合正态分布的随机变量就在模拟一类的工作中占有相当重要的地位。
下面介绍两种方法。
3.2.1
经过一定的计算变行,符合二维的正态分布的随机变量的生成可按下面的方法进行:
1) 产生位于 0-1 区间上的两个随机数 r1 和 r2.
2) 计算 u=2*r1-1,v=2*r2-1 及 w=u^2+v^2
3) 若 w>1 ,则返回 1)
4) x=u[(-lnw)/w]^(1/2) ( 怎么来的别问 )
y=v[(-lnw)/w]^(1/2)
如果为 (miu,sigma^2) 正态分布 , 则按上述方法产生 x 后, x’=miu+sigma*x
由于采用基于乘同余法生成的 0-1 上的随机数的正态分布随机数始终无法能过正态分布总体均值的假设检验。而采用 C 语言的库函数中的随机数生成函数 rand() 来产生 0-1 上的随机数,效果较为理想。
3.2.2 利用中心极限定理生成符合正态分布的随机量:
根据独立同分布的中心极限定理,有 :
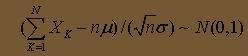
这里,其实只要取 n=12 (这里,亦即生成 12 个 0-1 上的随机数序列)就会有比较好的效果。
经验证,用该种方法生成生的随机数序列同样能比较好的符合正态分布特性。
由于生成的都是标准正态分布,所以,当需要生成 N(a,b) 的正态分布随机量时,根据正态分布的线性变换特性,只要用 x=a*x0+b 即可。(其中, x0 表示生成的符合 N(0,1) 分布的正态随机变量。方法 3.1 亦是如此)
实现 :


 1 : double _sta( double mu, double sigma) // 利用中心极限定理生成
1 : double _sta( double mu, double sigma) // 利用中心极限定理生成

 2
2  {
{
 3 int i;
3 int i;
 4 double r,sum = 0.0 ;
4 double r,sum = 0.0 ;
 5
5

 6 if (sigma <= 0.0 )
6 if (sigma <= 0.0 )  { printf( " Sigma<=0.0 in _sta! " ); exit( 1 ); }
{ printf( " Sigma<=0.0 in _sta! " ); exit( 1 ); }
 7 for (i = 1 ;i <= 12 ;i ++ )
7 for (i = 1 ;i <= 12 ;i ++ )
 8 sum = sum + _random();
8 sum = sum + _random();
 9 r = (sum - 6.00 ) * sigma + mu;
9 r = (sum - 6.00 ) * sigma + mu;
 10
10
 11 return r;
11 return r;
 12
12
 13 }
13 }
 14
14

 1 double _sta2( double mu, double sigma) // 利用反函数法公式x=u[(-lnw)/w]^(1/2)
1 double _sta2( double mu, double sigma) // 利用反函数法公式x=u[(-lnw)/w]^(1/2)

 2
2  {
{
 3 double r1,r2;
3 double r1,r2;
 4
4
 5 r1 = _random();
5 r1 = _random();
 6 r2 = _random();
6 r2 = _random();
 7
7
 8 return sqrt( - 2 * log(r1)) * cos( 2 * M_PI * r2) * sigma + mu ;
8 return sqrt( - 2 * log(r1)) * cos( 2 * M_PI * r2) * sigma + mu ;
 9
9
 10 }
10 }
4 离散型随机变量的生成 :
离散型随机变量的生成主要是希望得到在已知 X 符合某类分布的条件下,生成相应的 X 。
4.1 符合泊松分布的随机变量的生成 :
这里,采用 ” 上限拦截 ” 法进行测试 ,我看了不懂 , 希望有人帮我分析一下 , 从数学角度帮我分析一下,谢谢!
基本的思想是这样的:
1 )在泊松分布中,求出 X 取何值时, p(X=k) 取最大值时,设为 Pxmax.
其时,这样当于求解 f(x)=lamda^k/k! 在 k 取何值时有最大值,虽然,这道题有一定的难度,但在程序中可以能过一个循环来得到取得 f(x) 取最大值时的整数自变量 Xmax 。
2) 通过迭代,不断生成 0-1 区间上的随机数,当随机数 <Pxmax 时,则终止迭代,否则重复 (2)
3) 记录迭代过程的次数,即为所需要得到的符何泊松分布的随机量。
显然,这种方法较为粗糙,在试验的过程中发现:生成的的随机量只能算是近似的服从泊松分布,所以,更为有效的算法还有待尝试。
实现 : 采用 double 至少可以支持 lamda=700 ,即 exp(-700)!=0


 1 const int MAX_VAL = 10000 ;
1 const int MAX_VAL = 10000 ;
 2 double U_Rand( double a, double b ) // 均匀分布
2 double U_Rand( double a, double b ) // 均匀分布

 3
3  {
{
 4 double x = random( MAX_VAL );
4 double x = random( MAX_VAL );
 5 return a + (b - a) * x / (MAX_VAL - 1 );
5 return a + (b - a) * x / (MAX_VAL - 1 );
 6 }
6 }
 7 double P_Rand( double Lamda ) // 泊松分布
7 double P_Rand( double Lamda ) // 泊松分布

 8
8  {
{
 9 double x = 0 ,b = 1 ,c = exp( - Lamda ),u;
9 double x = 0 ,b = 1 ,c = exp( - Lamda ),u;

 10 do
10 do  {
{
 11 u = U_Rand( 0 , 1 );
11 u = U_Rand( 0 , 1 );
 12 b *= u;
12 b *= u;
 13 if ( b >= c )
13 if ( b >= c )
 14 x ++ ;
14 x ++ ;
 15 } while ( b >= c );
15 } while ( b >= c );
 16 return x;
16 return x;
 17 }
17 }
为防止lamda过大而溢出,故应该自己来写一个浮点类,我不懂,摘抄的.
下面是一个简单的浮点类,还有一个用该浮点类支持的 Exp ,以及简单的测试
可以不用位域,而只用整数来表示 double ,然后用移位来进行转换
这里用位域只是为了简单和明了(看清 double 的结构)


 1 #include < math.h >
1 #include < math.h >
 2 #include < iostream.h >
2 #include < iostream.h >
 3
3
 4 const int nDoubleExponentBias = 0x3ff ;
4 const int nDoubleExponentBias = 0x3ff ;
 5
5
 6 typedef struct
6 typedef struct

 7
7  {
{
 8 unsigned int uSignificand2 : 32 ;
8 unsigned int uSignificand2 : 32 ;
 9 unsigned int uSignificand1 : 20 ;
9 unsigned int uSignificand1 : 20 ;
 10 unsigned int uExponent : 11 ;
10 unsigned int uExponent : 11 ;
 11 unsigned int uSign : 1 ;
11 unsigned int uSign : 1 ;
 12 } DOUBLE_BIT;
12 } DOUBLE_BIT;
 13
13
 14 typedef union
14 typedef union

 15
15  {
{
 16 double lfDouble;
16 double lfDouble;
 17 DOUBLE_BIT tDoubleBit;
17 DOUBLE_BIT tDoubleBit;
 18 } DOUBLE;
18 } DOUBLE;
 19
19
 20
20
 21 class TFloat
21 class TFloat

 22
22  {
{
 23 int m_uSign;
23 int m_uSign;
 24 int m_uExponent;
24 int m_uExponent;
 25 unsigned int m_uSignificand1;
25 unsigned int m_uSignificand1;
 26 unsigned int m_uSignificand2;
26 unsigned int m_uSignificand2;
 27
27
 28
28
 29 public :
29 public :
 30
30
 31 TFloat( void );
31 TFloat( void );
 32 TFloat( const double lfX );
32 TFloat( const double lfX );
 33 TFloat( const TFloat & cX );
33 TFloat( const TFloat & cX );
 34
34
 35 TFloat & operator *= ( const TFloat & cX );
35 TFloat & operator *= ( const TFloat & cX );
 36 bool operator <= ( const TFloat & cX );
36 bool operator <= ( const TFloat & cX );
 37
37
 38 void GetFromDouble( double lfX );
38 void GetFromDouble( double lfX );
 39 double ToDouble( void ); // for test
39 double ToDouble( void ); // for test
 40 } ;
40 } ;

4.2符合二项分布的随机变量的生成:
符合二项分布的随机变量产生类似上限拦截法,不过效果要好许多,这是由二项分布的特点决定的。
具体方法如下:
设二项分布B(p,n),其中,p为每个单独事件发生的概率:
关键算法:
i=0;reTimes=0
while(i<n)
{
temp=myrand();//生成0-1区间上的随机变量
if(temp>1-p)
reTimes++;
i++;
}
显然,直观的看来,这种算法将每个独立的事件当作一个0-1分布来做,生成的0-1区间上的随机数,若小于1-p则不发生,否则认为发生,这样的生成方式较为合理。实验结果也验证了其合理性。
4.3高斯分布随机数:贴一个最经典的程序,看程序大概就知道高斯分布函数的反函数了.
#include <stdlib.h>
#include <math.h>
double gaussrand()
{
static double V1, V2, S;
static int phase = 0;
double X;
if ( phase == 0 ) {
do {
double U1 = (double)rand() / RAND_MAX;
double U2 = (double)rand() / RAND_MAX;
V1 = 2 * U1 - 1;
V2 = 2 * U2 - 1;
S = V1 * V1 + V2 * V2;
} while(S >= 1 || S == 0);
X = V1 * sqrt(-2 * log(S) / S);
} else
X = V2 * sqrt(-2 * log(S) / S);
phase = 1 - phase;
return X;
}
posted on 2006-11-08 18:52
哈哈 阅读(14880)
评论(16) 编辑 收藏 引用