群结构
定理1：若G为一个循环群，则G内每个满足ord(
α)=s的元素
α都是拥有s个元素的循环子群的生成元
证明：
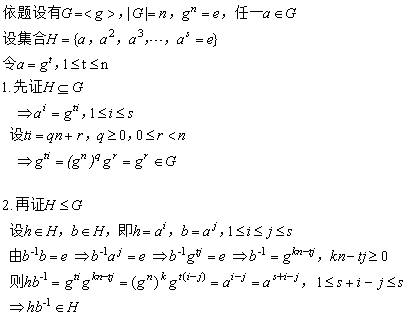定理2：若G为一个阶为n的有限循环群，g为对应的生成元，则对整除n的每个整数k，G都存在一个唯一的阶为k的循环子群H。
这个子群是由g
n/k生成的。H是由G内满足条件
αk=1的元素组成的，且G不存在其它子群
证明：
推论：从上述两定理可知有限循环群、子群及生成元的关系如下
例子：依据上述推论得如下
生成元判定算法
输入：循环群G、某子群的阶k
1）若k=1，则直接输出e。否则转到2）
2）随机从G-{e}中选择一元素x
3）若x
k≠e，则转回2）。否则若k为素数，则跳到5）；若k为合数，则转到4）
4）遍历整除k的真因子d，若x
d=e，则转回2）
5）输出x
posted on 2024-03-20 22:49
春秋十二月 阅读(549)
评论(0) 编辑 收藏 引用 所属分类:
Algorithm