基本函数F(n)=G(n) + H(n);

其中G(n)是从起始点到当前点的距离，H(n)是从当前点到目标点的估计距离。

例如对于一个网格状的路网可以横走和竖走，H(n)就是标准Manhattan距离：

h(n) = D * (abs(n.x-goal.x) + abs(n.y-goal.y))

D是走一步的代价。

对于不同的情况H(n)的选取很关键，H越大运算时间越短但得到最优解的可能性越低

H越小运算时间越长得到最优解的可能性越高。当H为0时就是dijkstra算法。

1)         创建OPEN和CLOSE表。其中OPEN为待评估的点，CLOSE为已经运算评估过的点。其中OPEN使用二叉堆便于排序。

2)         初始化将起始点计算F(n)并加入到OPEN表。

3)         取当前OPEN中的最小F(n)点为当前点，将他从OPEN表中删除,加入到CLOSE表。

4)         计算当前点的所有附近点(即一步能达到的点)

4.1   对于附近点计算cost=当前点的G(n)+当前点到附近点的开销。

4.2   如果附近点已经在OPEN中则比较附近点的G(n)和cost，如果cost小于附近点的G(n)则更新OPEN表中的附近点的G(n)为cost和F(n)，并把它的父节点设为当前点。反之不做操作。

4.3   如果附近点在CLOSE表中则比较附近点的G(n)和cost，如果cost小于附近点的G(n)，则将附近点从CLOSE表中删除并更新该附近点的G(n)和F(n)并加入到OPEN表，并把它的父节点设为当前点。反之不操作。

4.4   如果附近点既不在OPEN表也不在CLOSE表，则计算附近点的G(n),H(n)和F(n)并加入到OPEN表，并把它的父节点设为当前点。

5)         从3步骤开始重新计算直到当前点为目标点。

6)         从目标点开始按父节点给出到起始点的最短路径。

其中的关键是对OPEN表、CLOSE表的数据结构设计。由于OPEN表中存在排序和查找的基本操作，CLOSE表也存在查找的基本操作。

当数据量大时，数据结构的优势体现的非常明显。OPEN表一般都使用二叉堆的形式，CLOSE表则使用简单的数组即可。

实际测试产生一个1366*768 像素通路点和障碍点为1:2的随机网格地图从坐标(100, 100)到(1000, 300)的算路时间(h取Manhattan距离)在5400双核cpu，2g内存下大概为120秒左右。

遗传算法

网上建模实现的方法很多
 第一种 针对网格状地图的遗传算法

1.       将地图抽象成网格，对于不同地形赋不同值，例如高速路标的值可以比辅路低3到4倍。

2.       旋转地图使起点和终点调节成位于同一个纵坐标。

3.       将起点到终点将的像素点划分成几个块。

4.       对于每个块产生随机的基因(即变异的过程)，保证每个块的当前基因位置与前一个基因位置相差小于2个像素点(即2个基因连通)。如图红蓝为2个独立的染色体：

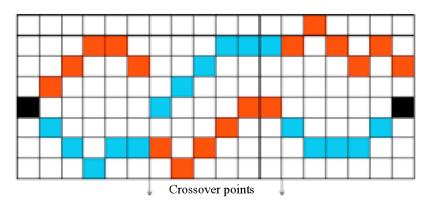
5.       计算所有染色体的适应度。选择最小的2个染色体作为双亲。

6.       对双亲进行随机交配产生子代。当产生的子代形成一条通路时停止。否则返回到第五步。

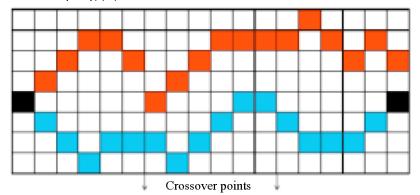
他人的运行结果：

以上算法存在的最大缺陷是当存在的路径垂直于起点和终点的连接线时，无法产生适合的基因，因为该算法产生的基因对于每一个纵坐标是唯一的。

l第二种 针对路网结构的遗传算法

大致思想如下：

1． 针对起点和终点先产生n条连通路径作为原始的种群。

2． 计算每条路径的适应度(一般都以路径的长度为基础作为适应度)。

3． 进行随机交配(前提是双亲必须有交叉点)。这个变化最大随机的好坏决定了整个算法的优劣。

4． 淘汰掉适应度最低的m条道路。

5． 重复2-4步骤。设定结束条件为连续k次遗传的最优解都是同一个或者设定遗传的次数(到例如50次自动结束)。

6． 将适应度最高的作为最终解。

以上算法的难点在于原始种群的产生有一定难度，取小了无法满足交叉条件，取大了耗费运算时间且复杂度提高