本文观点翻译至Ron Gutman和Andrew V.Goldberg的两篇论文。经过实际中国地图测试,对于dijkstra和A*算法均能大大的减少edge探索数目(探索范围没有明显减少,但稀疏度大大提高),能相对与不使用Reach-V剔除90%以上的节点。
定义:
定义顶点reach值:一条通过该顶点的最短路径中的被该点分割的较短那部分路径的长度。
定义顶点reach估计值(reach-v):所有通过该点的最短路径中的reach值的最大值。
举例:
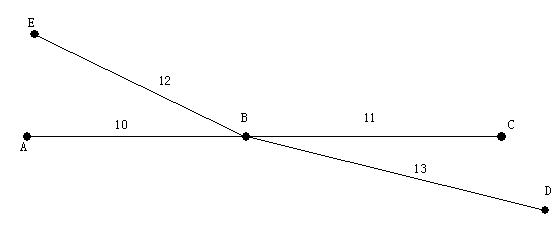
对于如图所示的双向图
reach-v(B) = 12,其余各个顶点的reach-v全为0。
算法中的用法:
以dijkstra为例,假设当前算路的起点终点分别为S,T。当前探索点为V,记m(p)为从S到V的最短路径长度,记d(V,T)为从V到T的欧几里得距离。
如果reach-v(V) < m(p) && reach-v(V) < d(V,T)则排除掉V点(不探索)。
对于A*算法同理,m(p)对应于A*中的G,d(V,T)对应于A*的H。
Reach-V值的计算:
由于对所有节点都做全图的dijkstra规模过于庞大,对于几千万上亿个节点的地图运算时间会达到几年,所以实际中一般都是选取一个合适的Reach-V值上界,以在预处理时间和时间剔除效果间做一个平衡。 以下将着重介绍一种P-Tree思想来对每个节点做dijkstra。P-Tree顾名思义就是对每个节点不做全图的dijkstra,而是设定一个停止条件以产生一棵局部最短路径树。(待续)
posted on 2011-05-13 11:10
saha 阅读(767)
评论(0) 编辑 收藏 引用