Blocks
| Time Limit: 1000MS |
|
Memory Limit: 65536K |
| Total Submissions: 720 |
|
Accepted: 201 |
Description
Panda has received an assignment of painting a line of blocks. Since Panda is such an intelligent boy, he starts to think of a math problem of painting. Suppose there are N blocks in a line and each block can be paint red, blue, green or yellow. For some myterious reasons, Panda want both the number of red blocks and green blocks to be even numbers. Under such conditions, Panda wants to know the number of different ways to paint these blocks.
Input
The first line of the input contains an integer T(1≤T≤100), the number of test cases. Each of the next T lines contains an integer N(1≤N≤10^9) indicating the number of blocks.
Output
For each test cases, output the number of ways to paint the blocks in a single line. Since the answer may be quite large, you have to module it by 10007.
Sample Input
2
1
2
Sample Output
2
6
Source
给定一块有n个点的木块,用四种颜色涂色,其中两种颜色只能用偶数次,求有多少种涂色方法。
一看就知是生成函数,可惜从没用过。小试身手,没想到竟然弄出来了。结果应该是对的,就是不知过程是不是可以这样写。
设四种颜色分别为w,x,y,z,其中y,z只能用偶数次,我的推导过程如下:
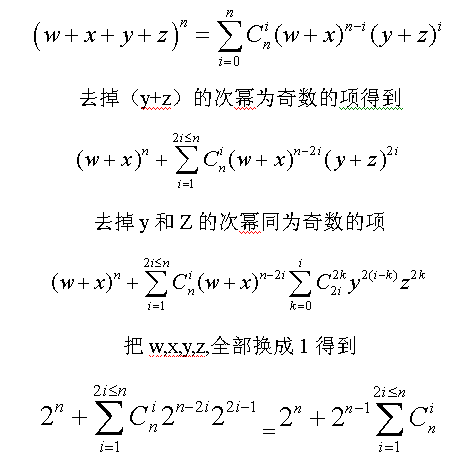
最后得到的公式是(2^( n - 1 ))(2^(n-1)+1)
注意到10007是素数,由费尔马定理,可以先把n-1mod(10007-1),减小计算量,剩下的就是快速取幂了.
 #include <iostream>
#include <iostream>
 using namespace std;
using namespace std;
 const int mod=10007;
const int mod=10007;
 int pow(int n)
int pow(int n)


 {
{
 if(n==0)
if(n==0)
 return 1;
return 1;
 if(n&1)
if(n&1)


 {
{
 return (pow(n-1)<<1)%mod;
return (pow(n-1)<<1)%mod;
 }
}
 else
else


 {
{
 int temp=pow(n>>1);
int temp=pow(n>>1);
 return (temp*temp)%mod;
return (temp*temp)%mod;
 }
}
 }
}

 int main(int argc, char *argv[])
int main(int argc, char *argv[])


 {
{
 int t,n,temp;
int t,n,temp;
 cin>>t;
cin>>t;
 while(t--)
while(t--)


 {
{
 cin>>n;
cin>>n;
 temp=pow((n-1)%(mod-1));
temp=pow((n-1)%(mod-1));
 cout<<(temp*(temp+1))%mod<<endl;
cout<<(temp*(temp+1))%mod<<endl;
 }
}

 return 0;
return 0;
 }
}

//由于近日POJ登不上,上面的代码未曾提交过