以前从没有对O（log N）和O（N）的区别有所正确认识，今日总算知道了。它们的唯一区别就是，N是一亿的时候，log(N)就是不到26，N还是一亿。
http://acm.pku.edu.cn/JudgeOnline/problem?id=3070
PKU的这道题虽然容易，但的确很有意思。我也是第一次用快速幂取模，一用，果然不同凡响。
快速幂取模，其实就是秦九韶算法 取指数。
把n化成二进制形式后，得到一个多项式,写成秦九韶形式，多项式的加就是乘，乘则为指数运算（指数为2）。由于N的二进制位个数为log(n),这样把O（N）的问题化为O（log N）。
.
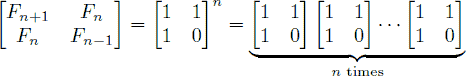//PKU 3070 ,calculate Fibonacci
#include <iostream>
#include<stack>
int FPM(int);//fast-power-modulus function declare
using namespace std;
const int Mod=10000;
int main(int argc, char *argv[])
{
int n=0;
while(scanf("%d",&n))
{
if(n==-1)
break;
printf("%d\n",FPM(n));
}
return 0;
}
int FPM(int n)//fast-power-modulus function
{
int matr[4]={1,0,0,1};//initialize matrix
stack<bool>dec;//stack to store binary digit
while(n)//resolve n to binary digit
{
dec.push(1&n);//get the last binary digit
n>>=1;
}
while(!dec.empty())
{
//matrix square
matr[1]=((matr[0]+matr[3])*matr[1])%Mod;
matr[0]=(matr[0]*matr[0]+matr[2]*matr[2])%Mod;
matr[3]=(matr[3]*matr[3]+matr[2]*matr[2])%Mod;
matr[2]=matr[1];
//matrix multiply,
if(dec.top())
{
matr[0]=(matr[0]+matr[1])%Mod;
matr[1]=(matr[1]+matr[3])%Mod;
matr[3]=matr[2];
matr[2]=matr[1];
}
dec.pop();
}
return matr[1];//matr[1] is the result F[N]
}